Обзор ключевых понятий осевого сечения сферы и шара для лучшего восприятия
Осевое сечение сферы или шара – это важная геометрическая концепция, которая помогает лучше понять, как объекты взаимодействуют с плоскостью. В данной статье мы разберем, что такое осевое сечение, как его правильно интерпретировать и какие полезные советы могут облегчить понимание этой темы с помощью визуальных примеров и подробных объяснений.


Для начала убедитесь, что понимаете разницу между сферой и шаром: шар – это объемная фигура, а сфера – только ее поверхность.

Шарик, катящийся по вращающейся платформе
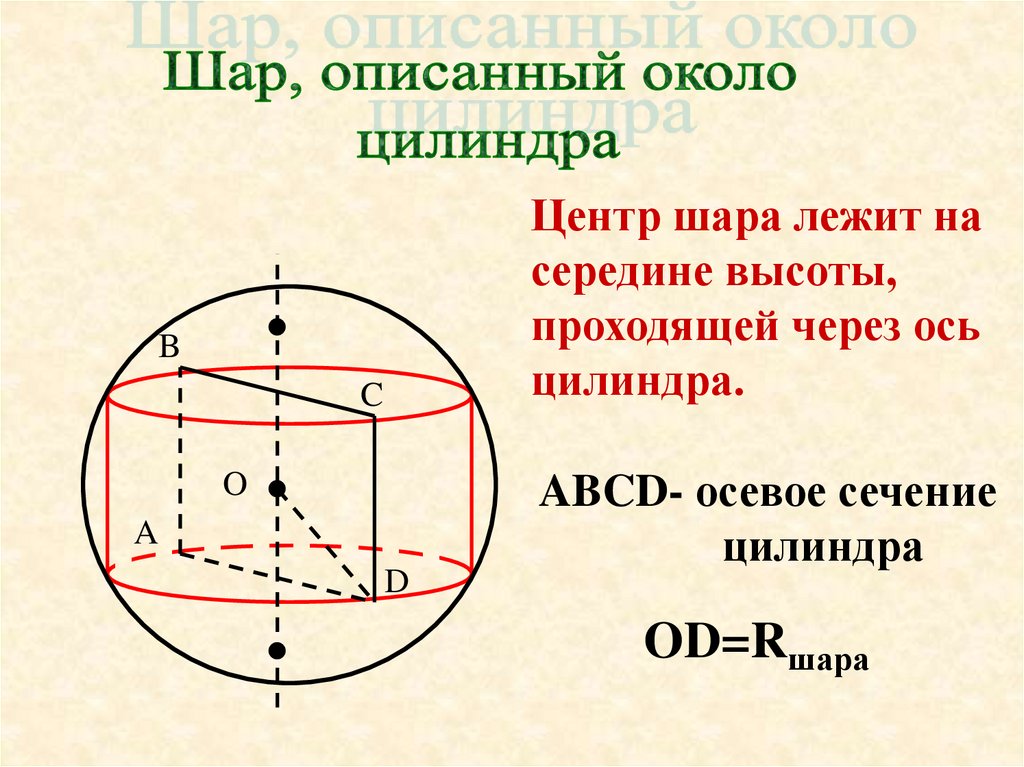
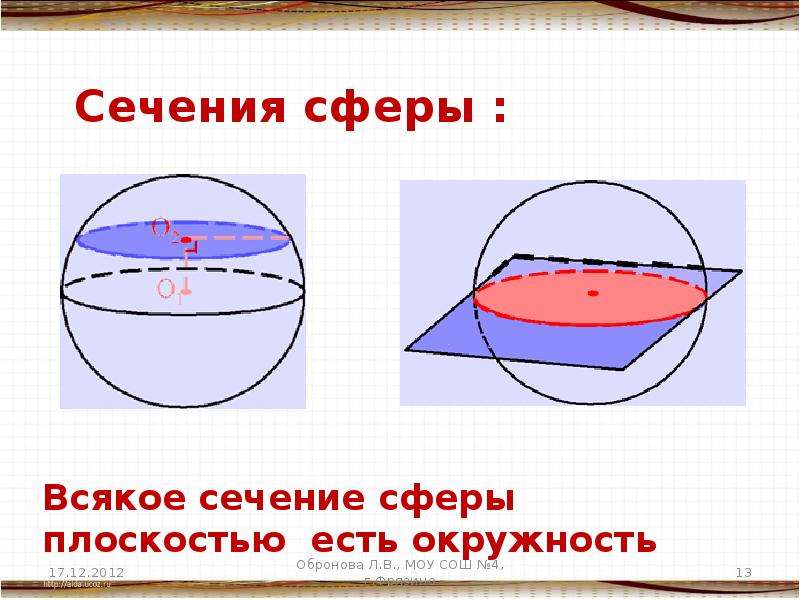
Рассмотрите осевое сечение с разных углов, чтобы увидеть, как меняются его формы в зависимости от положения сечения.

ПРОЕКЦИИ ТОЧЕК на поверхности шара (сферы). Построение трех проекций точек на заданной сфере

Понимание осевого сечения важно для работы с геометрическими фигурами в 3D-пространстве, особенно при моделировании и проектировании.

Объем шара. Практическая часть. 11 класс.

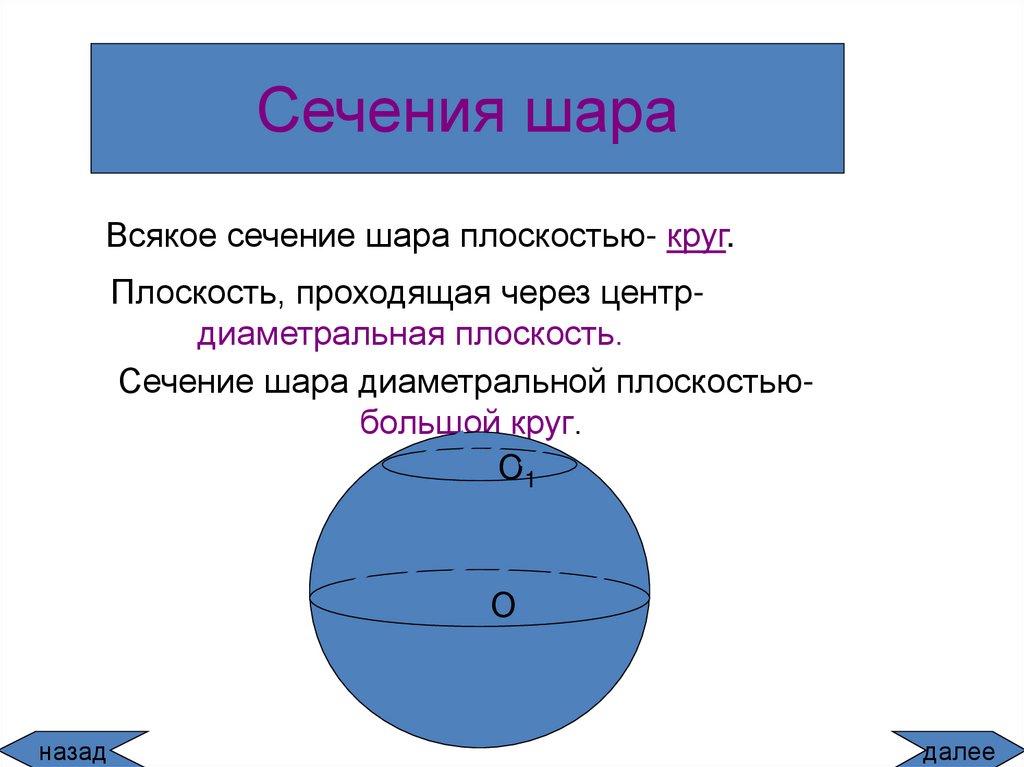
Используйте графические программы или 3D-моделирование для более глубокого понимания и визуализации осевых сечений.

Рисунок шара.
Не забывайте о значении плоскости сечения: изменение ее ориентации может существенно изменить форму сечения.

Сечение сферы
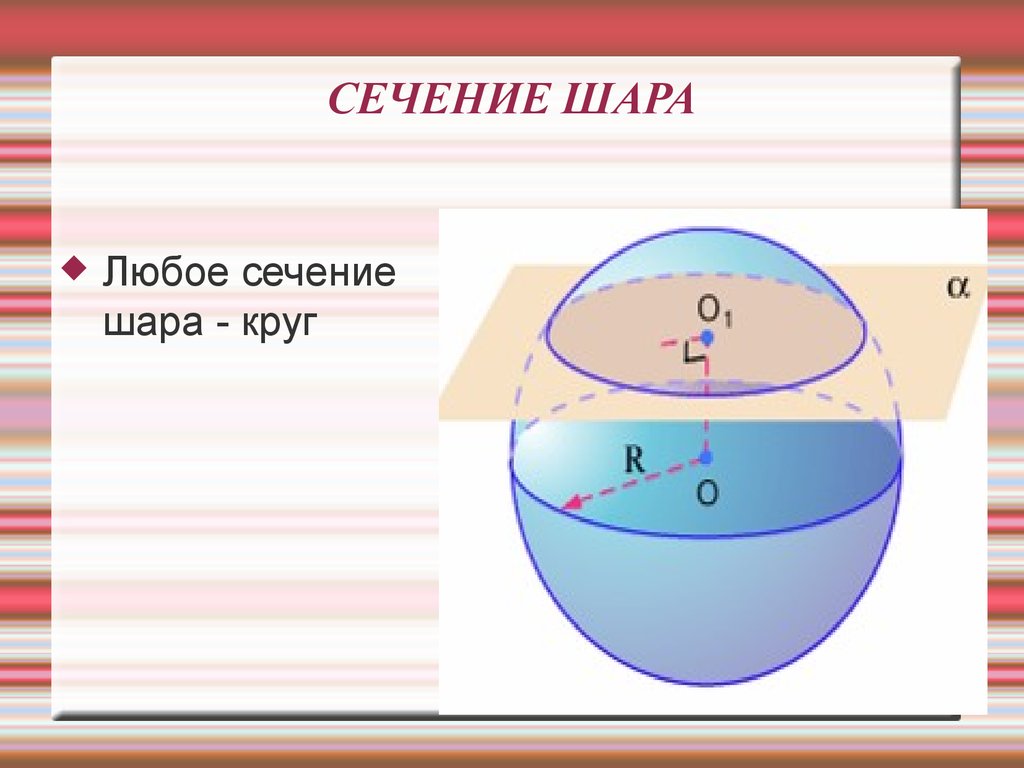
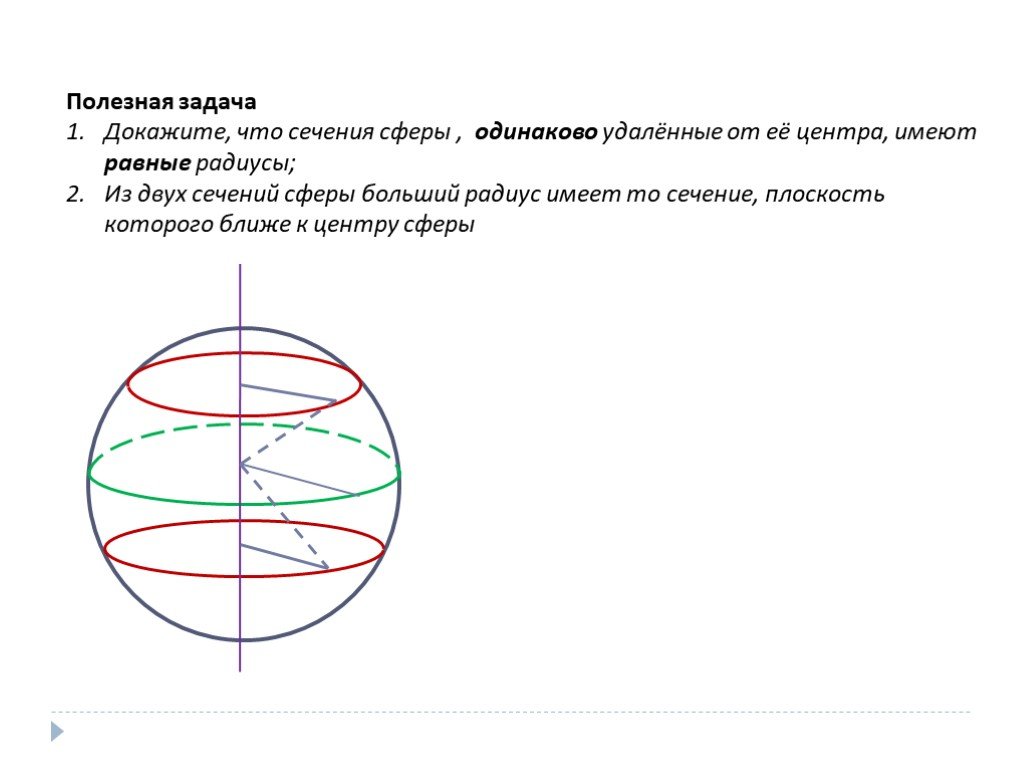
При работе с осевыми сечениями важно учитывать их пересечение с центром сферы или шара, что может повлиять на форму сечения.

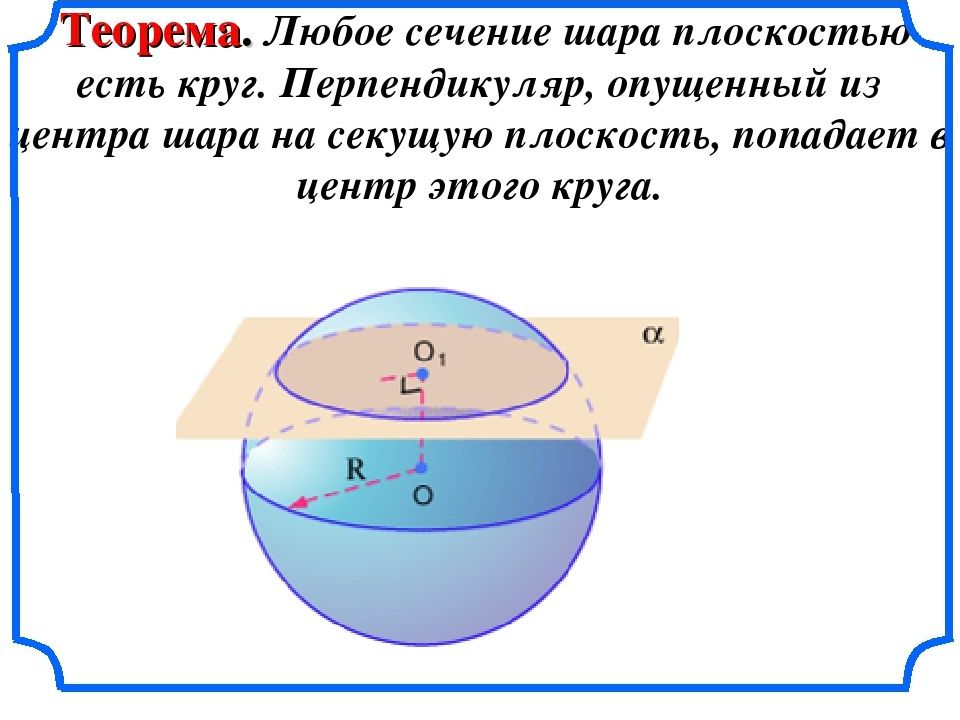
Знакомьтесь с примерами осевых сечений других геометрических фигур, чтобы лучше понять, как это работает в разных случаях.
Геометрия, 11 класс. Вписанные и описанные шары и сферы


При изучении осевого сечения полезно использовать физические модели или даже простые предметы, такие как мячики, для практических экспериментов.

Разгадка сочинского шара. Кто оставил сферы в лесу и для чего они?
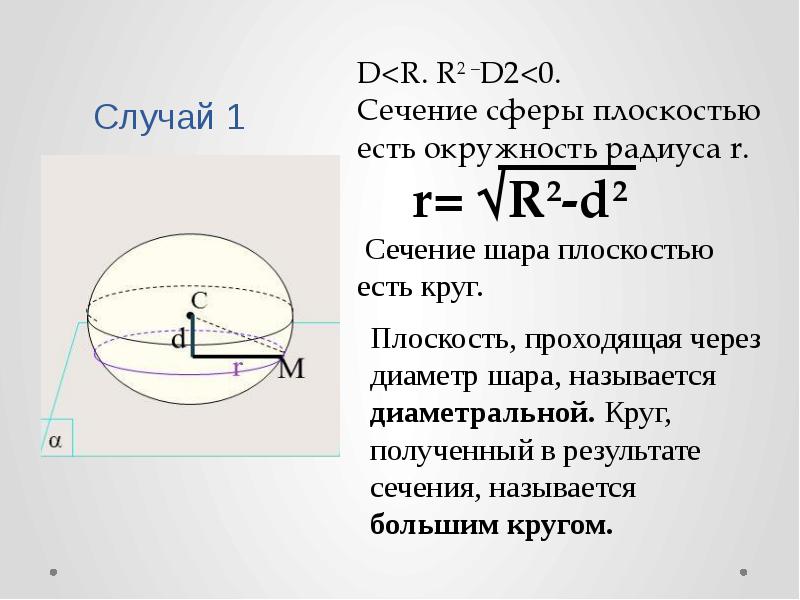
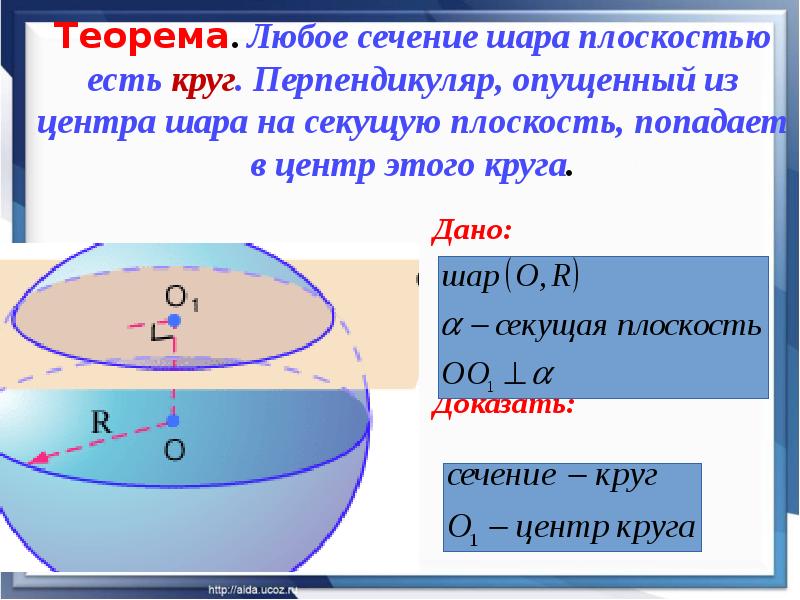
Запоминайте основные типы сечений, такие как круг, эллипс и другие, которые могут возникать в зависимости от угла сечения.
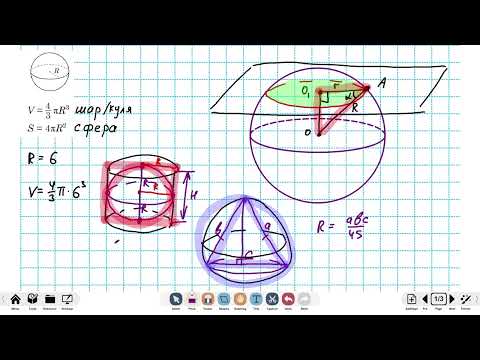
Сфера и шар. Сечение сферы. Вписанная и описанная сфера
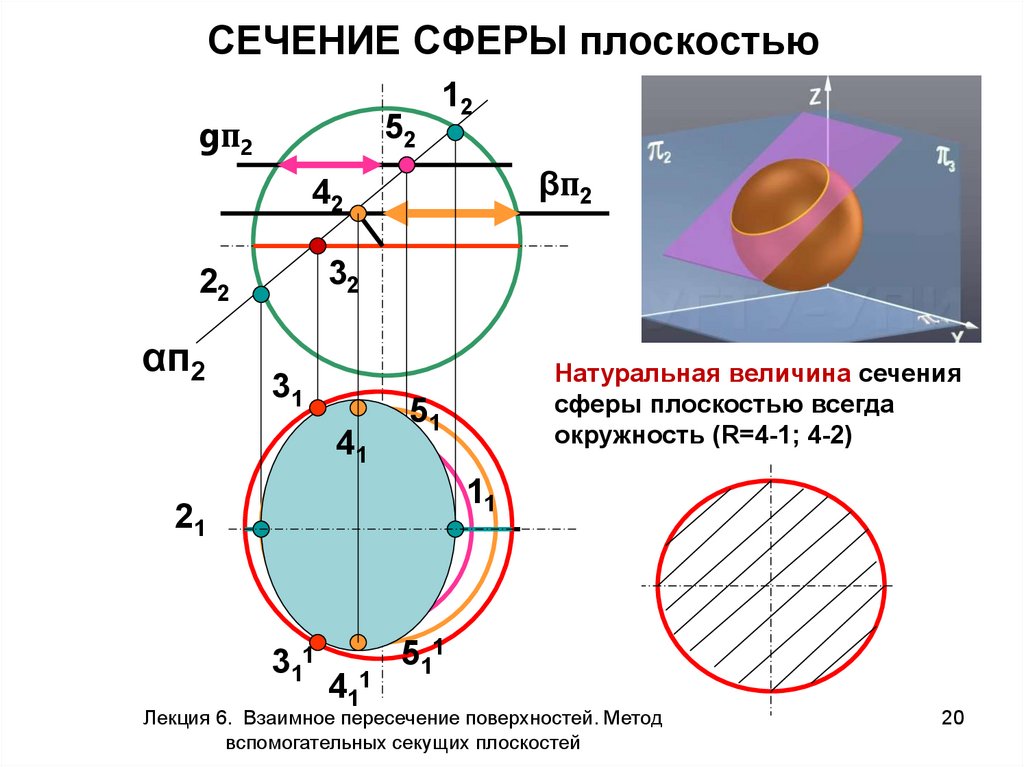
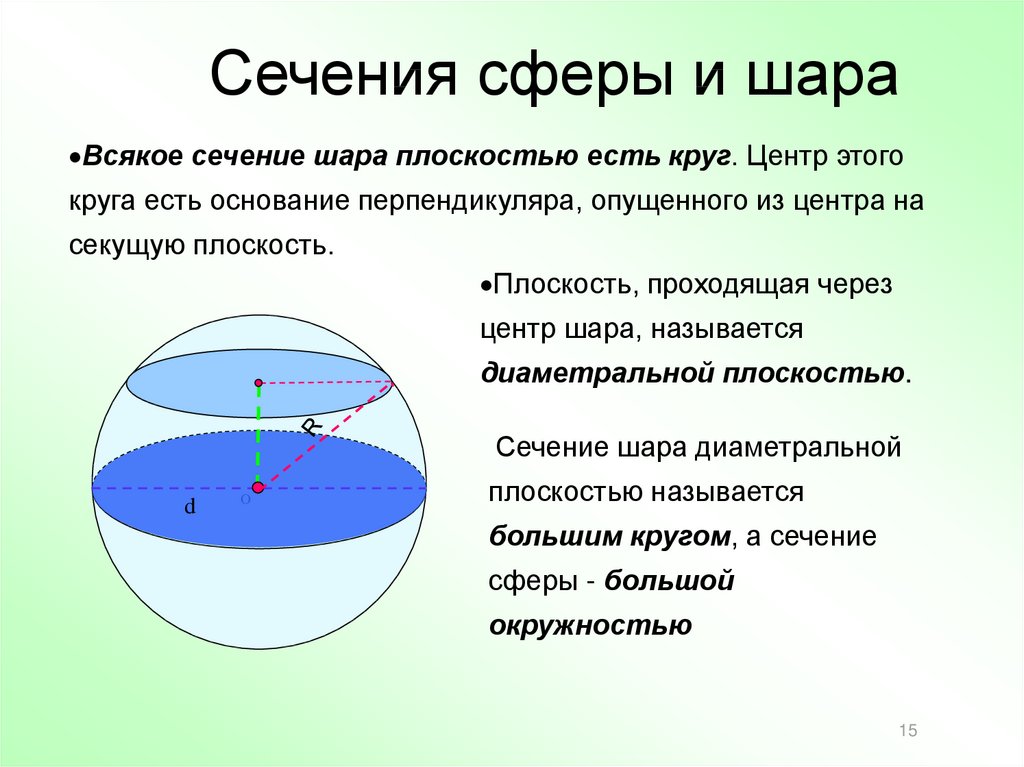
Не стесняйтесь задавать вопросы учителям или специалистам, если что-то непонятно: правильное понимание концепции поможет вам решать более сложные задачи.
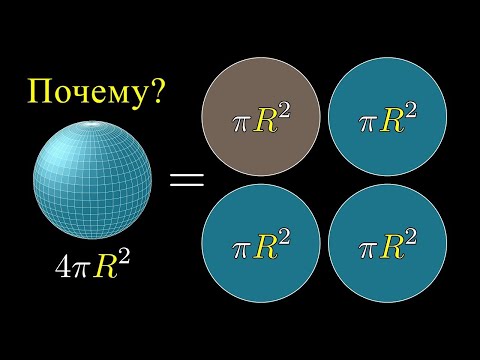
Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]
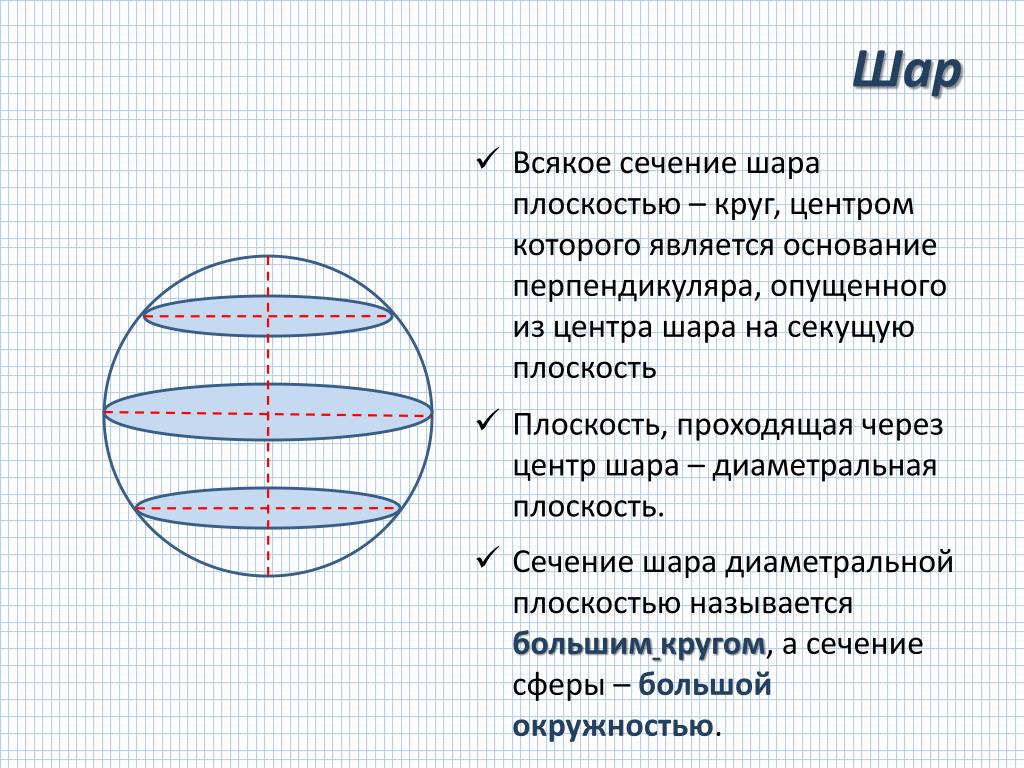

8. Классификация движений сферы