Окружность равностороннего треугольника: свойства и построение
Окружность, описанная вокруг равностороннего треугольника, представляет собой уникальную геометрическую фигуру, где все вершины треугольника лежат на одной окружности. Это связано с равенством сторон и углов, что делает процесс построения максимально простым и красивым.


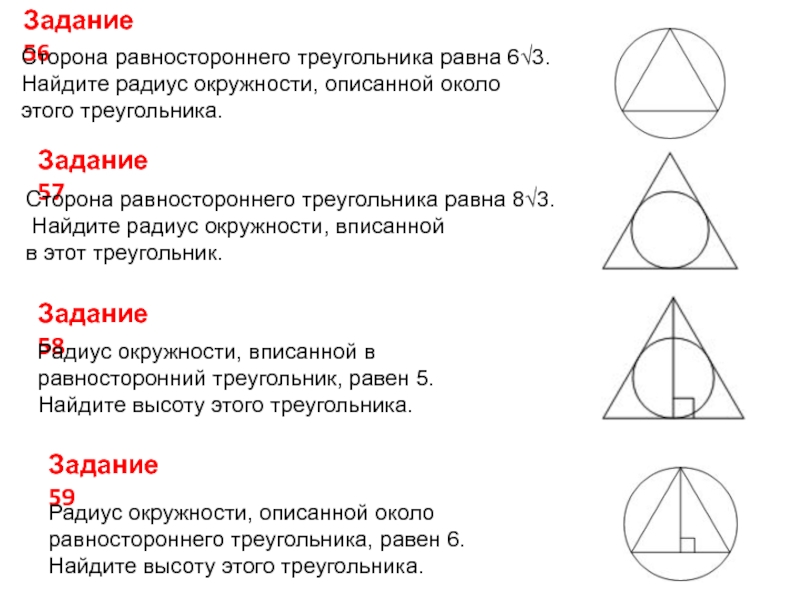
Начните с определения центра окружности: это точка пересечения медиан, биссектрис и высот треугольника.
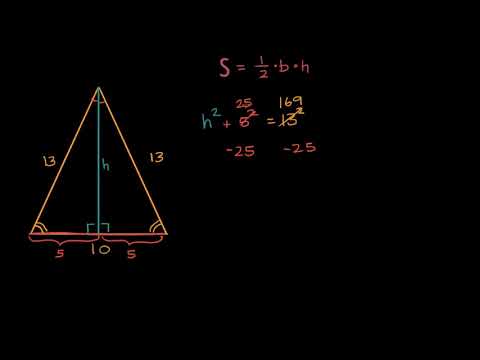
Нахождение площади равнобедренного треугольника при помощи теоремы Пифагора - Геометрия - Алгебра
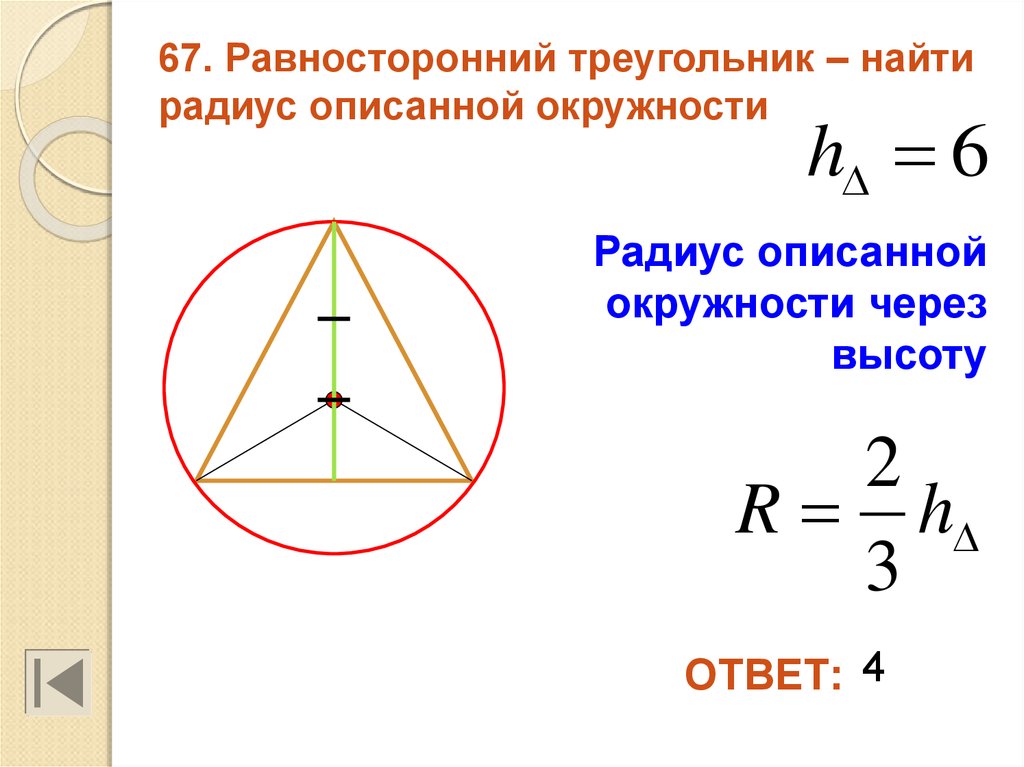
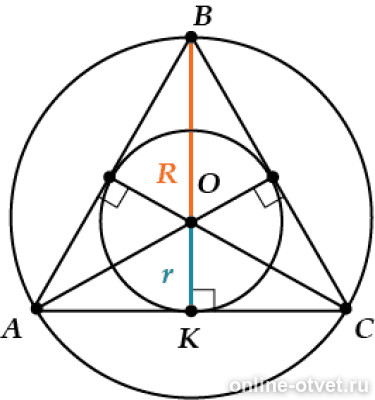
Для точного построения используйте циркуль: радиус равен расстоянию от центра до любой из вершин треугольника.

Вписанная и описанная окружности - Лайфхак для запоминания
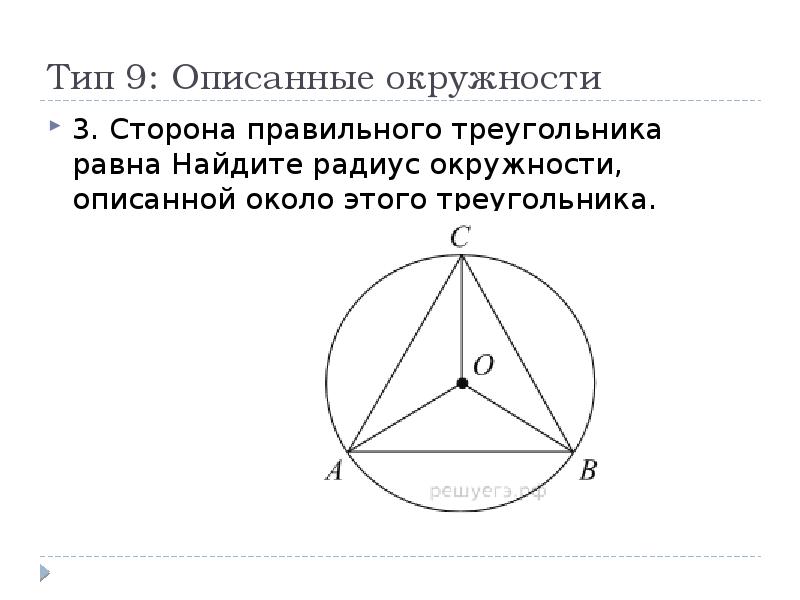
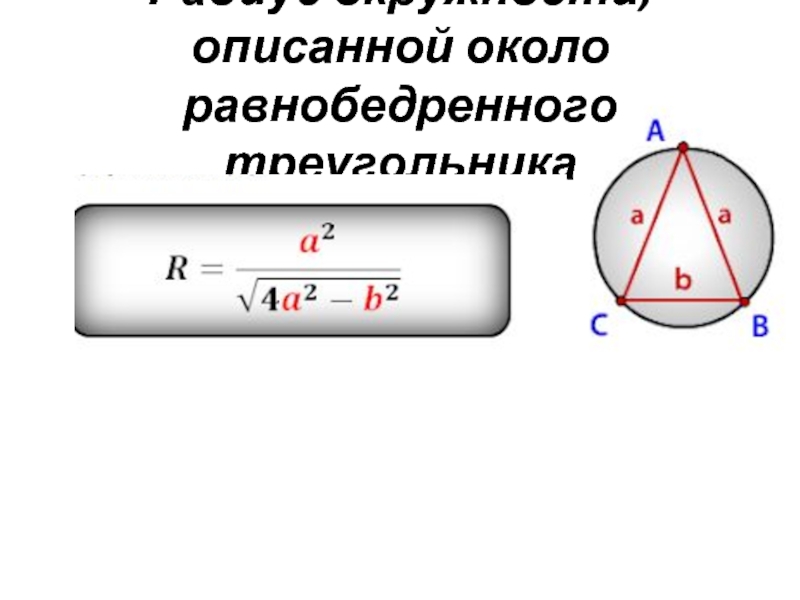
Если вы работаете в графических редакторах, активируйте инструмент для построения окружностей и задайте точку центра.

Окружность вписанная в треугольник и описанная около треугольника.
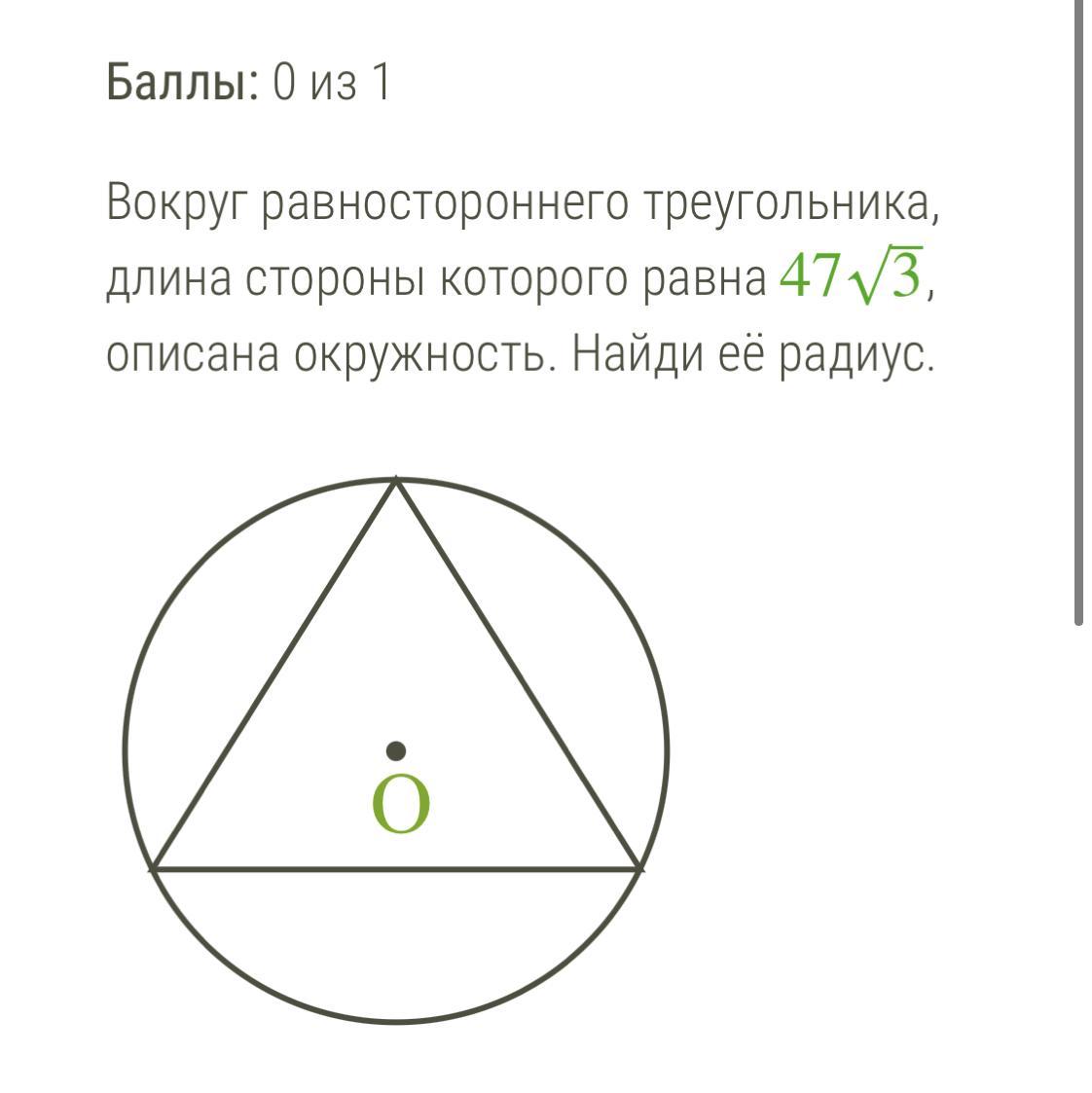

При практическом применении важно помнить, что равносторонний треугольник всегда симметричен относительно всех своих осей.

Построить описанную окружность (Задача 1)
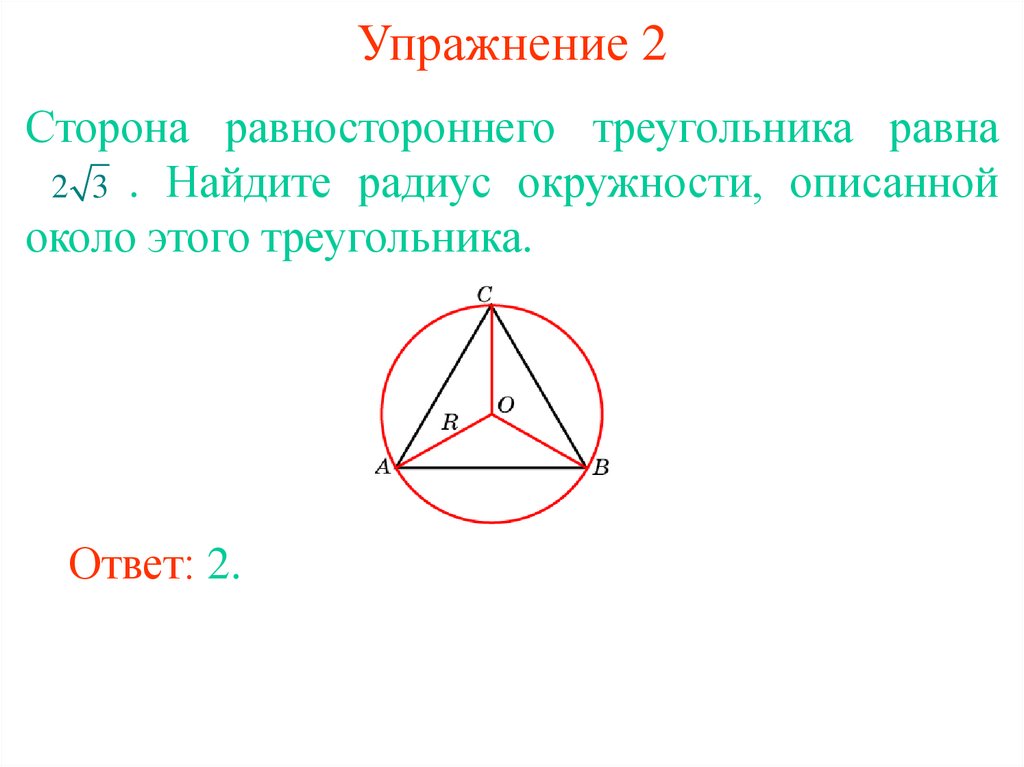
При ручном черчении используйте линейку и транспортир для точного измерения углов в 60 градусов.

Как Найти Радиус Сегмента на Потолке. Радиус Окружности По Хорде И Высоте Сегмента
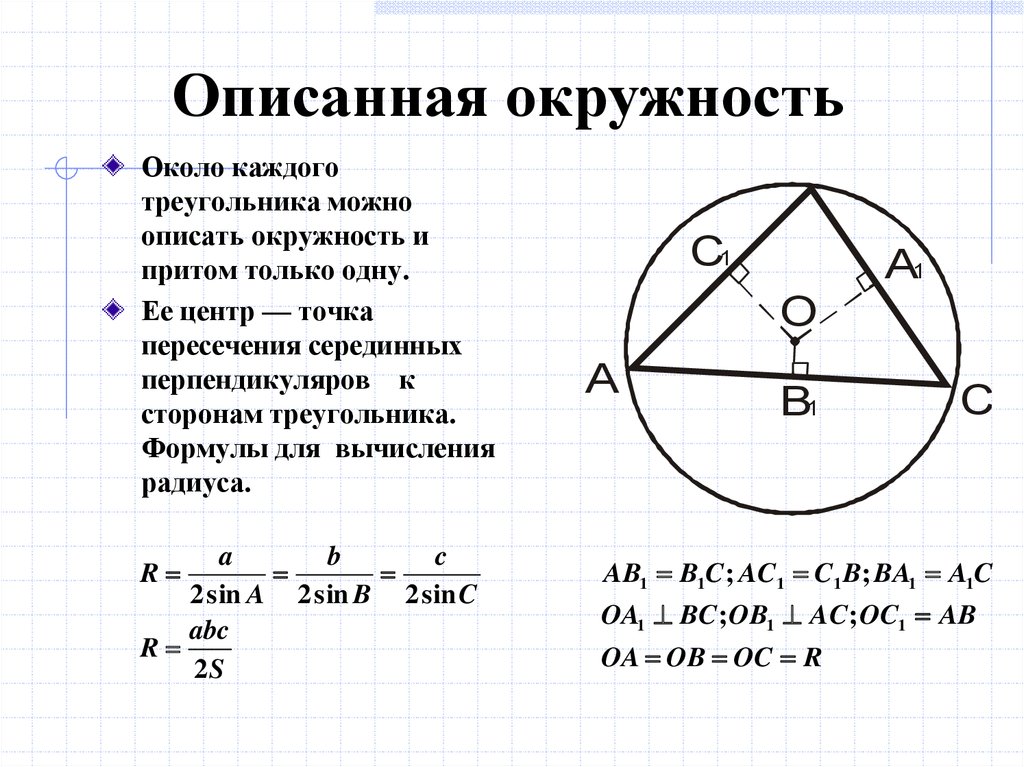

Запомните формулу радиуса: R = a / √3, где a — длина стороны треугольника.

Строим вписанную в данный треугольник окружность (Задача 2).
Для проверки точности постройки убедитесь, что расстояние от центра до всех вершин одинаковое.
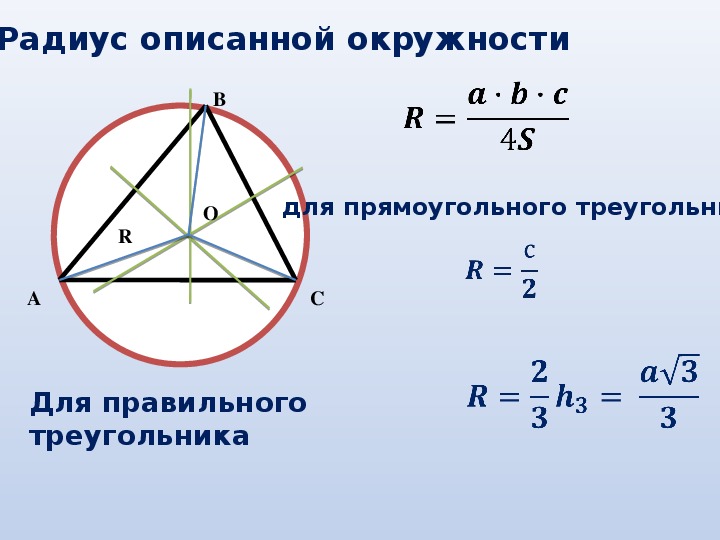
Если окружность строится на компьютере, используйте функции сетка и привязка для упрощения работы.
Тригонометрическая окружность. Как выучить?

2047 радиус окружности описанной около правильного треугольника равна 36 корней из 3
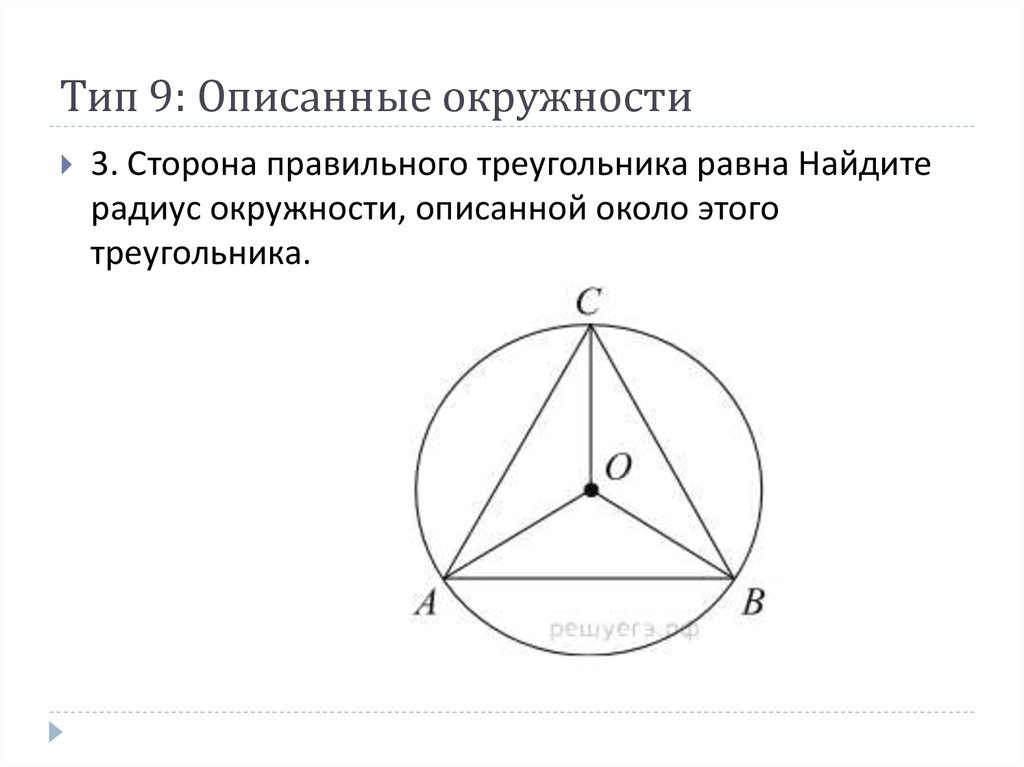

Знание свойств равностороннего треугольника облегчит работу: все его стороны и углы равны.

Помните, что описанная окружность — это лишь один из способов визуализации симметрии треугольника.
