Как изучить свойства описанной окружности четырехугольника: советы и фото
На этой странице вы найдете подробное описание свойств окружности, описанной вокруг четырехугольника, полезные советы и яркие фотографии, которые помогут вам разобраться в теме и применить знания на практике.


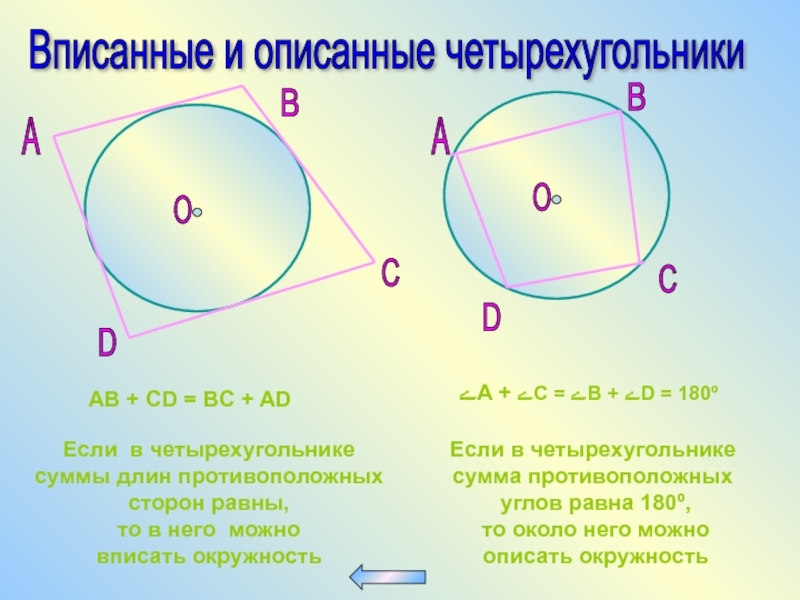
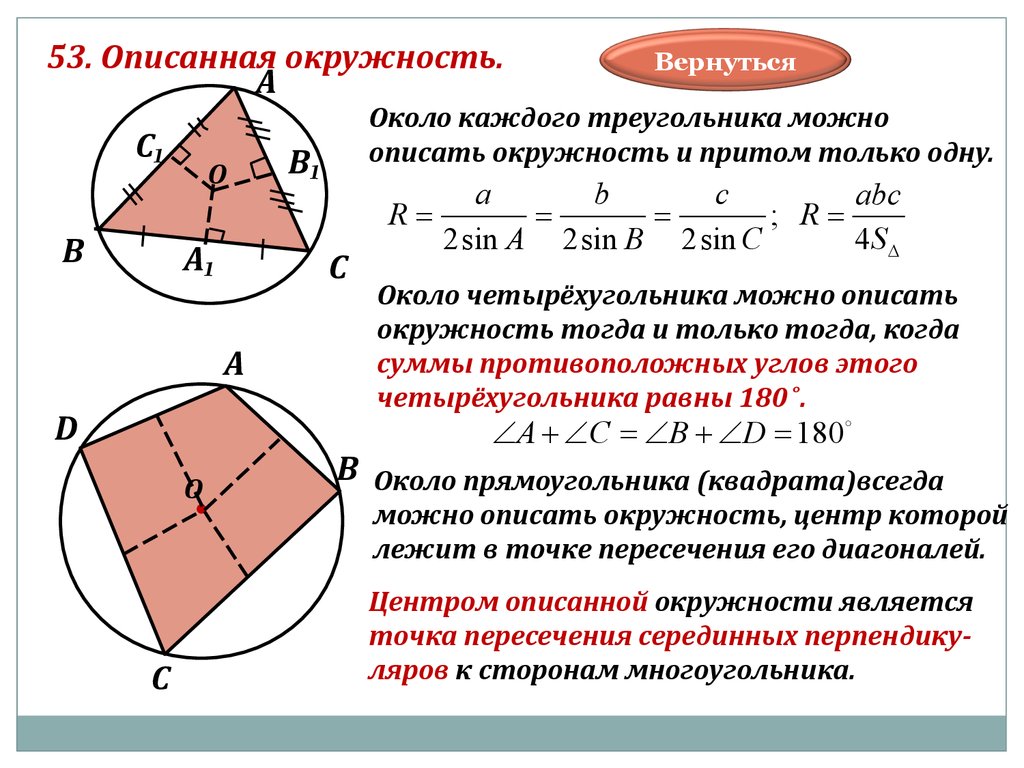
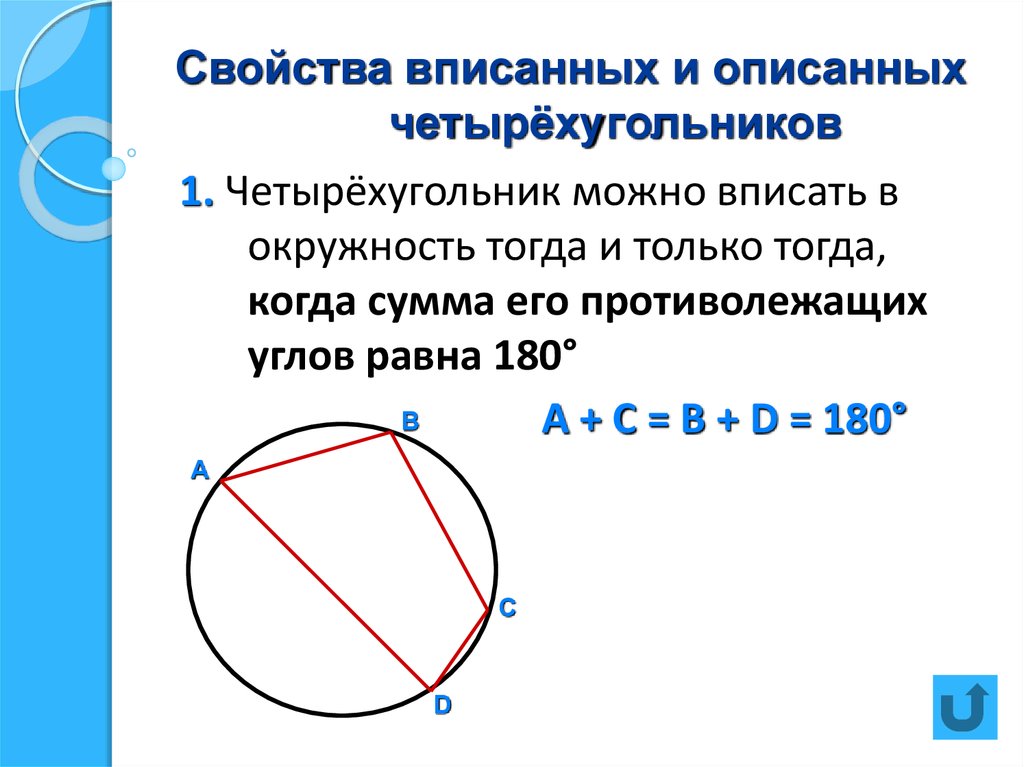
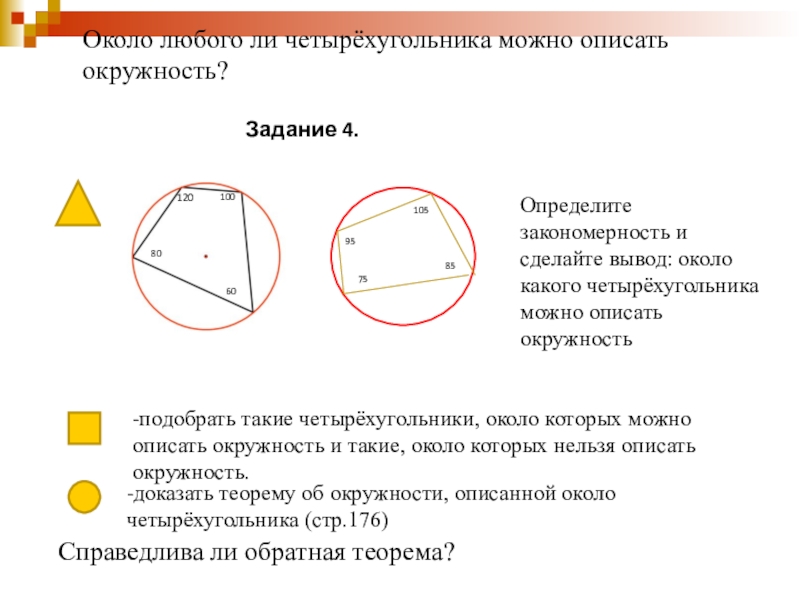
Всегда проверяйте, является ли четырехугольник вписанным: сумма его противоположных углов должна быть равна 180°.
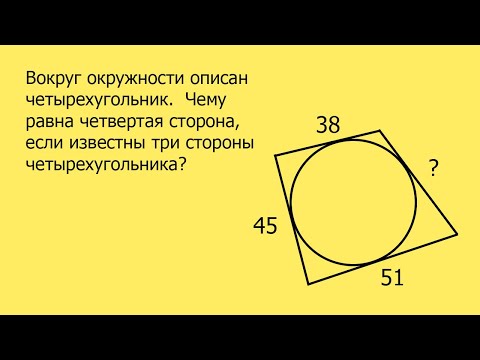
Уроки геометрии. Одно замечательное свойство четырехугольника, описанного вокруг окружности.
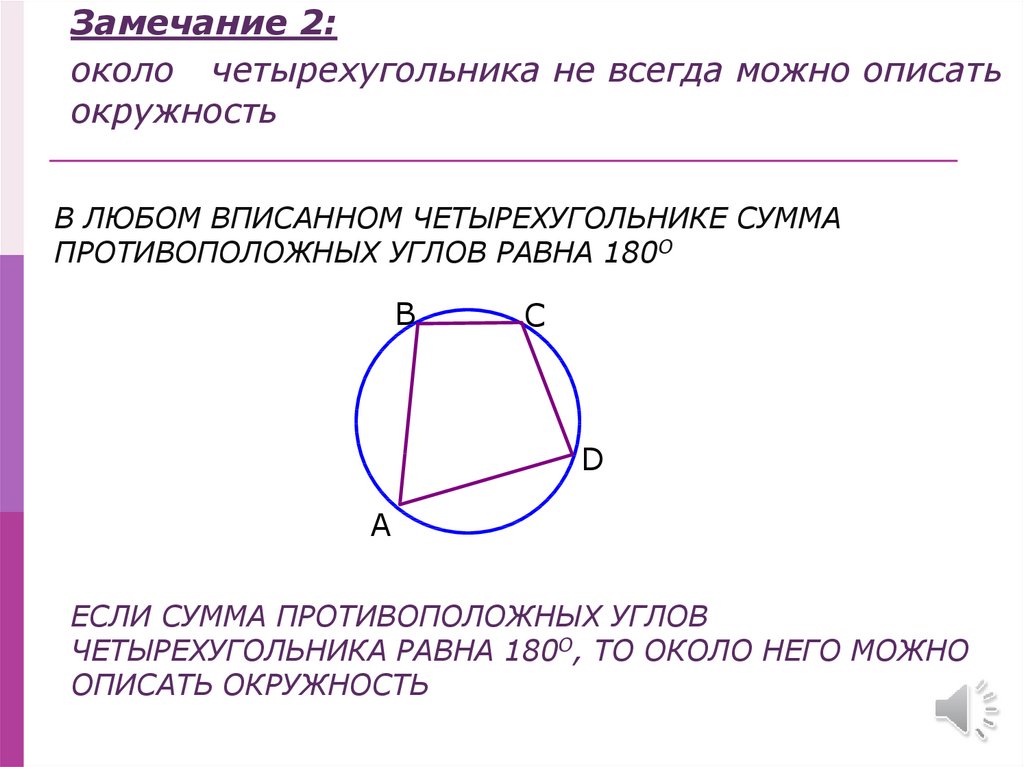

Для точного построения окружности используйте циркуль и определите центр как точку пересечения серединных перпендикуляров к сторонам четырехугольника.

Математика. Окружность: Описанный четырехугольник. Центр онлайн-обучения «Фоксфорд»

Используйте свойства вписанной окружности для решения задач по геометрии, например, для нахождения длины сторон или углов.

Окружность №16 из ОГЭ. Вписанные и описанные многоугольники. Квадрат и окружность.

Если четырехугольник не является вписанным, проверьте возможность его преобразования в такой путем изменения углов.

Вписанная и описанная окружности - Лайфхак для запоминания
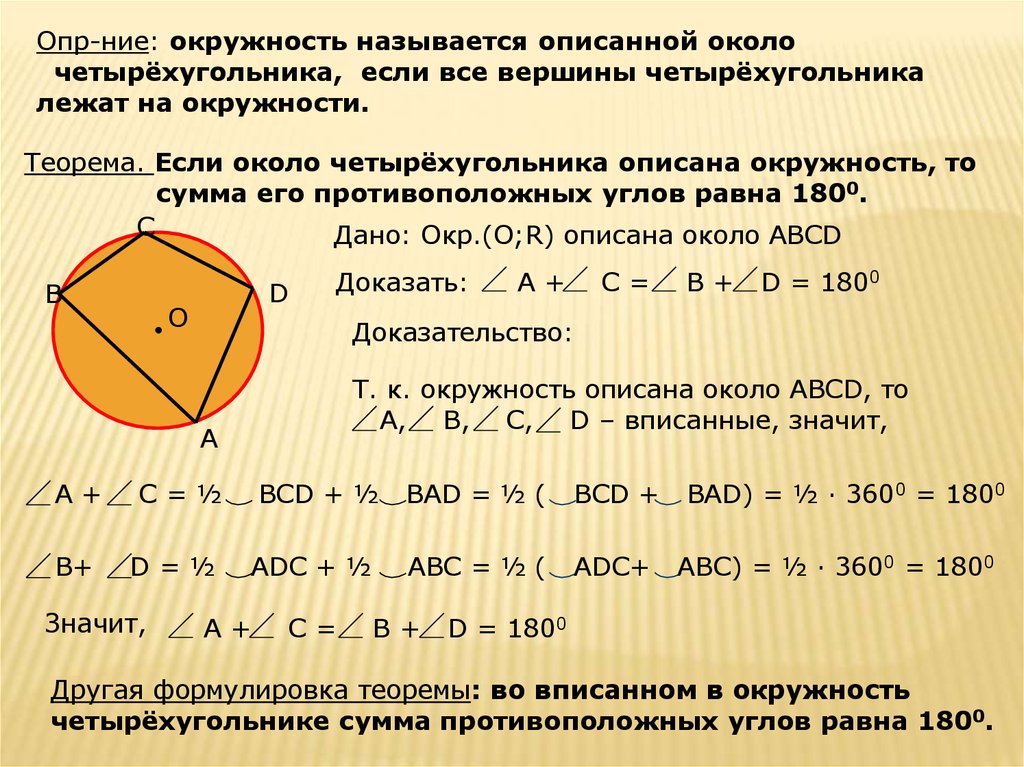
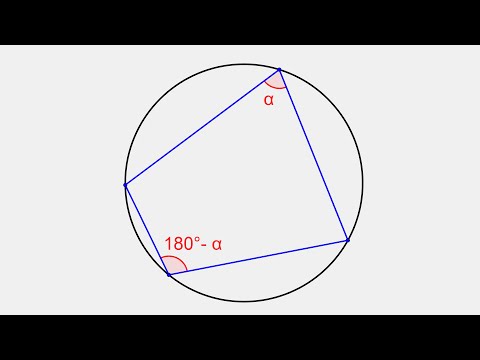
Используйте теорему Птолемея для проверки вписанности: произведение диагоналей должно быть равно сумме произведений противоположных сторон.
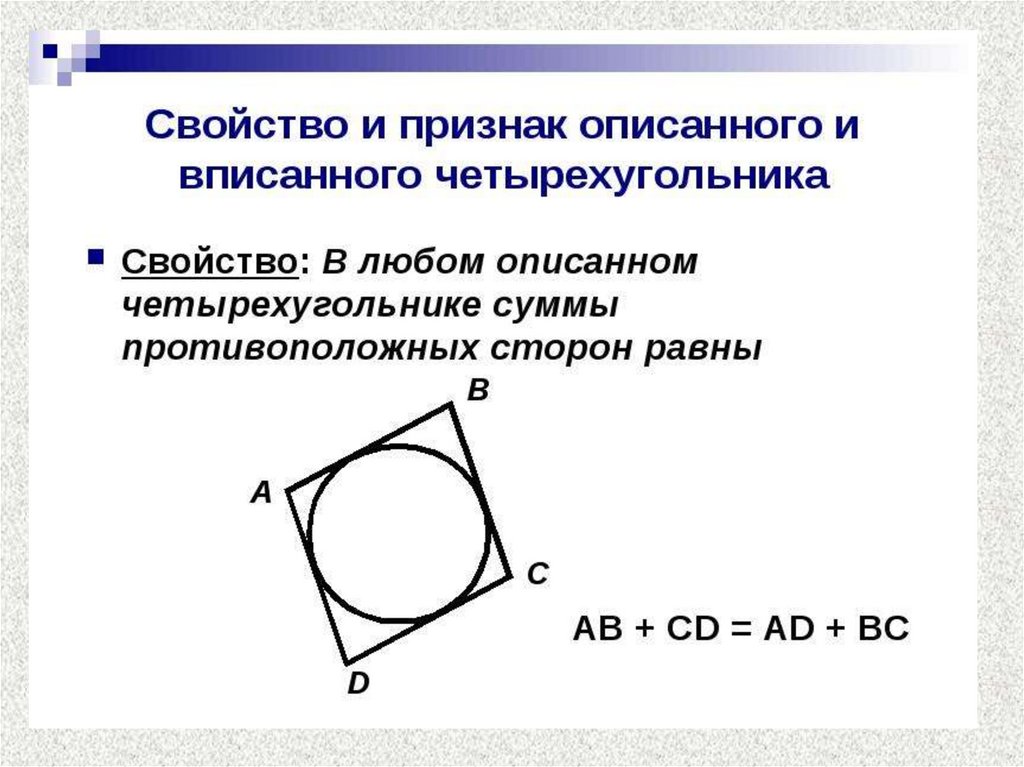
Свойство и признак вписанного четырехугольника
При построении окружности в геометрических задачах не забывайте учитывать масштаб и пропорции чертежа.


Для упрощения расчетов запишите известные длины сторон и углы в таблицу или блокнот.

Четырехугольники, вписанные в окружность. 9 класс.

Используйте математические программы или приложения для автоматизации построений и проверки решений.

Геометрия. Вписанная и описанная окружности.

Окружность, описанная вокруг четырёхугольника - Математика

Изучайте примеры реальных задач с использованием окружности, описанной вокруг четырехугольника, чтобы лучше понять теорию.

Вписанные и описанные четырехугольники. Практическая часть. 9 класс.

Не забывайте проверять полученные результаты на логичность и соответствие условию задачи.
Вписанная и описанная окружности. Задачи