Решение и анализ однородных дифференциальных уравнений: полезные советы
Однородные дифференциальные уравнения являются важной частью теории дифференциальных уравнений. В данной подборке собраны полезные советы и методы, которые помогут разобраться в особенностях их решения, а также предложены практические рекомендации для эффективного освоения материала.



При решении однородных линейных дифференциальных уравнений важно учитывать особенности их характеристического уравнения.

Дифференциальные уравнения для самых маленьких


Для нахождения общего решения однородного уравнения можно использовать метод разделения переменных или метод интегрирования по частям, в зависимости от его вида.

Сергеев И. Н. - Дифференциальные уравнения - Введение в дифференциальные уравнения
Важно помнить, что для однородных уравнений с постоянными коэффициентами характеристическое уравнение всегда будет иметь корни, которые определяют вид решения.
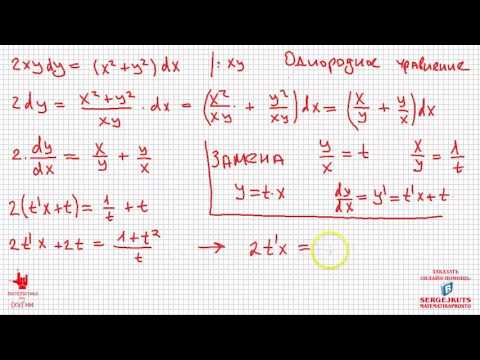
18+ Математика без Ху%!ни. Дифференциальные уравнения. Однородное уравнение.


Если однородное уравнение имеет повторяющиеся корни характеристического уравнения, решение будет включать экспоненциальные функции, умноженные на полиномы.

4. Однородные дифференциальные уравнения (часть 1)
Для нелинейных однородных уравнений может потребоваться применение численных методов, таких как метод Эйлера или Рунге-Кутты.
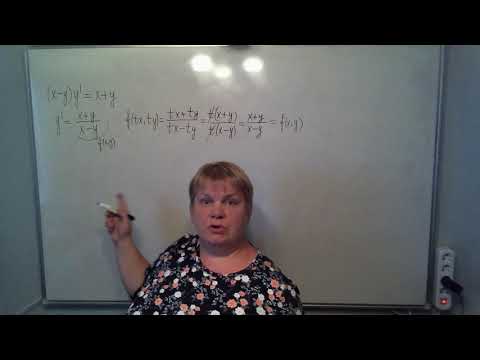
Однородные дифференциальные уравнения первого порядка

Понимание геометрической интерпретации решения однородного уравнения помогает лучше осознавать его физический смысл и поведение системы.

Дифференциальные уравнения, 3 урок, Однородные уравнения


В случае сложных уравнений с переменными коэффициентами полезно применять метод преобразования Лапласа для упрощения вычислений.

Для улучшения понимания решений однородных уравнений рекомендуется решать задачи с различными начальными условиями, чтобы наблюдать за изменениями решений.

Однородное дифференциальное уравнение

#Дифуры II. Урок 2. Линейные однородные диф. уравнения n-го порядка с постоянными коэффициентами

При решении задач с однородными уравнениями важно тщательно проверять начальные и граничные условия, так как они могут существенно повлиять на решение.


Использование аналитических методов для простых уравнений и численных для более сложных поможет более эффективно освоить материал и практику в решении дифференциальных уравнений.

Размышляю над Хаосом и Равновесием - Диффуры


17. Полный дифференциал сложной функции. Инвариантность формы первого дифференциала