Объем конуса через интеграл: пошаговое руководство и полезные советы
На этой странице вы найдете полезные рекомендации по вычислению объема конуса с использованием методов интегралов, а также подробные примеры и объяснения шаг за шагом, которые помогут лучше понять этот процесс и успешно применить его на практике.



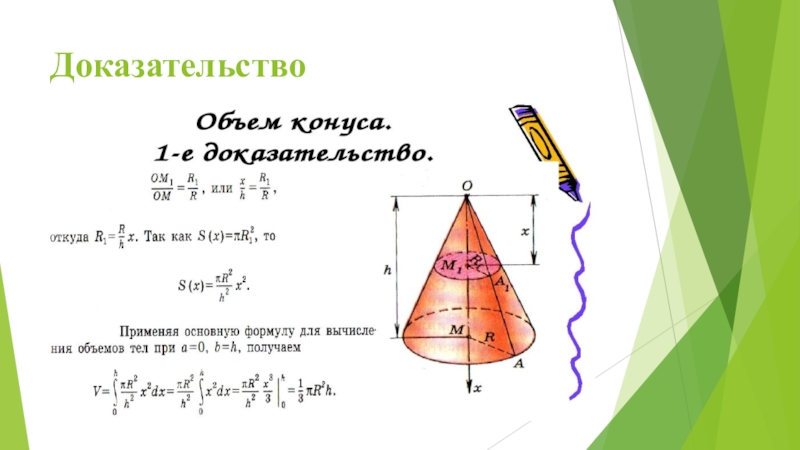
Для вычисления объема конуса через интеграл используйте формулу V = ∫π(y(x))^2 dx, где y(x) — радиус основания, зависящий от высоты.

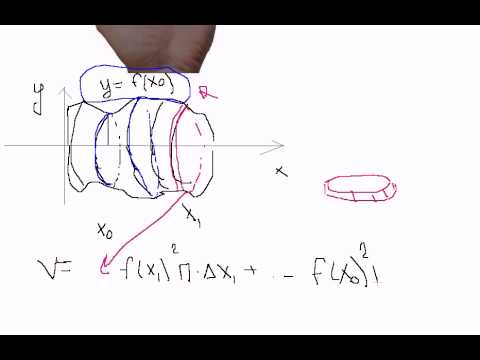
Volume of a Cone [1st Method: Summation Formula]

Проверьте границы интегрирования, они зависят от координат основания и вершины конуса, чтобы правильно определить объем.

Вычисление объемов с помощью определенного интеграла
Чтобы избежать ошибок при вычислении, всегда перепроверяйте работу функции радиуса, особенно если конус имеет сложную форму.

Урок геометрии 11 класс: объем конуса

Не забывайте учитывать симметрию фигуры, поскольку конус является симметричным относительно своей оси, что упрощает задачу.
Объём тела likerkacinema.ruрный интеграл
При решении задачи используйте подходящие методы подстановки и трансформации, чтобы упростить интеграл.

11 класс, 33 урок, Вычисление объемов тел с помощью определённого интеграла
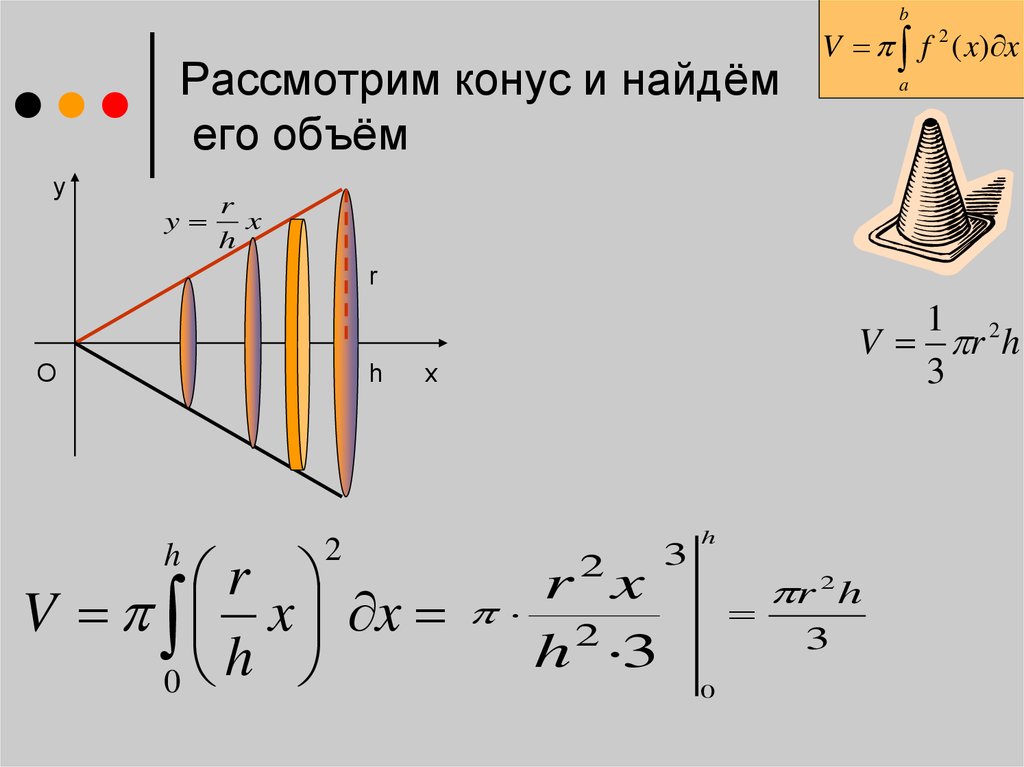

Если конус описан функцией, не забудьте выразить радиус как функцию от высоты, а затем подставить в интеграл.

Для большей точности в расчетах используйте численные методы интегрирования, если аналитическое решение слишком сложное.
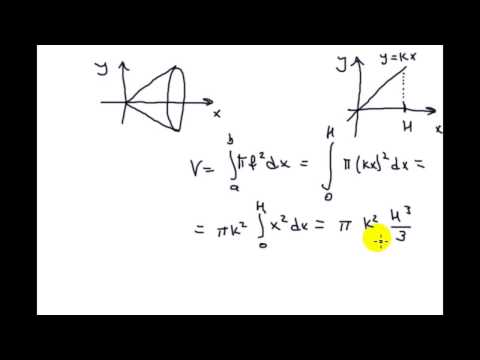
Интегралы - задачи, приводящие к понятию интеграла - объём тела вращения - конкретные примеры - 2

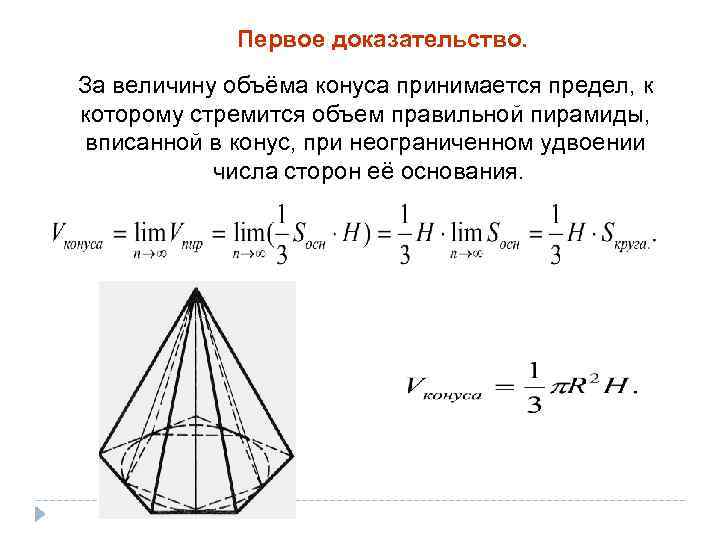
Если у вас есть возможность, решите задачу в несколько этапов, начиная с простых примеров для закрепления материала.
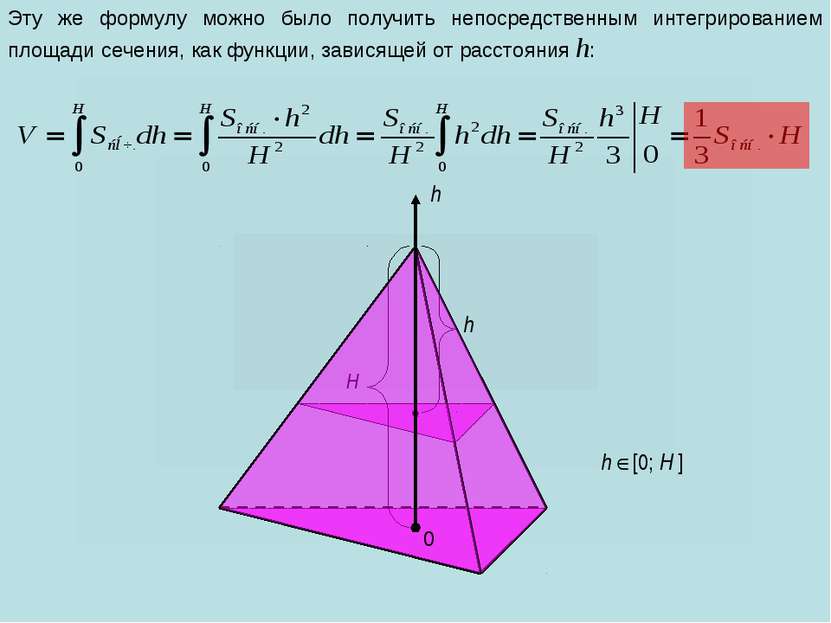
Для более глубокого понимания попробуйте изучить задачу с разных точек зрения, включая использование координат и вычисление через площадь сечений.

11 класс, 36 урок, Объем конуса

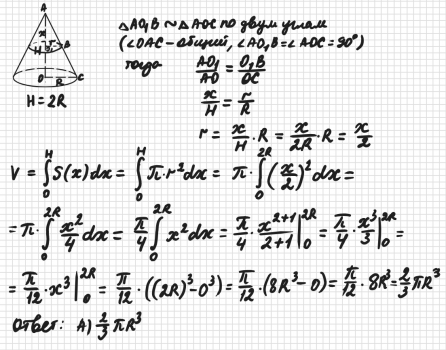
Важным шагом является правильная постановка задачи: правильно определите параметры конуса и соответствующие переменные для интеграла.