Основные методы и советы для нахождения объема тел вращения вокруг оси
Этот раздел посвящен тому, как вычислить объем различных фигур вращения вокруг оси, а также полезным рекомендациям для правильного применения математических методов на практике. Рассмотрим теоретические и практические аспекты данной задачи, которые могут помочь вам лучше понять и решить подобные задачи.


Перед началом расчетов всегда проверяйте правильность выбранной оси вращения, чтобы избежать ошибок в вычислениях.

ПОИ6.С1. Пример (3-й) на объём тела вращения (вокруг ОХ) и задания для самостоятельной работы

Используйте метод интегрирования по цилиндрическим слоям для более точных вычислений объема сложных фигур вращения.
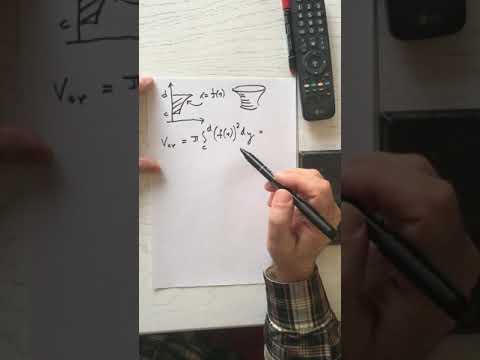
ПОИ5. Объём тела вращения (вокруг оси ОY).
Помните, что для простых тел вращения, например, цилиндров или конусов, существуют готовые формулы для объема, что ускоряет решение задач.

Видеоурок \

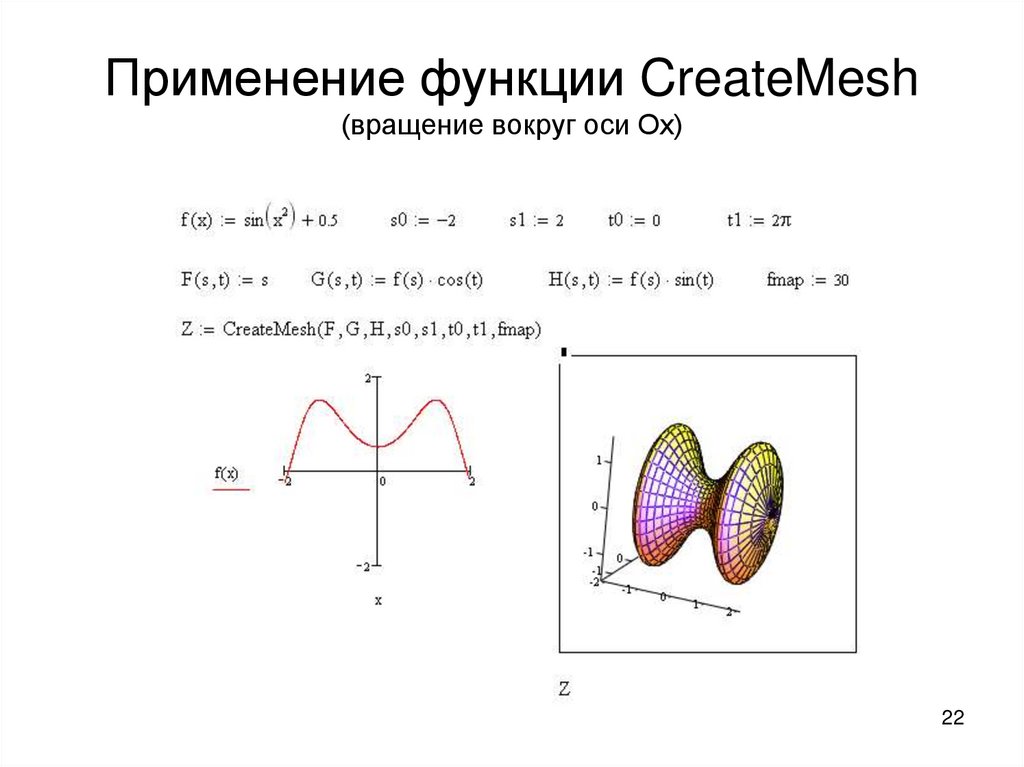
Не забывайте про единицы измерения. Все параметры (например, радиус или высоту) должны быть в одинаковых единицах, чтобы результат был корректным.

Интегралы №13 Объем тела вращения


Для сложных фигур вращения разбивайте их на несколько частей и вычисляйте объем каждой отдельно, а затем суммируйте полученные значения.

Объём тела вращения.

Понимание геометрии фигуры, которую вы вращаете, поможет правильно настроить границы интегрирования для вычисления объема.
Используйте графическое представление задачи, чтобы лучше визуализировать форму тела вращения и определить, какие параметры необходимо учитывать при расчете.
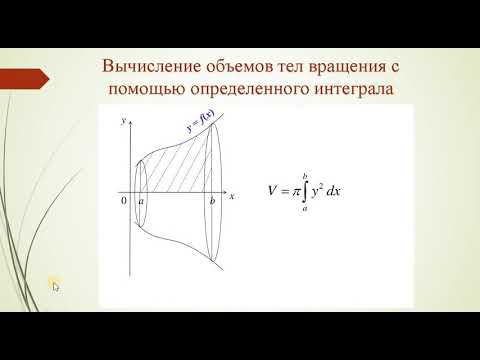
Вычисление объемов тел вращения (применение определенного интеграла)

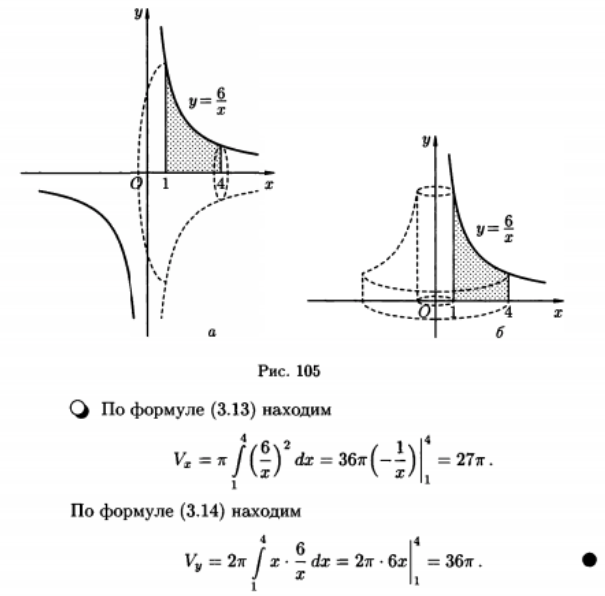
Для нахождения объема тел вращения вокруг произвольной оси используйте метод дисков или кольцевых сечений, в зависимости от формы задачи.

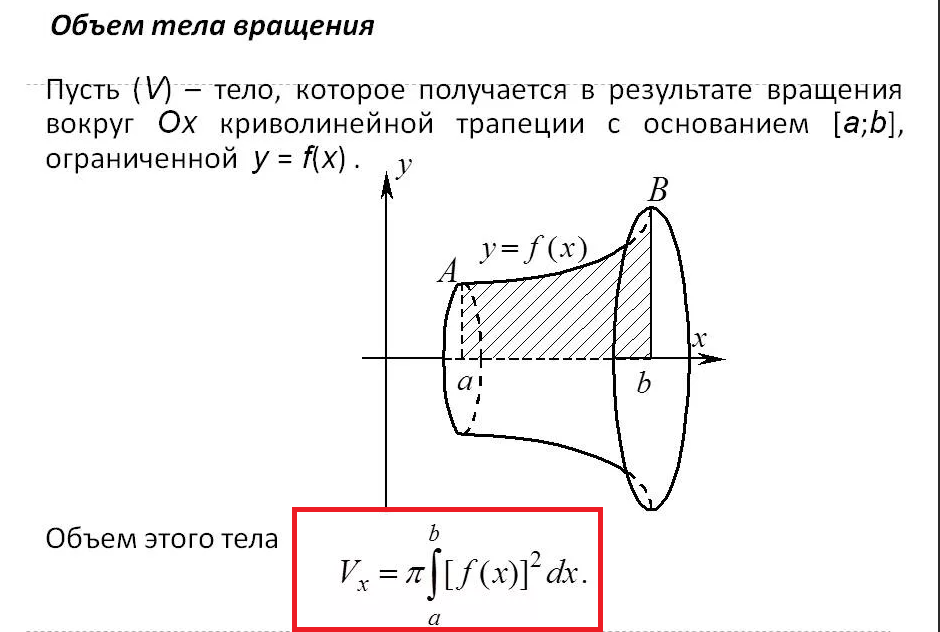
ПОИ4. Объём тела вращения (вокруг оси ОХ).
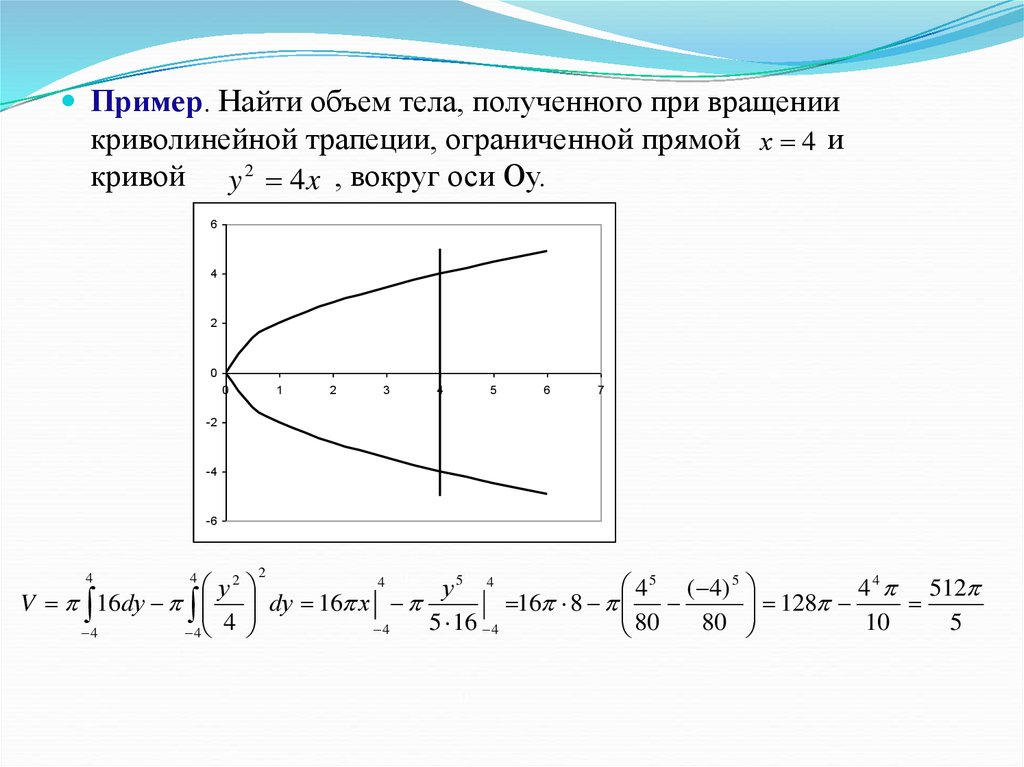
На практике, при использовании интегралов, часто удобнее сначала выразить функции в терминах полярных координат для упрощения расчетов.
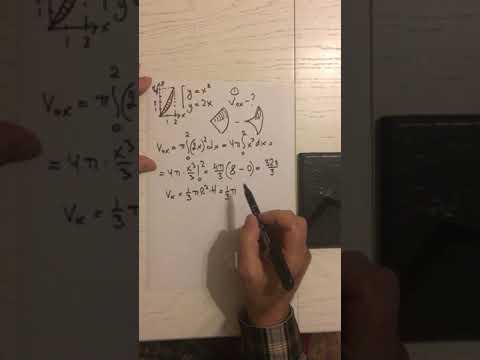
ПОИ6. Решение задачи об объёме тела вращения.
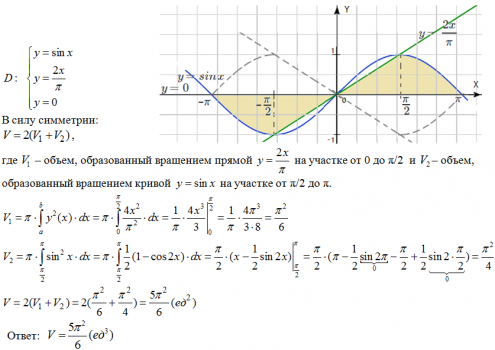
Не забывайте, что для тела вращения важна не только форма, но и плотность материала, если требуется учитывать массу, а не просто объем.

Объем тела вращения


Самый короткий тест на интеллект Задача Массачусетского профессора