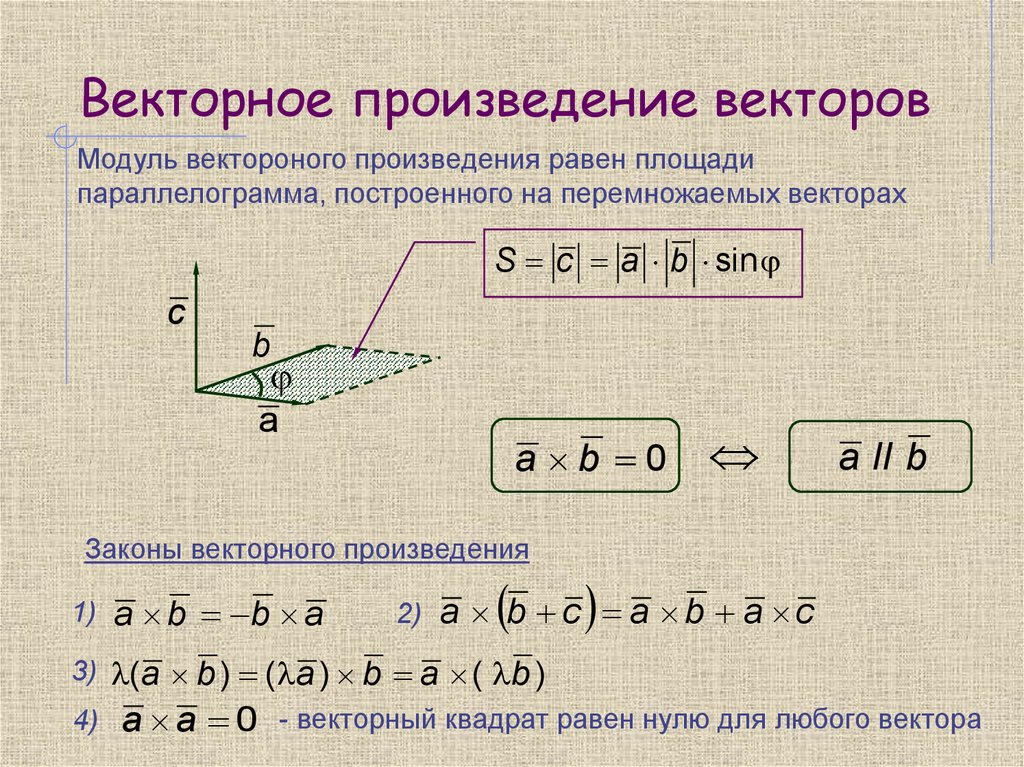
Как правильно вычислять косое произведение векторов на плоскости: основные принципы и советы
Косое произведение векторов на плоскости — это важная операция в геометрии и физике, которая помогает определить ориентацию векторов и площадь параллелограмма, образованного двумя векторами. На этой странице собраны полезные советы по вычислению косого произведения и его применению в различных задачах.
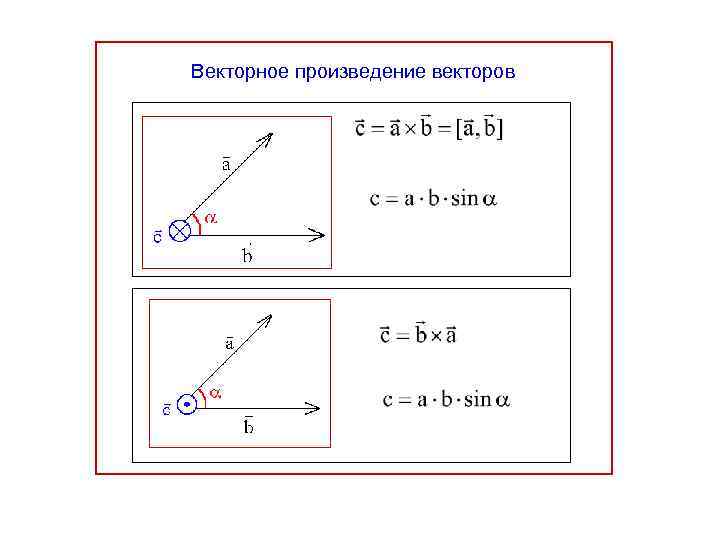
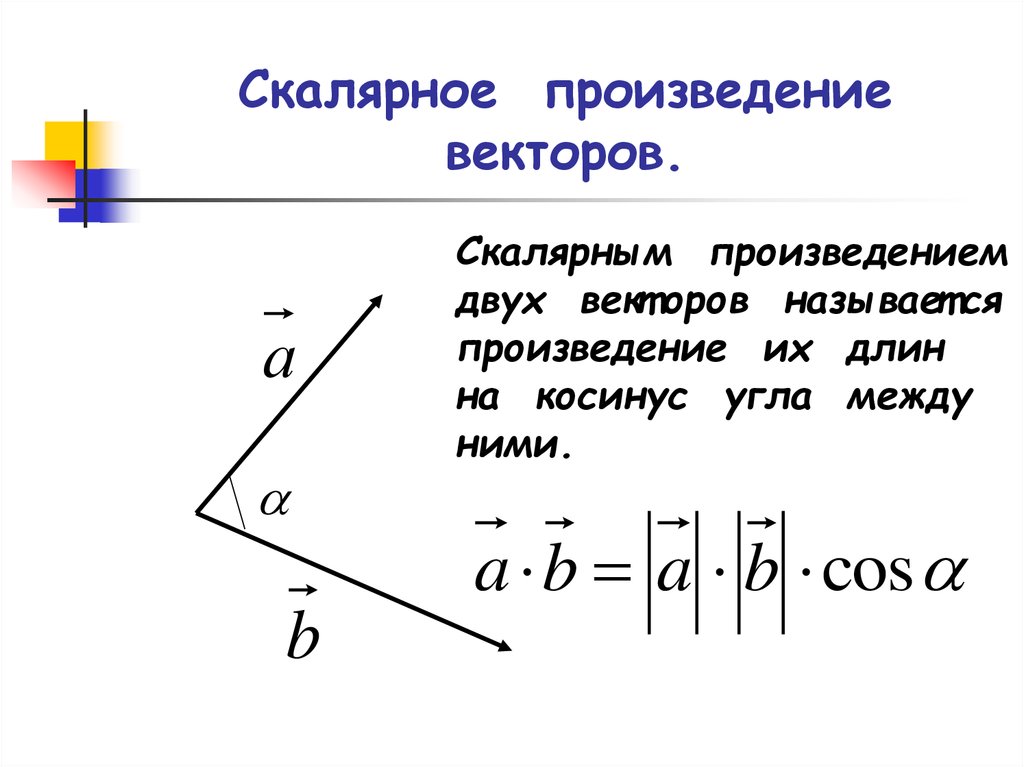
Для вычисления косого произведения двух векторов на плоскости используйте формулу: A × B = |A| * |B| * sin(θ), где θ — угол между векторами.

Вычислительная геометрия: Векторное произведение векторов. Центр онлайн-обучения «Фоксфорд»

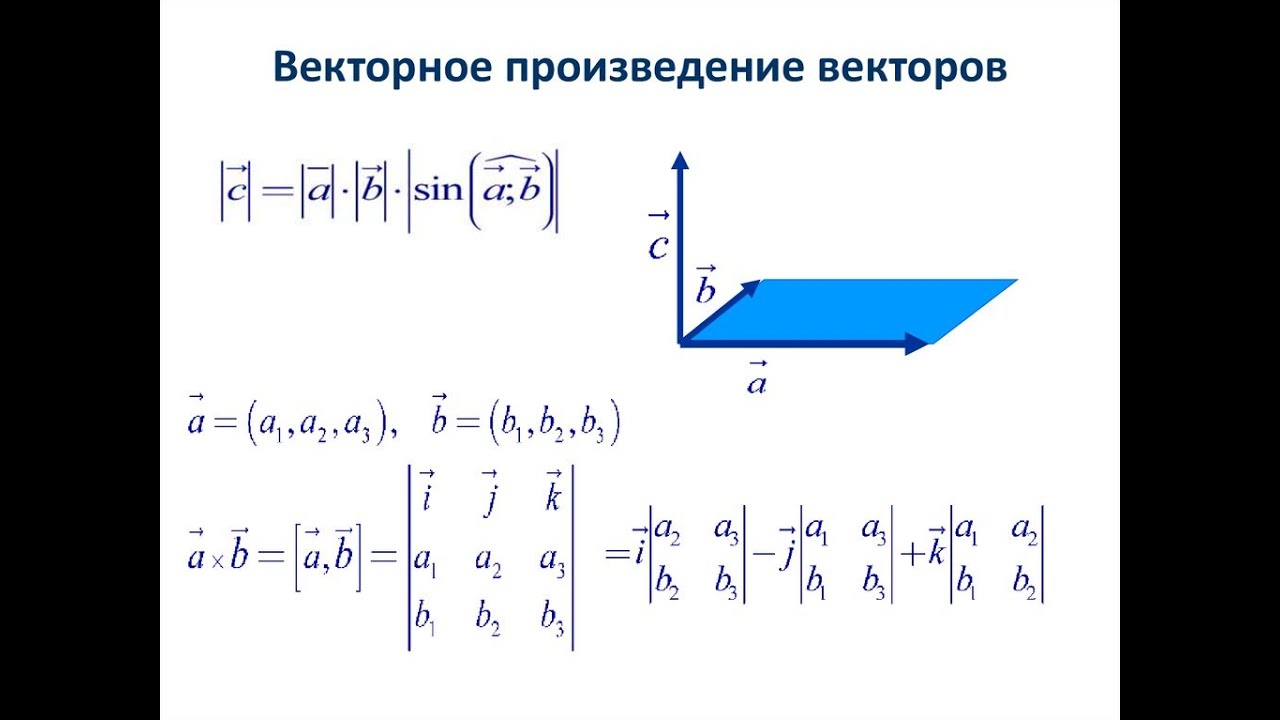
При работе с координатами векторов (x1, y1) и (x2, y2) косое произведение можно вычислить по формуле: A × B = x1 * y2 - x2 * y1.

Векторы на плоскости
Если косое произведение двух векторов равно нулю, это означает, что векторы коллинеарны (лежат на одной прямой).

Пенской А. В. - Аналитическая геометрия. Семинары - Скалярное произведение векторов

Косое произведение может использоваться для нахождения площади параллелограмма, образованного двумя векторами: S = |A × B|.

Векторы на плоскости

Это произведение важно для определения направления нормали к плоскости, если векторы представляют стороны параллелограмма.

Векторы на плоскости

Для векторов в трехмерном пространстве аналогичную операцию называют векторным произведением, но на плоскости применяется лишь двумерная версия.
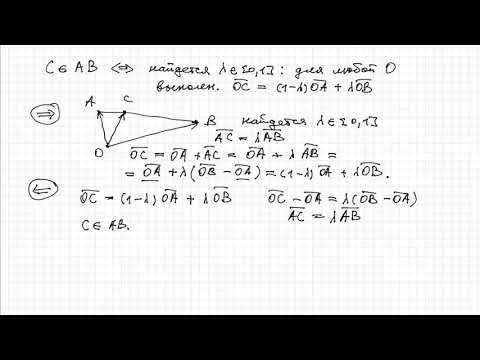
Векторы на плоскости.


При вычислении косого произведения векторов всегда обращайте внимание на знак результата, который зависит от ориентации векторов (по часовой стрелке или против).

Математика без Ху%!ни. Смешанное произведение векторов

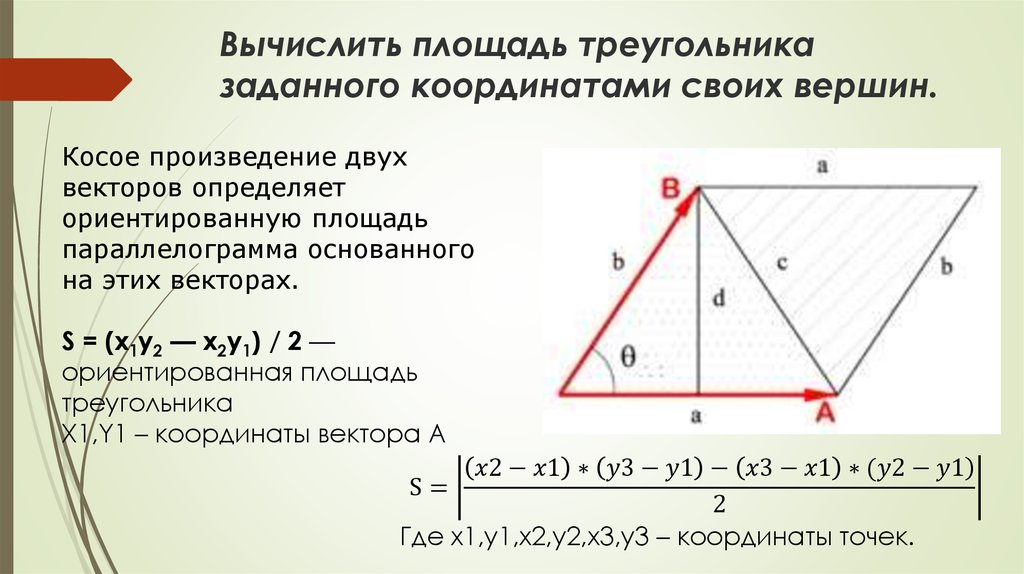
Если один из векторов является нулевым, косое произведение всегда будет равно нулю, независимо от второго вектора.


При решении задач на плоскости, где необходимо найти угол между двумя векторами, используйте косое произведение в сочетании с скалярным произведением.

Для упрощения вычислений часто используют правила направления и ориентации векторов, чтобы избежать ошибок в определении знака косого произведения.