Основные характеристики конуса как ограниченной геометрической формы
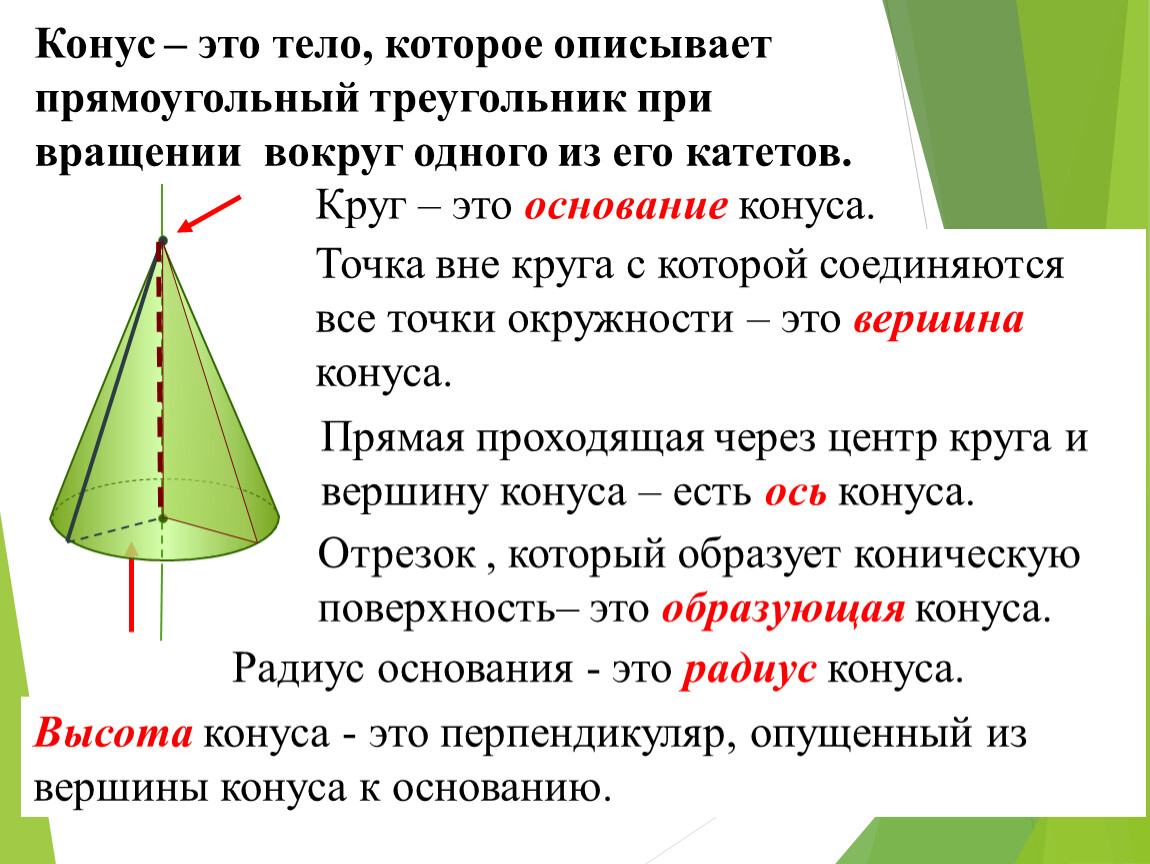
Конус — это трёхмерная геометрическая фигура с круглым основанием и вершиной, не лежащей в одной плоскости с этим основанием. Такое тело ограничено не только поверхностью, но и высотой, что делает его уникальным объектом для изучения и применения в различных областях науки и техники.

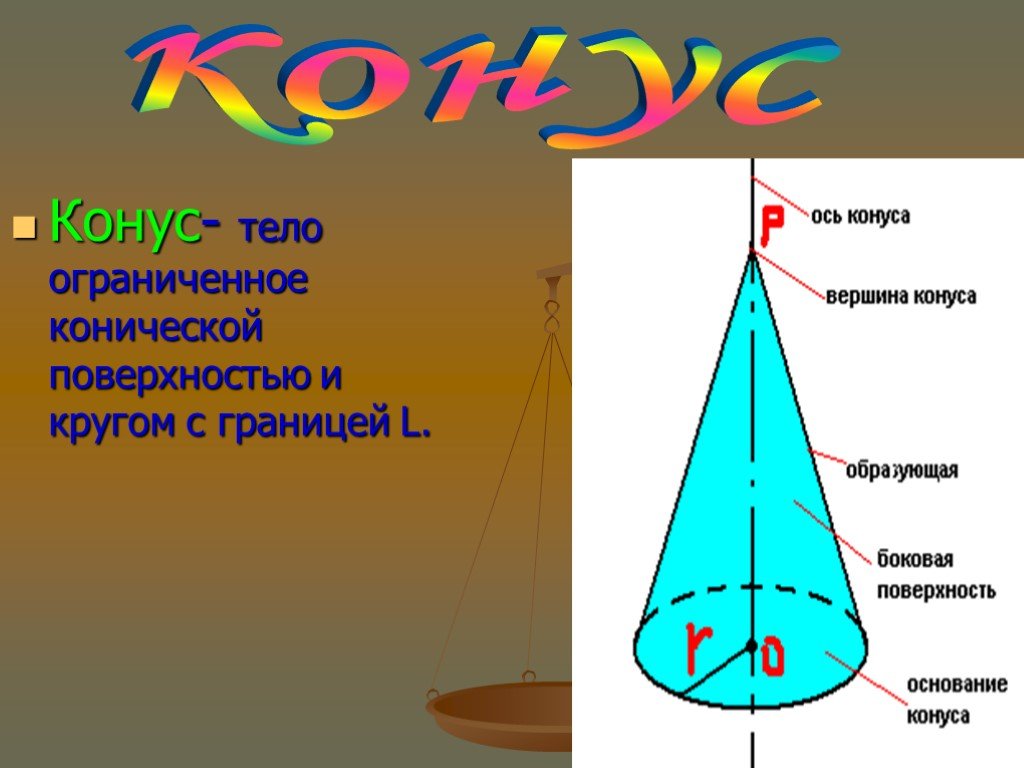
При изучении геометрических тел важно понимать, что конус имеет только одну ось симметрии, что облегчает его анализ и использование в различных задачах.

Конус. 11 класс.


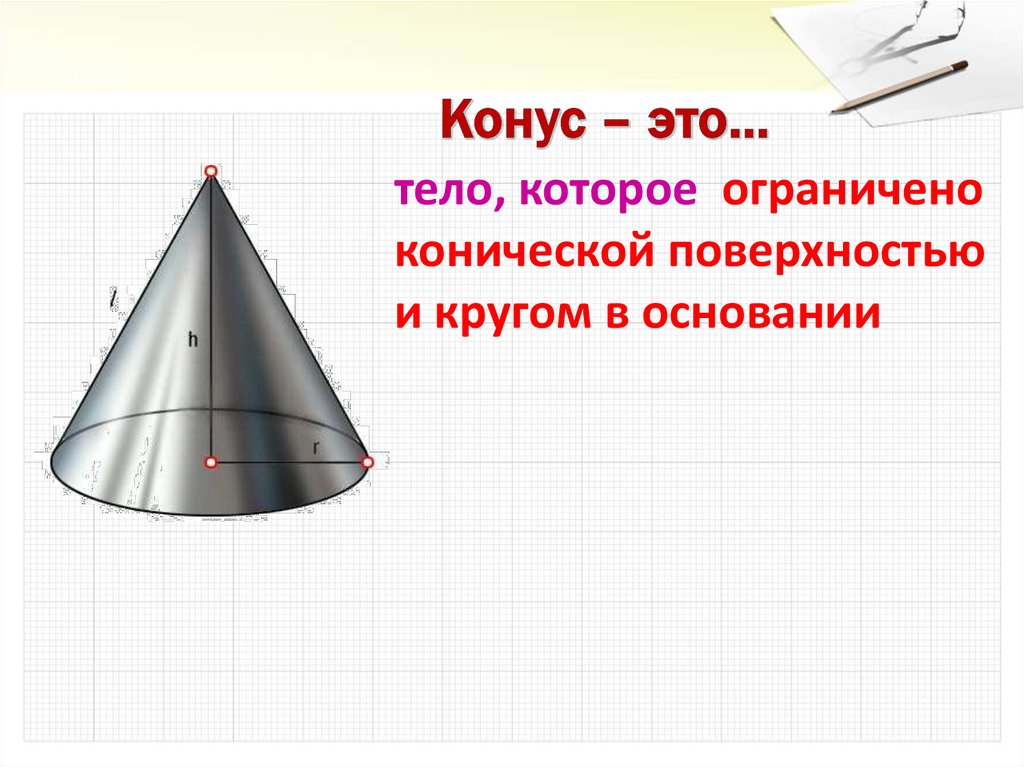
Для точных расчётов объёма конуса используйте формулу: V = (1/3) * π * r² * h, где r — радиус основания, h — высота.

Конус - Геометрия 7-9 класс #125 - Инфоурок
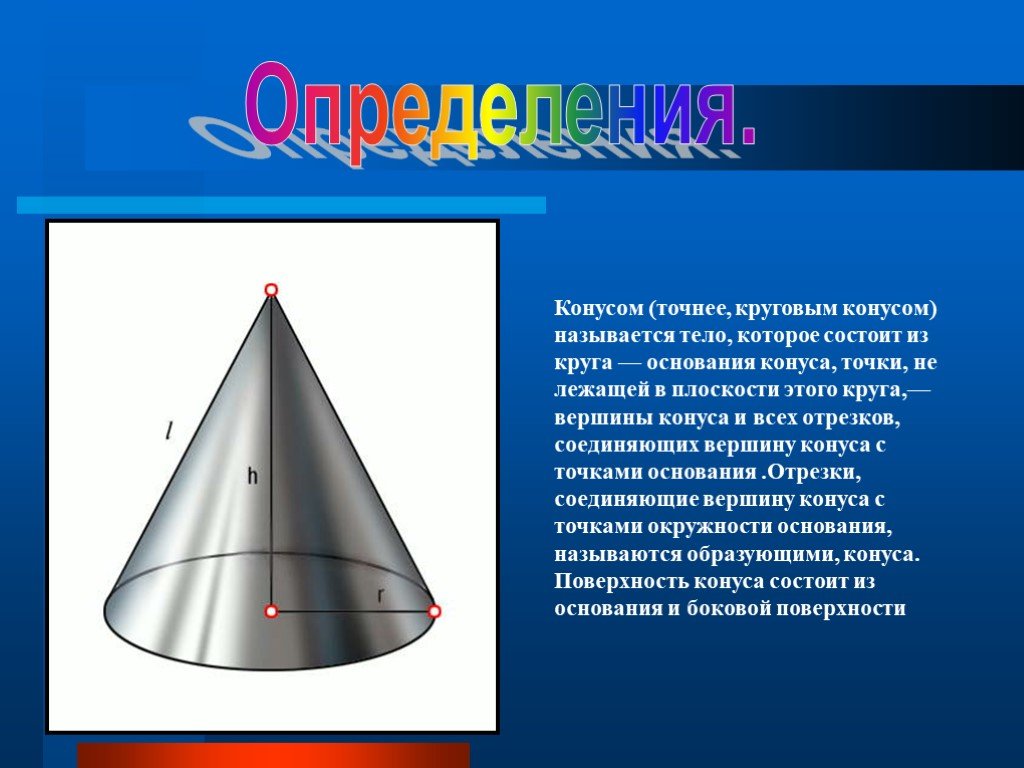
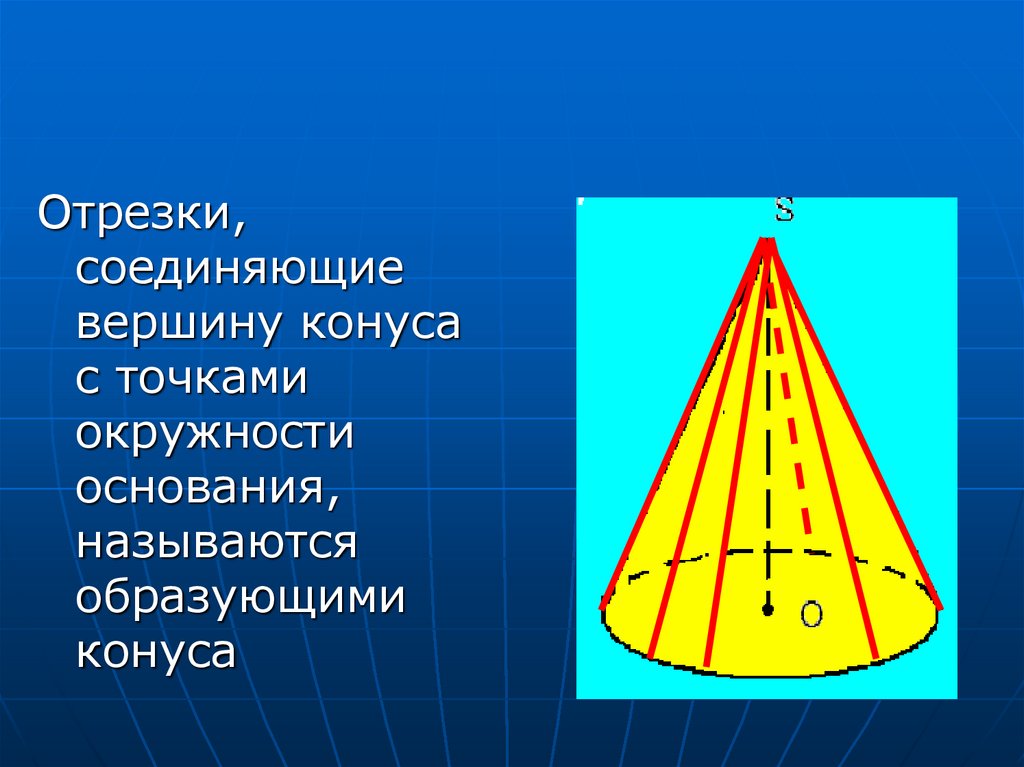
Обратите внимание, что поверхность конуса состоит из двух частей: основания (круг) и боковой поверхности, которая является частью конусообразной поверхности.

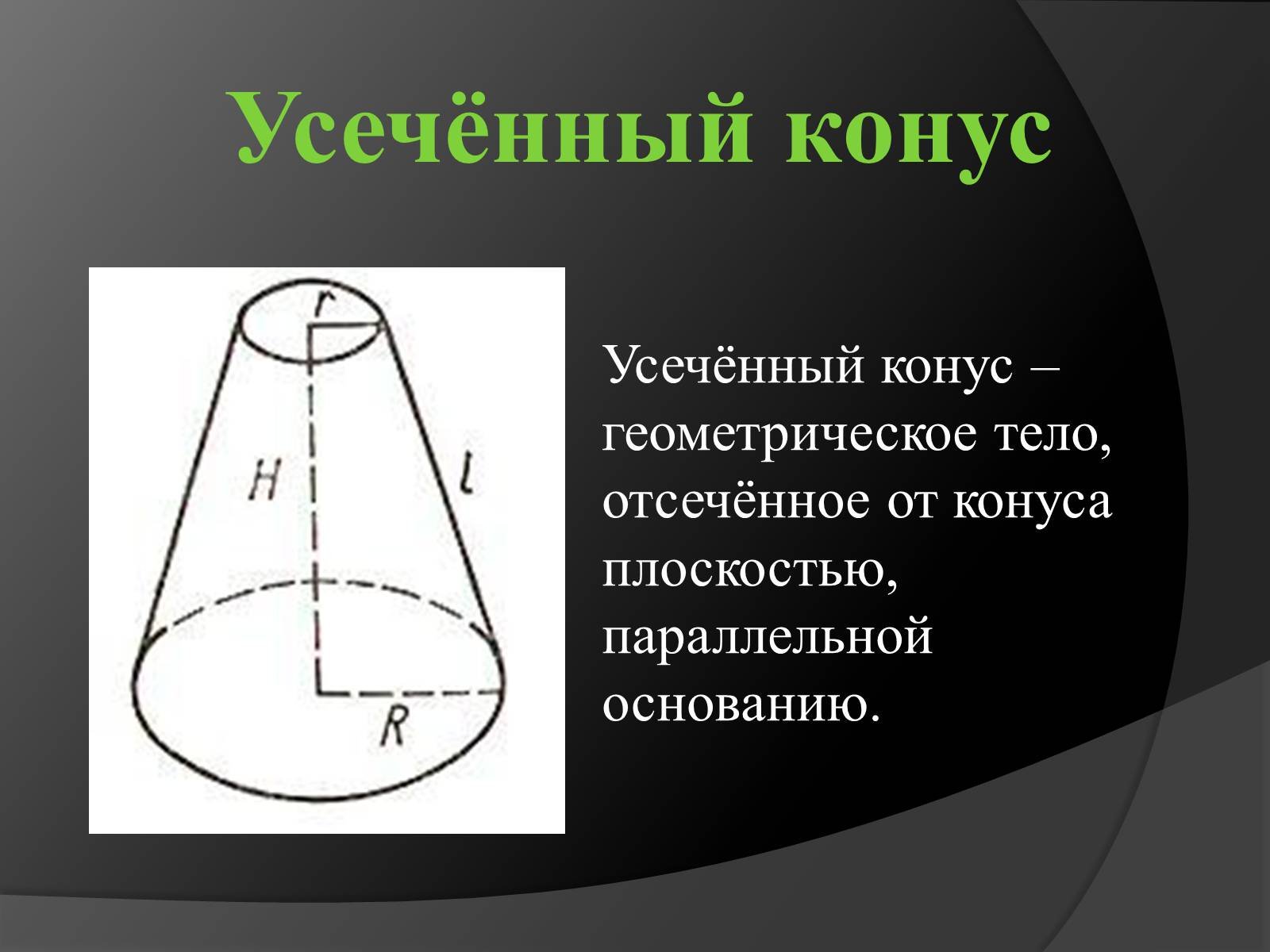
Усеченный конус ч.1 Развертка усечённого конуса.

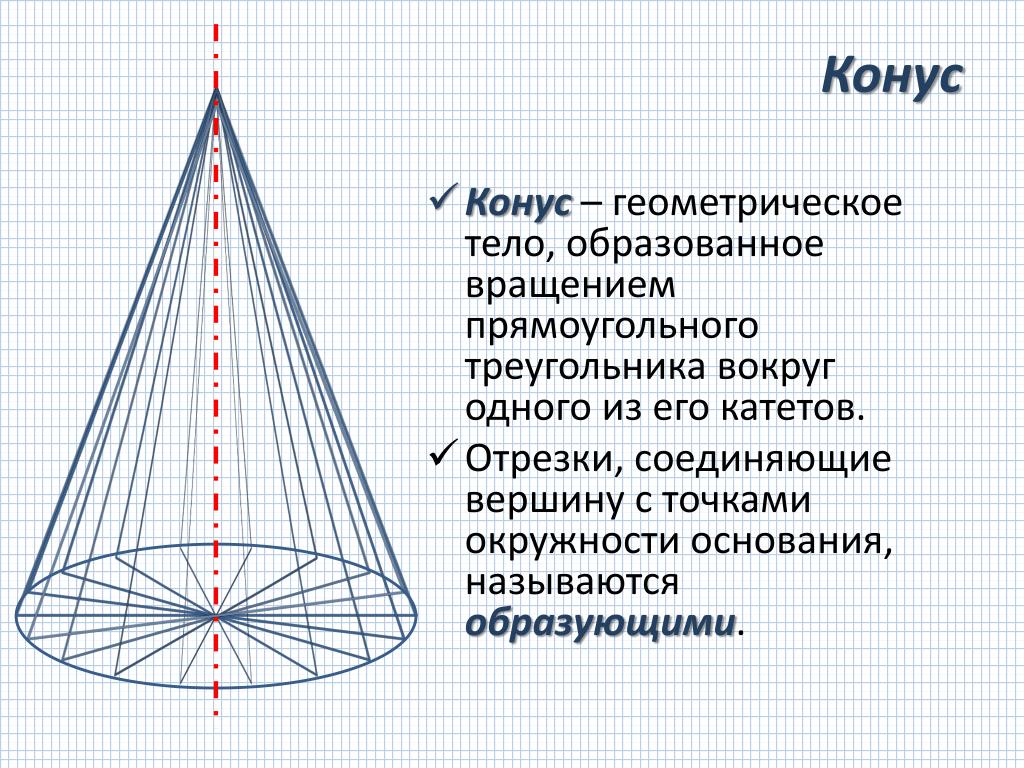
При проектировании объектов, имеющих форму конуса, учитывайте, что конус отличается от пирамиды наличием круглого основания, что делает его более устойчивым в некоторых приложениях.

ГЕОМЕТРИЯ 11 класс: Конус Площадь конуса. Усеченный конус

Для создания точных моделей конусов в 3D-графике важно задать не только радиус основания, но и правильную высоту, которая определяет угол наклона боковой поверхности.

Решение задач на конус
В архитектуре конусные элементы часто используются в куполах, башнях и других конструкциях, обеспечивая эстетику и функциональность.
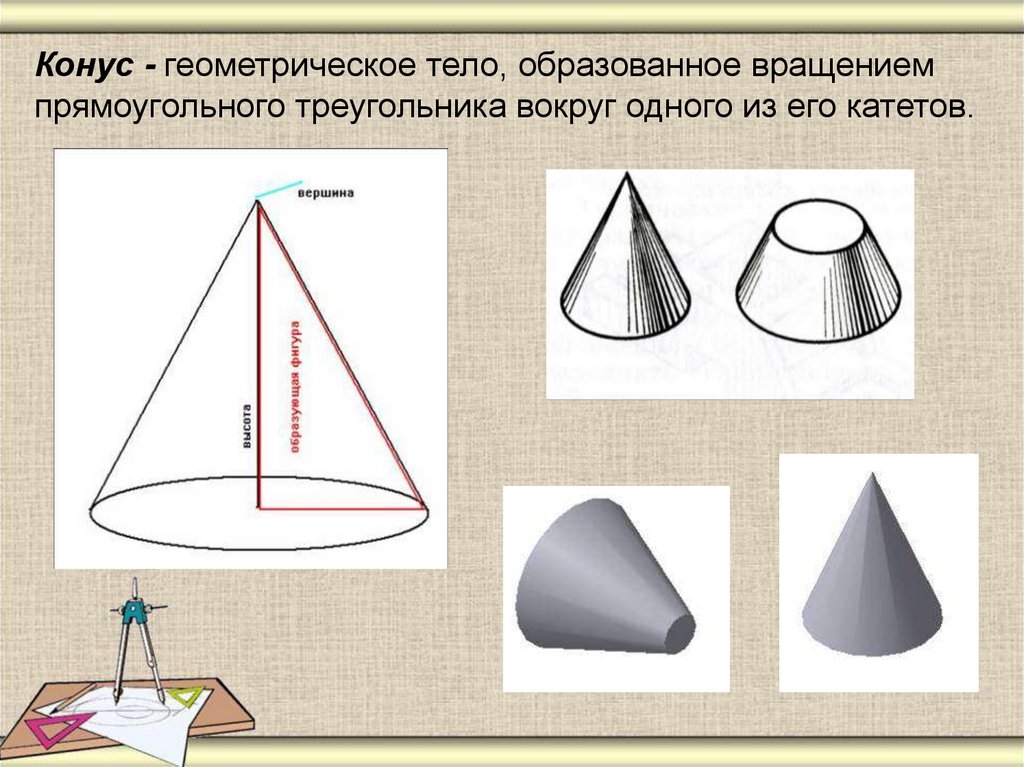
Не забывайте, что конус — это фигура с одним из самых простых и красивых геометрических описаний, что делает его идеальным объектом для обучения геометрии.

Построение развёртки конуса. Быстрый и точный способ.
Используйте конусные формы в дизайне и искусстве, чтобы добавить динамичности и выразительности вашим проектам.

Жангужина Р. К. преподаватель математики_Тема Конус и ее элементы
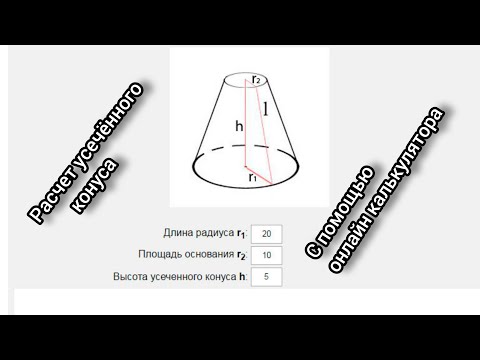
Жестяные работы. Усечённый конус. Расчет усечённого конуса с онлайн калькулятора - ссылка⬇️
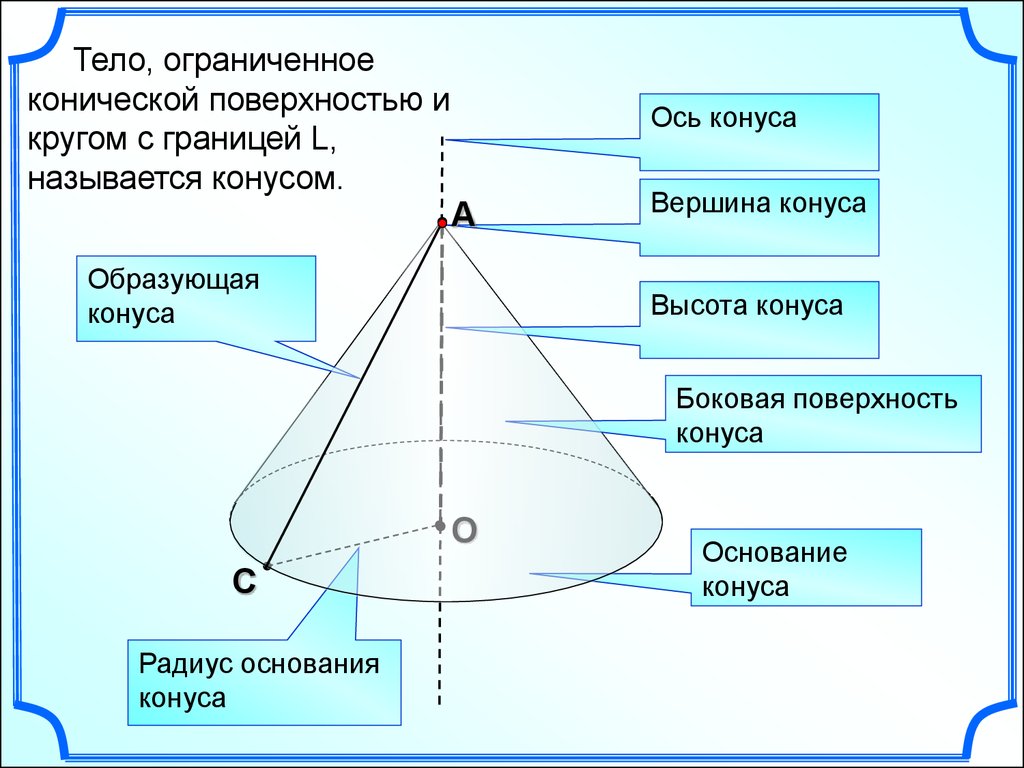
Если вам нужно построить развертку конуса, вспомните, что её можно представить как сектор круга, радиус которого равен образующей конуса.

Конус - Математика
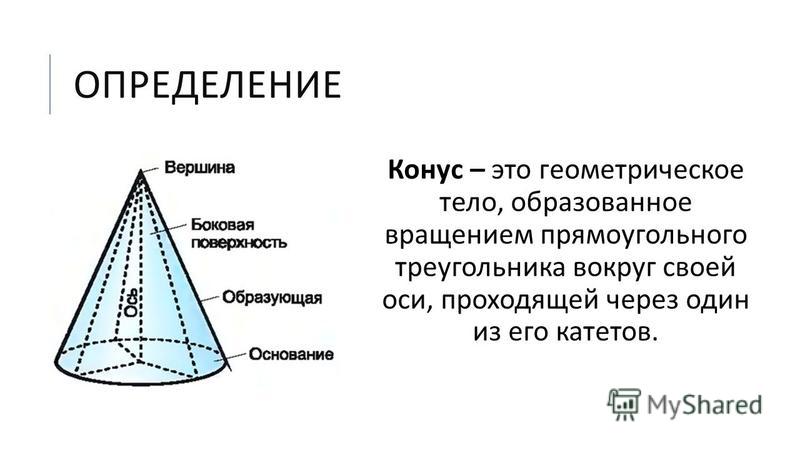

Понимание свойств конуса помогает не только в геометрии, но и в решении прикладных задач, таких как проектирование различных механизмов и сооружений.

Конус