Как быстро и точно определить расстояние между двумя точками в геометрии и на графиках
Вычисление расстояния между точками — важная задача в математике и геометрии, которая находит применение в самых различных областях. Знание различных методов позволяет быстро решать задачи, связанные с координатами точек и определением их взаимного положения. На этой странице вы найдете полезные советы и примеры, как вычислить расстояние между точками на плоскости или в пространстве.

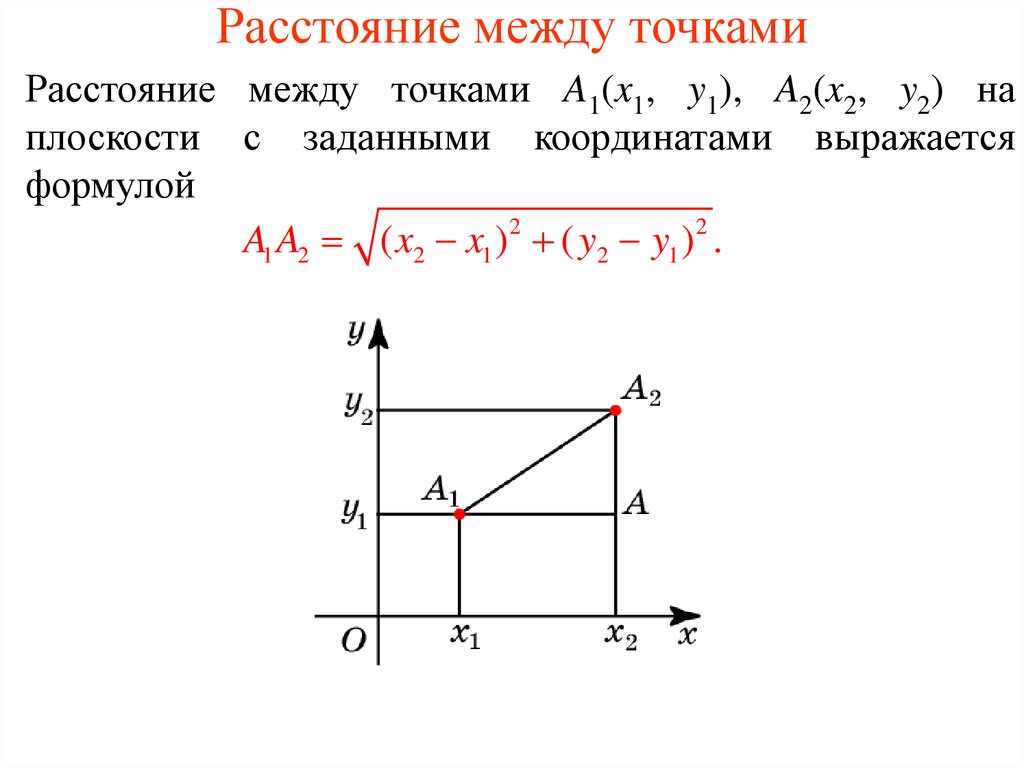
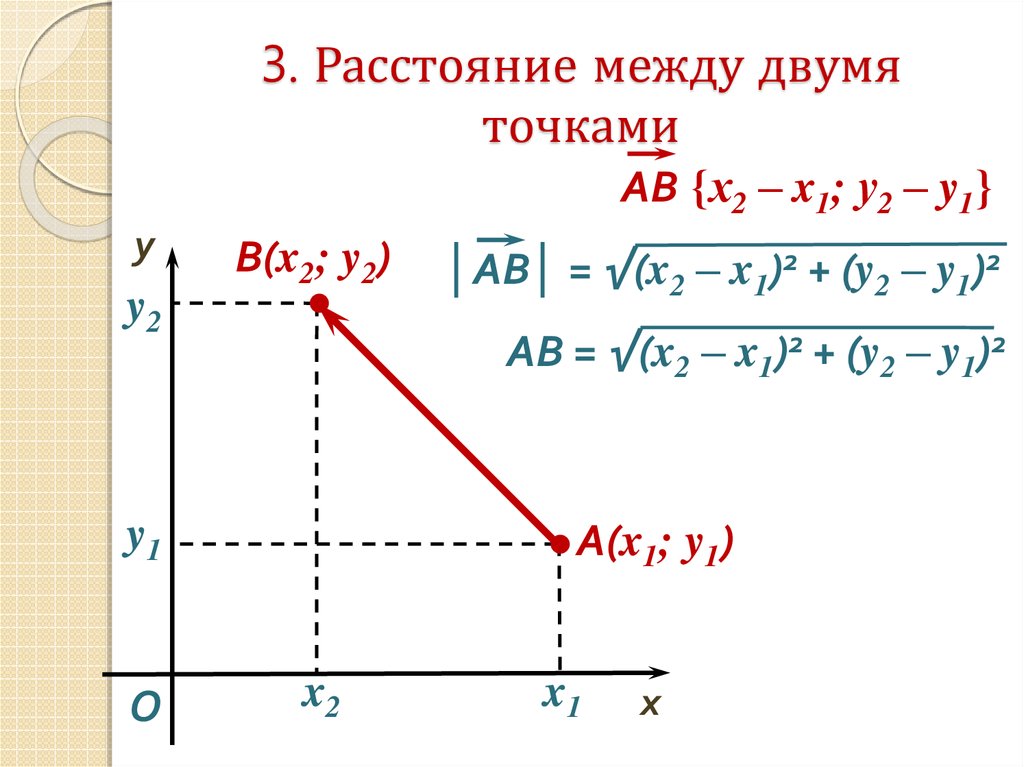
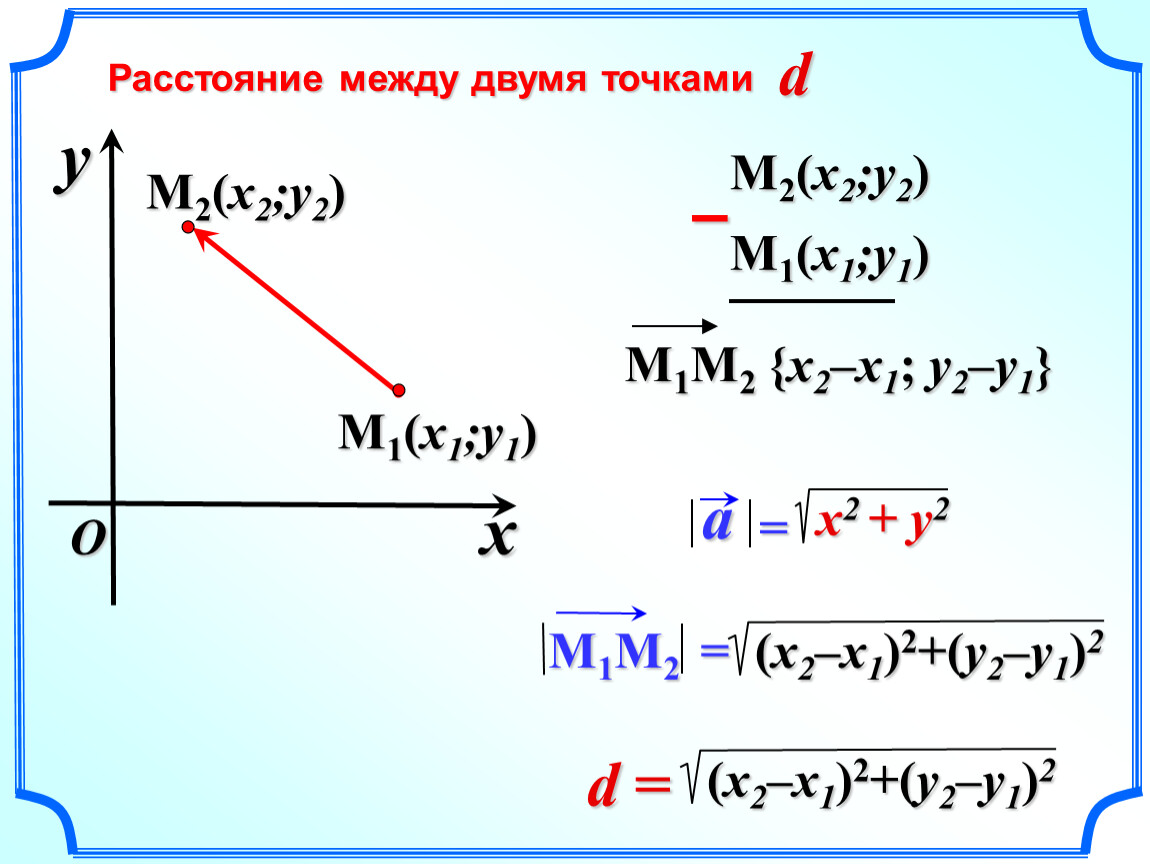
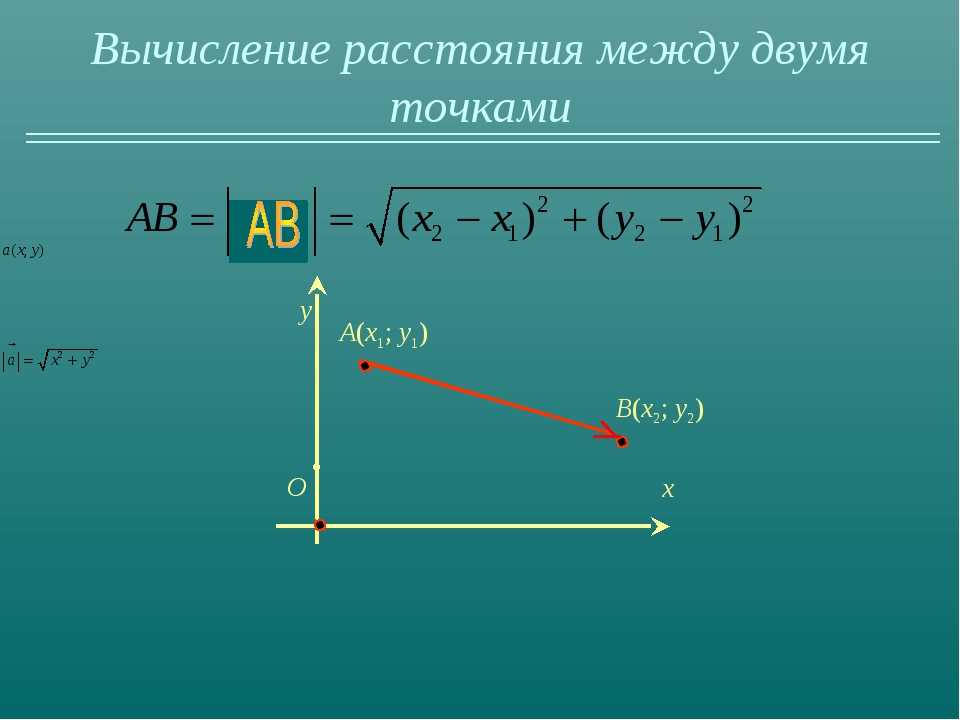
Для вычисления расстояния между двумя точками на плоскости используйте формулу: √((x2 - x1)² + (y2 - y1)²), где (x1, y1) и (x2, y2) — координаты точек.

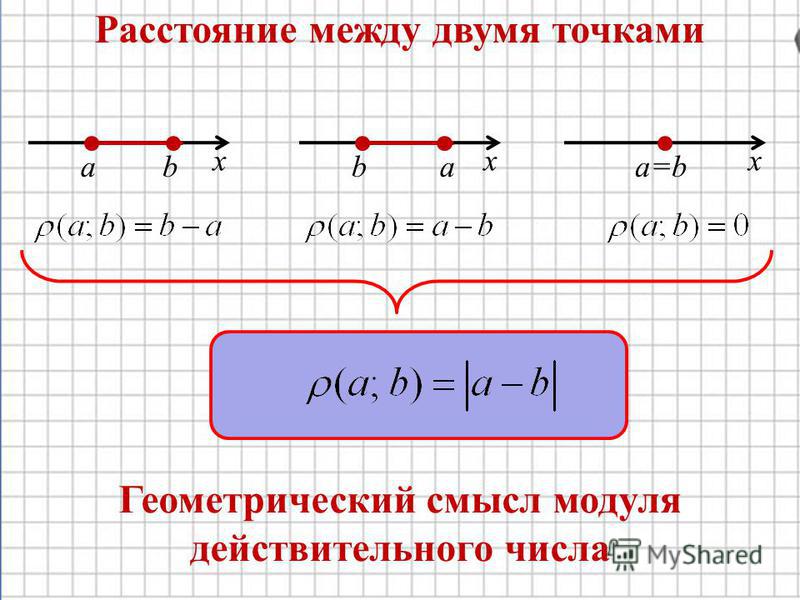
Математика 6 класс. Расстояние между точками координатной прямой
Для определения расстояния между точками в трехмерном пространстве используйте расширенную формулу: √((x2 - x1)² + (y2 - y1)² + (z2 - z1)²).

Определение широты и долготы
Чтобы найти расстояние между точками на графике, можно использовать ту же формулу, что и для плоскости, но важно правильно учитывать масштаб осей координат.
Расстояние между точками - это просто теорема Пифагора


Если точки расположены в системе координат с учетом углов, используйте формулу расстояния, основываясь на косинусах углов между векторами.

Определение расстояния между двумя точками на Земле (Между координатами) с помощью python
Проверяйте точность расчетов, особенно если работаете с координатами, полученными вручную или через сложные вычисления.
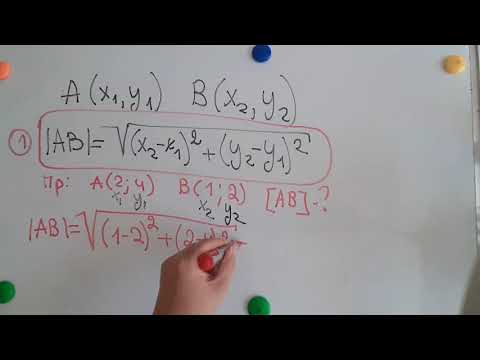
Расстояние между точками

Для быстрого вычисления расстояний используйте онлайн-калькуляторы, которые автоматически подставляют координаты и рассчитывают результат.

Если вам нужно определить кратчайшее расстояние от точки до прямой, используйте формулу расстояния от точки до линии в аналитической геометрии.

Расстояние между двумя точками. Координаты середины отрезка.
Если задача касается расстояния между точками на сфере, используйте сферическую геометрию и формулы, учитывающие кривизну поверхности.

Расстояние между точками координатной прямой. Математика 6 класс

Определение расстояния по угловой величине


При вычислении расстояния важно правильно учитывать единицы измерения, чтобы результат был корректен и соответствовал поставленной задаче.

4 класс, 40 урок, Расстояние между точками координатного луча


Для решения сложных задач с множественными точками применяйте методы векторной алгебры и теоремы Пифагора для упрощения вычислений.

Расстояние от точки до плоскости / Вывод формулы
