Методы вычисления площади под кривой на графике функции с примерами
На данной странице вы найдете полезные советы и пошаговые инструкции по нахождению площади закрашенной фигуры на графике функции. Мы рассмотрим основные методы интегрирования и научим, как применить их для решения задач на вычисление площади. Изучив эти методы, вы сможете без труда находить площади под кривыми, используя графики и математические инструменты.

Перед тем как найти площадь закрашенной области, важно правильно определить границы интегрирования, которые определяются точками пересечения графика функции с осями координат.

Как относится площадь закрашенных фигур к площади прямоугольника

Если функция имеет несколько областей, заключенных между графиком и осью, каждая такая область должна быть посчитана отдельно с учетом знаков.

Площадь фигуры

При вычислении площади под графиком важно помнить, что для нахождения площади нужно использовать определенный интеграл, который помогает учесть все изменения функции в пределах отрезка.
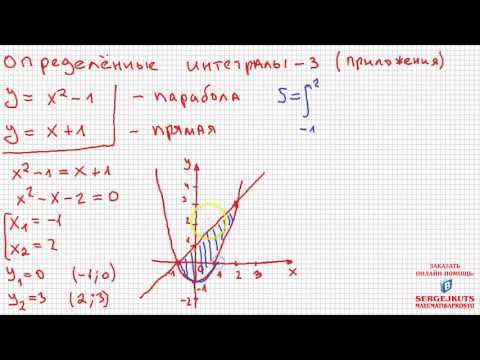
Математика без Ху%!ни. Определенные интегралы, часть 3. Площадь фигуры.
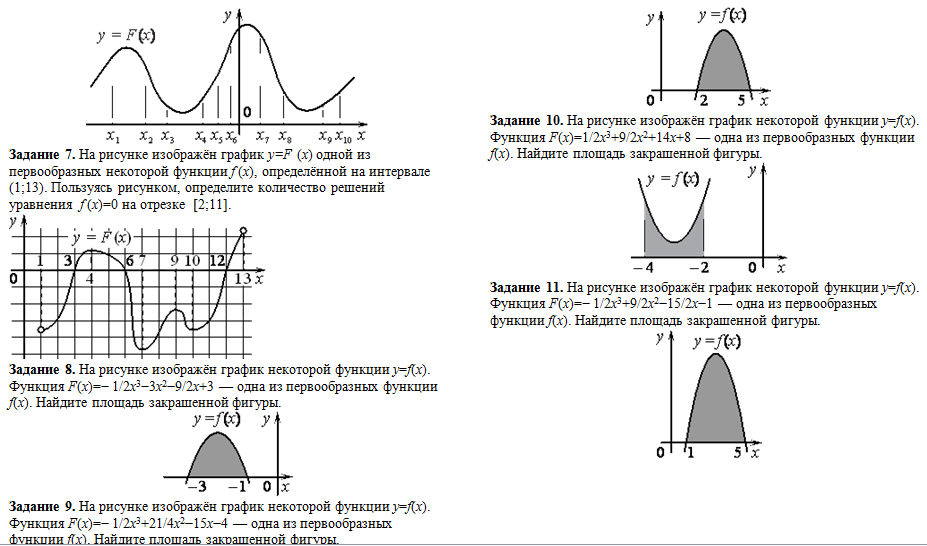
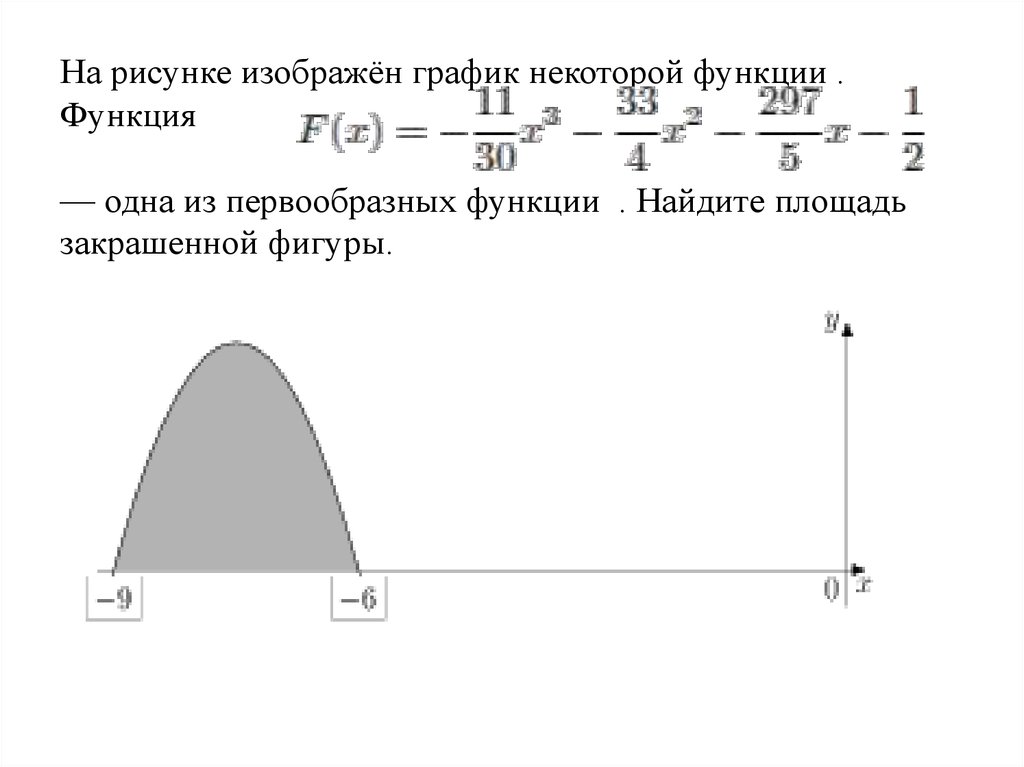
Если график функции сложный, полезно разбиение на более простые части с последующим нахождением площади для каждой из них и сложением результатов.
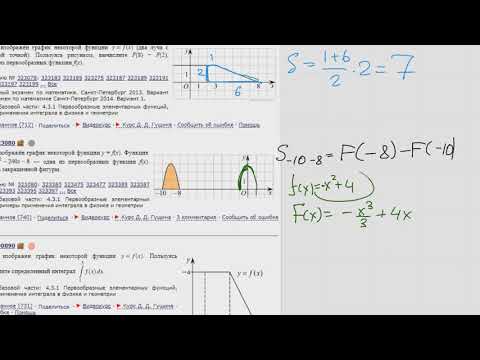
ЕГЭ Математика профиль Задание 7 #323080

При наличии нескольких функций, которые ограничивают область, площадь можно найти как разницу интегралов между верхней и нижней функцией.

Смысл интеграла и производной. В помощь студенту

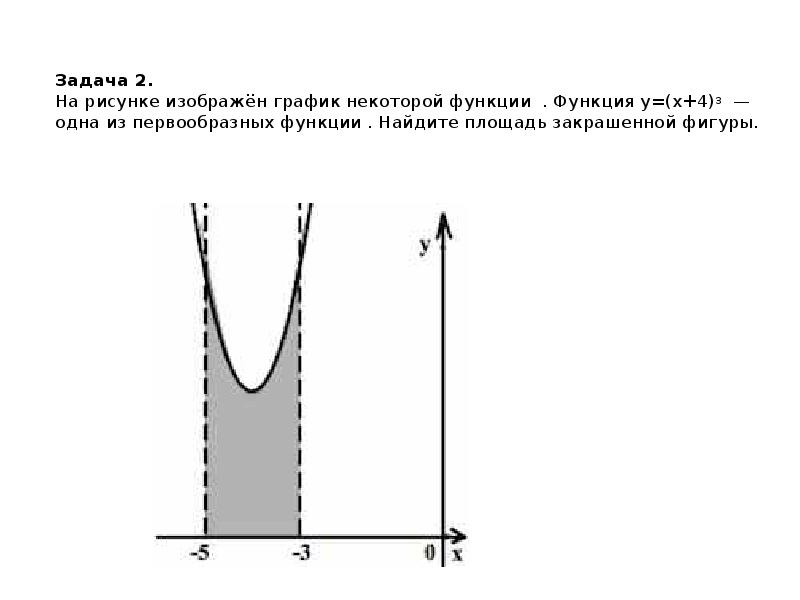
Если функция имеет горизонтальные асимптоты, не забудьте учесть их в расчетах, так как они могут влиять на границы интегрирования.
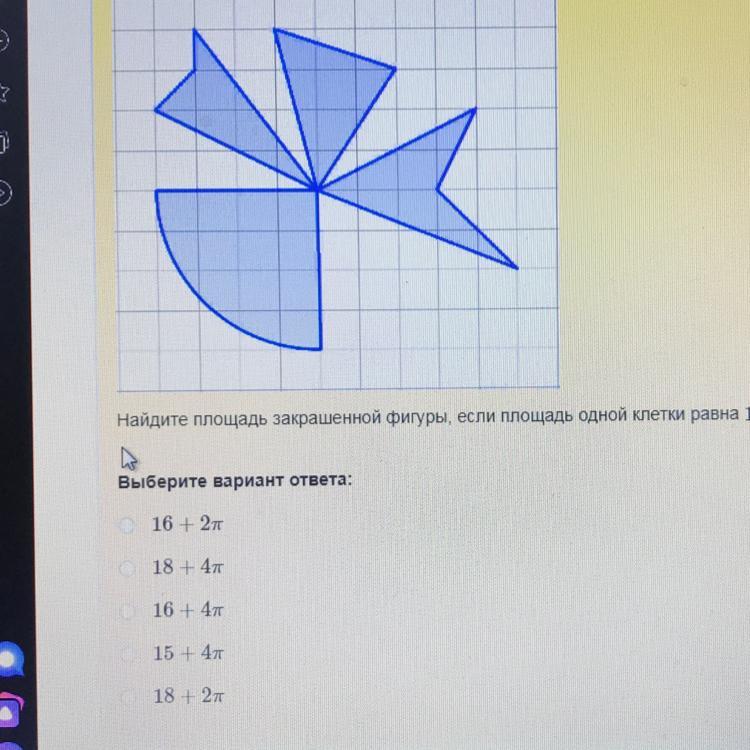
Для нахождения площади между двумя функциями можно использовать метод вычисления площади между кривыми с помощью интегралов от разности функций.
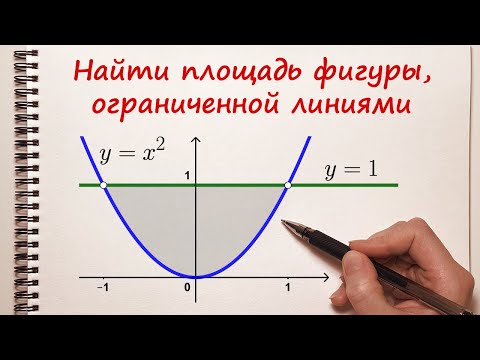
Найти площадь фигуры, ограниченной линиями. Пример 1.


Если функция имеет экстремумы, рекомендуется сначала провести анализ поведения функции в этих точках для точного определения области, ограниченной графиком.
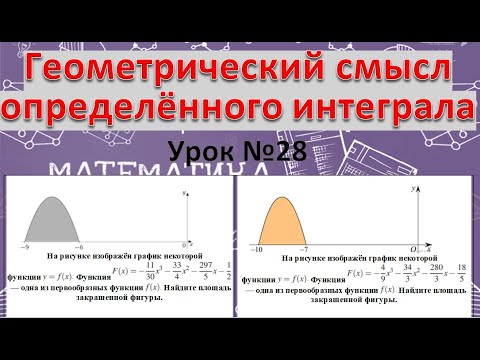
На рисунке изображён график функции f(x).F(x) -первообразная f(x) Найдите площадь закрашенной фигуры
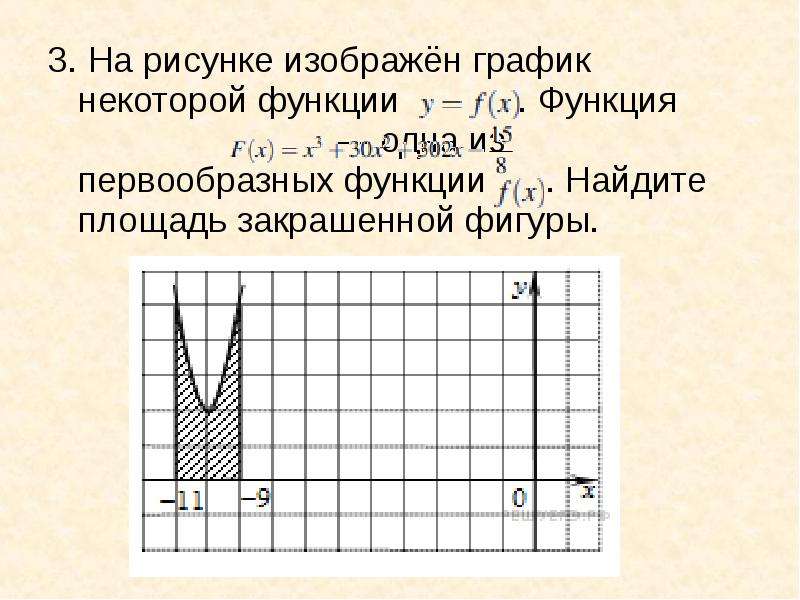

Использование численных методов интегрирования, таких как метод трапеций или метод Симпсона, может быть полезно, если аналитическое вычисление площади затруднительно.
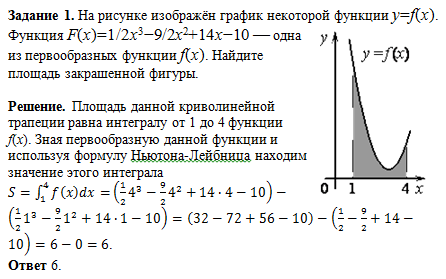
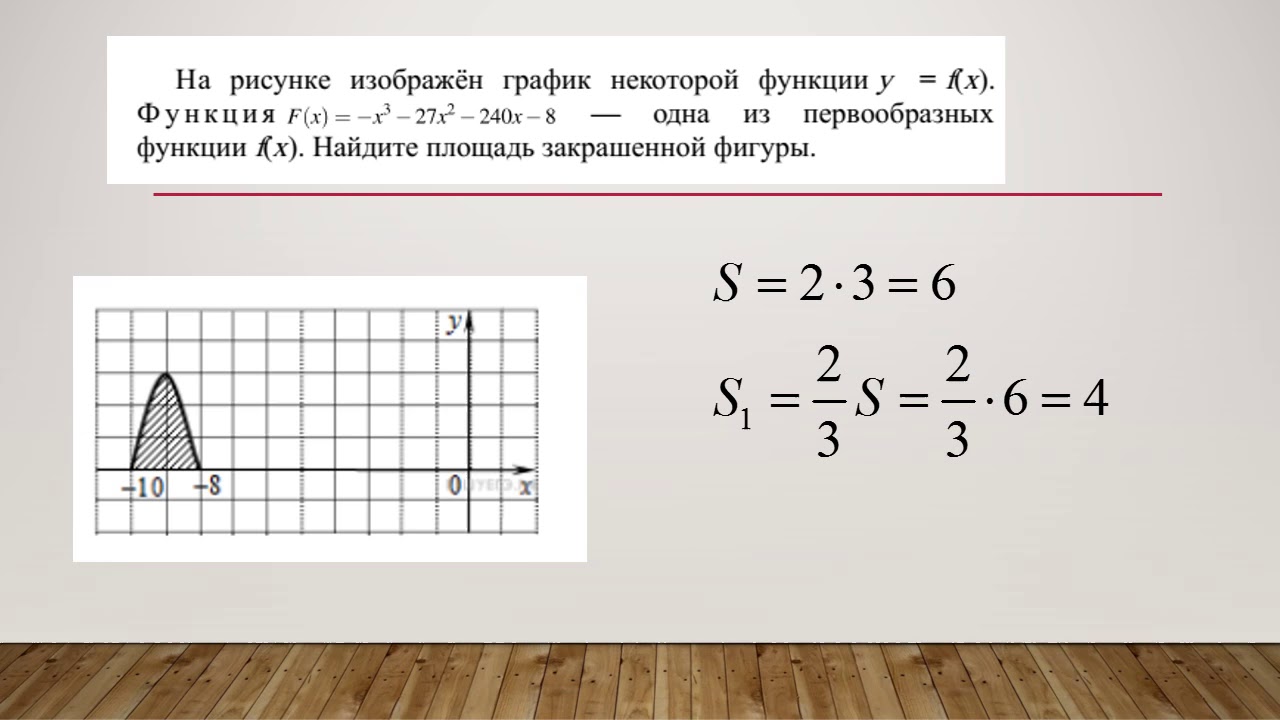
При решении задач важно проверять корректность полученного результата, используя графический калькулятор или онлайн-инструменты для построения графиков функций.

Найдите площадь закрашенной фигуры.