Алгоритм Уоршалла: шаг за шагом к созданию матрицы достижимости
Алгоритм Уоршалла — это метод для нахождения матрицы достижимости в ориентированных графах. Он позволяет вычислять, какие вершины достижимы из других в графах, что полезно для анализа связности и оптимизации путей. В этой подборке мы собрали полезные советы, примеры и фотографии, чтобы сделать ваше освоение алгоритма более простым и понятным.

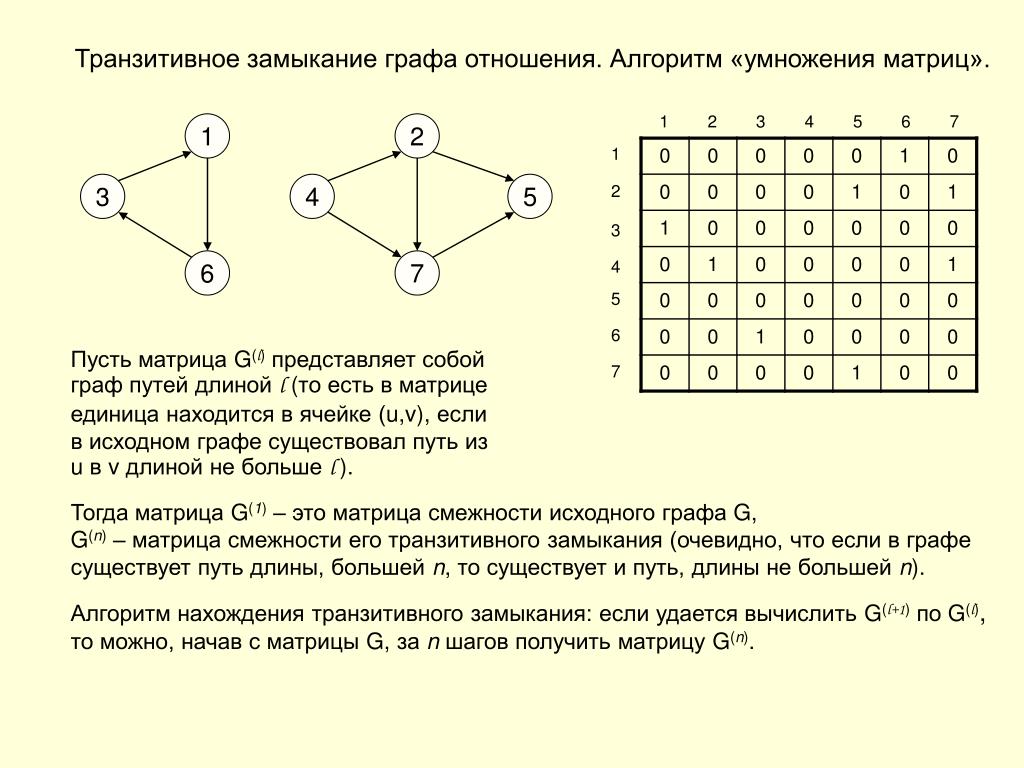
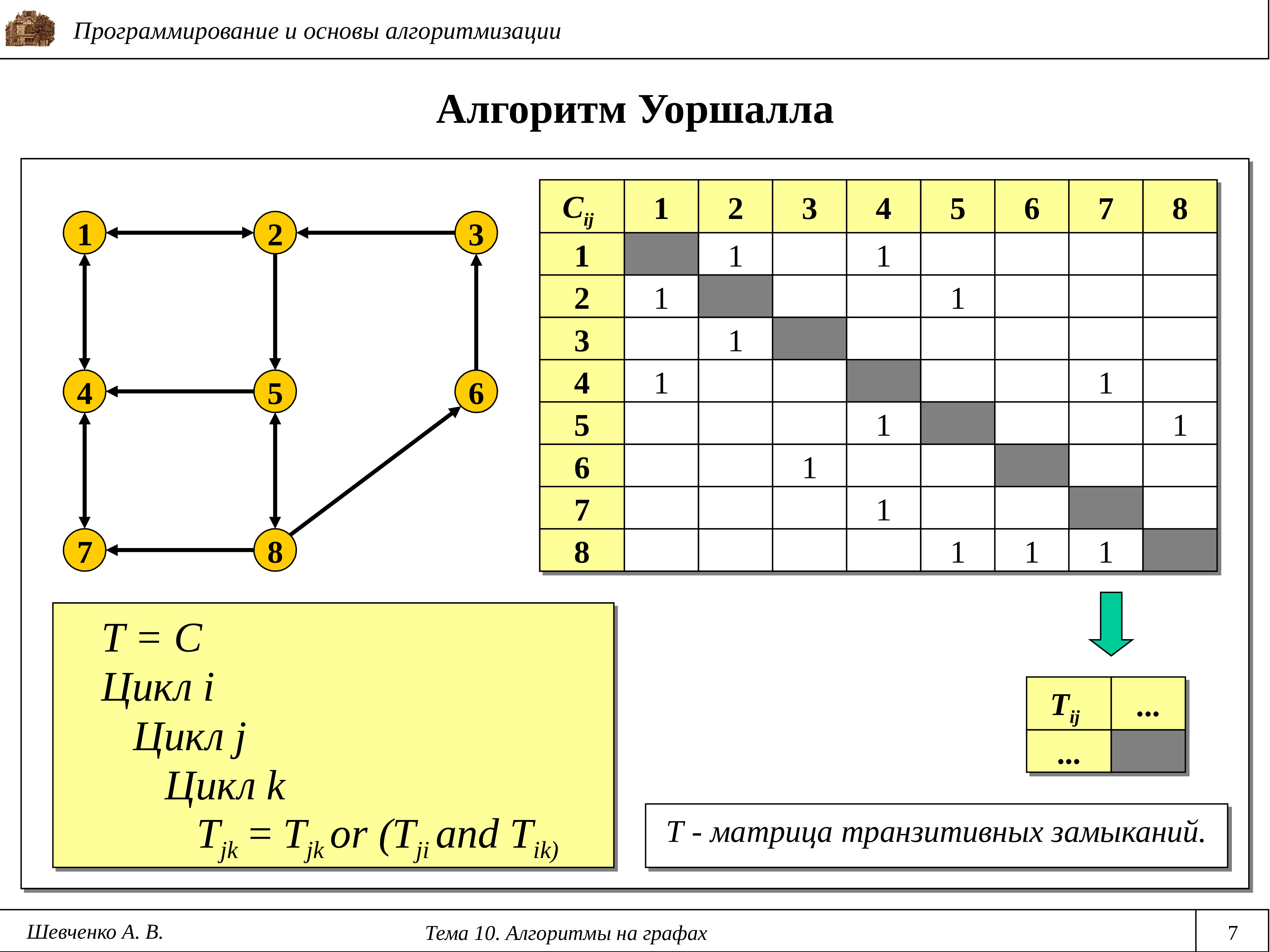
Перед началом работы с алгоритмом Уоршалла убедитесь, что ваша матрица достижимости правильно сформирована. Начните с заполнения её единицами и нулями в соответствии с наличием или отсутствием ребер между вершинами.
Инсультка жеткирбей озубузду кароо:Озубуздон Неохакинг практика

Важно понимать, что алгоритм Уоршалла работает только для ориентированных графов, так как рассматривает направления связи между вершинами, что делает его эффективным для анализа транспортных и информационных сетей.

Алгоритм Флойда

Алгоритм Уоршалла можно модифицировать для работы с графами с весами, если добавлять условие для минимизации пути между вершинами в процессе вычислений.

ОДНОГРУППНИКАМ матрица достижимости и возведение её в степень
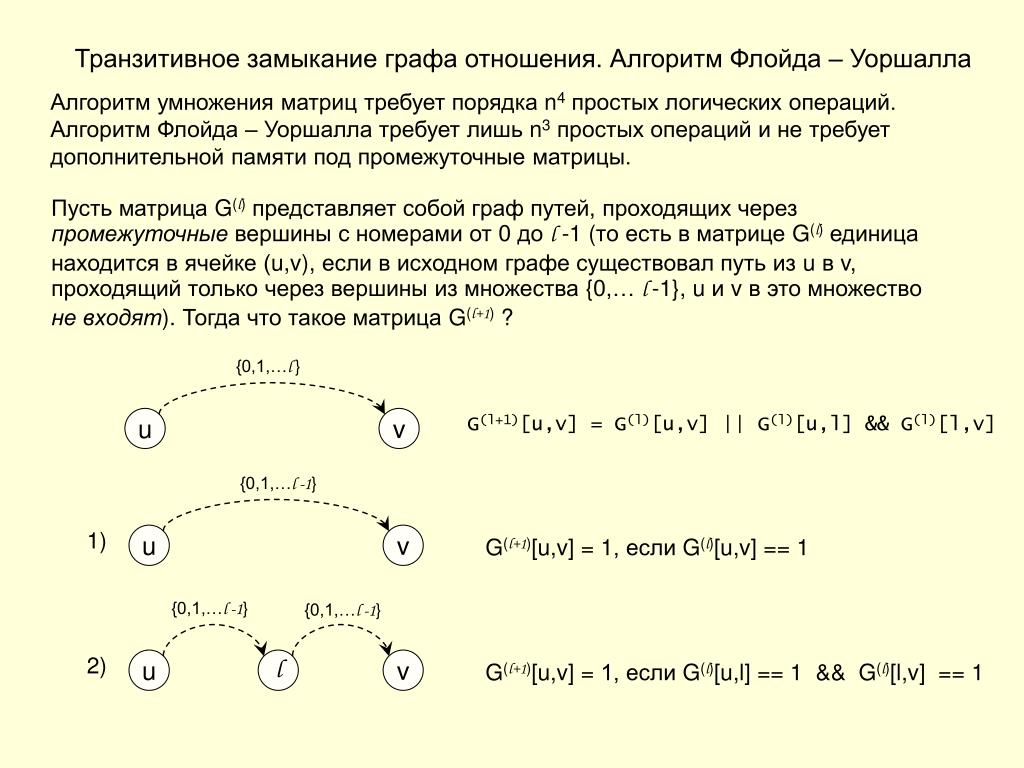
Постарайтесь тщательно отследить шаги алгоритма, особенно если работаете с большими графами. Это поможет избежать ошибок при вычислении матрицы достижимости и ускорит решение задач.

Алгоритм Флойда


Для удобства работы с матрицами можно использовать программные средства, такие как Python с библиотеками NumPy или Graph-tool, что ускорит выполнение алгоритма.

Достижимость в графах
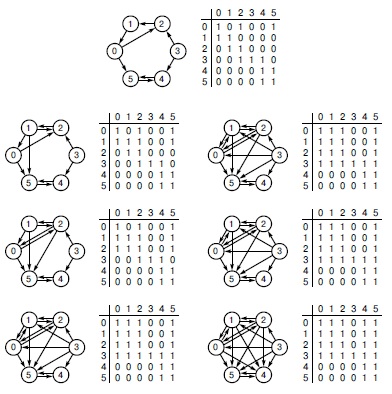

При реализации алгоритма Уоршалла важно правильно обновлять матрицу достижимости на каждом шаге, иначе результат может быть некорректным, и вам нужно будет повторить вычисления.
Поиск расстояния между всеми парами вершин. Алгоритм Уоршалла-Флойда
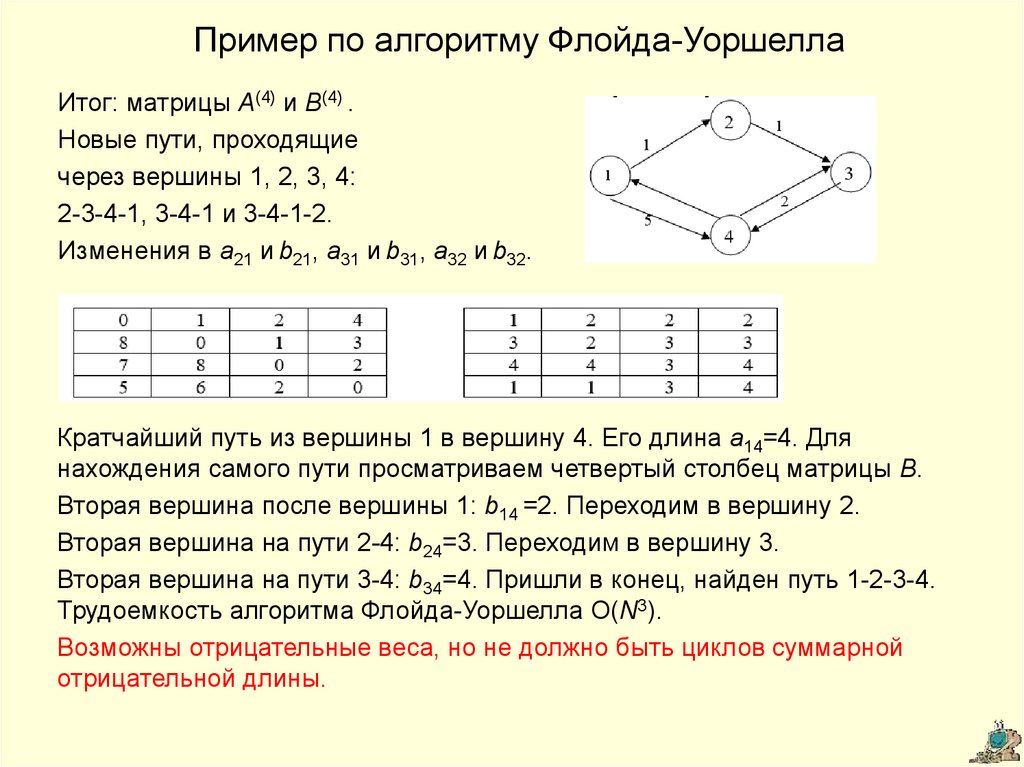
Если вам нужно проанализировать несколько различных графов, всегда старайтесь нормализовать данные в матрицах, чтобы результаты можно было легко сравнивать между собой.
Не забывайте, что алгоритм Уоршалла можно эффективно использовать не только для вычисления матрицы достижимости, но и для нахождения кратчайших путей между вершинами.
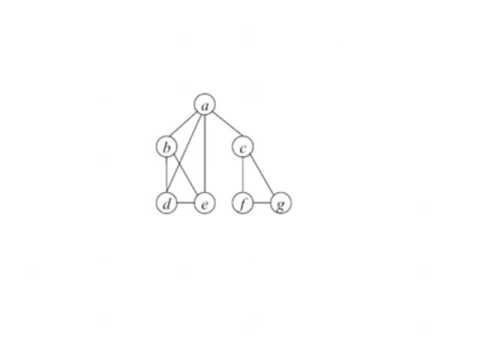
Обход графа в глубину

Регулярно проверяйте промежуточные результаты, чтобы не пропустить возможные ошибки в процессе выполнения алгоритма. Это важно, особенно при работе с большими объемами данных.

Достижимость в графах

Понимание принципов работы алгоритма Уоршалла и матрицы достижимости поможет вам более эффективно решать задачи в области теории графов и оптимизации, такие как маршрутизация и планирование.

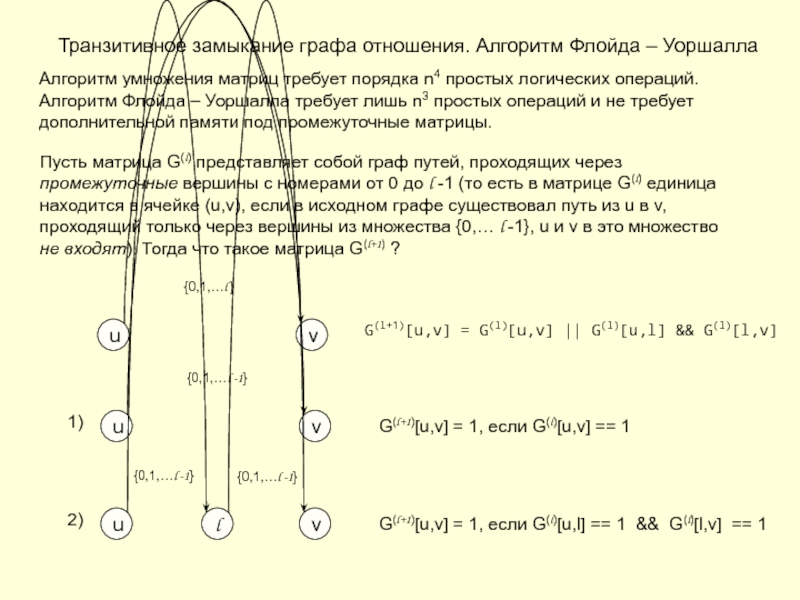
Идея алгоритма Флойда-Уоршелла



Алгоритм Уоршелла