Алгебраическое решение неравенств: эффективные техники и важные советы
Алгебраический способ решения неравенств — это мощный инструмент, который позволяет решить многие математические задачи, используя базовые операции с переменными и числами. В этой подборке мы рассмотрим основные принципы и шаги, которые помогут вам разобраться в методе и применить его на практике.


Перед началом решения неравенства всегда упрощайте его, если это возможно. Приведите подобные слагаемые и раскрывайте скобки, чтобы упростить выражение.
МЕТОД ИНТЕРВАЛОВ 😀 #егэ #математика #профильныйегэ #shorts #огэ

Не забывайте о знаках неравенств: при умножении или делении на отрицательное число, знак неравенства меняется на противоположный.

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства - TutorOnline

Будьте внимательны при работе с дробями: для того, чтобы избавиться от знаменателя, умножьте обе части неравенства на его наименьшее общее кратное.
СИСТЕМА НЕРАВЕНСТВ 😉 #егэ #математика #профильныйегэ #shorts #огэ


Если неравенство содержит абсолютные значения, разделите его на два случая: один для положительных значений, другой — для отрицательных.

Метод интервалов - Как решить неравенство методом интервалов - Алгебра 9 класс - МегаШкола
Не забывайте проверять конечные решения на принадлежность исходному неравенству, особенно если вы использовали операции, которые могут изменить область допустимых значений.

Решение неравенства методом интервалов

Если вы сталкиваетесь с многочленами, старайтесь искать корни уравнений, чтобы затем определить интервалы, на которых неравенство выполняется.
Используйте графический метод для проверки решений. Построение графиков может помочь визуализировать решение неравенства и быстрее найти правильный ответ.

Метод интервалов #4 для продвинутых
При решении неравенств с переменными в числителе и знаменателе учитывайте области, где выражения могут быть неопределены (например, деление на ноль).

ПРОСТЕЙШИЙ метод решения систем квадратных неравенств

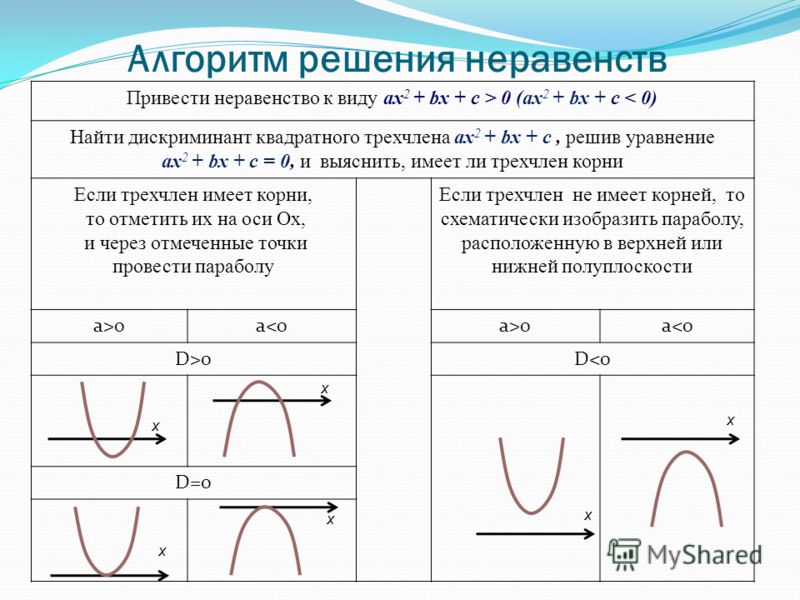
Решение квадратных неравенств методом интервалов. 8 класс.

Используйте логические преобразования для сложных неравенств. Это помогает сократить время на решение и избежать ошибок при работе с несколькими операциями одновременно.

Постепенно усложняйте задачи, начиная с простых неравенств, чтобы понять все нюансы алгебраического метода, прежде чем переходить к более сложным вариантам.
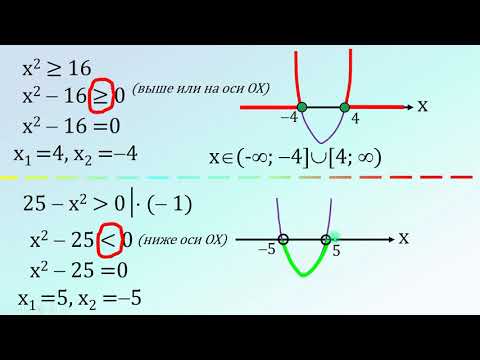
метод парабол для решения квадратных неравенств