Вычисляем параметры треугольника по длинам сторон
Подробное руководство и полезные советы для работы с треугольником, где известны длины всех сторон. Узнайте, как находить углы, площади и другие параметры.

Для начала убедитесь, что заданные стороны образуют треугольник, проверив неравенство треугольника: сумма любых двух сторон должна быть больше третьей.

ОГЭ Задание 26 Подобные треугольники


Чтобы найти углы треугольника, используйте теорему косинусов: cos(угол) = (a² + b² - c²) / (2ab), где a, b, c — стороны.

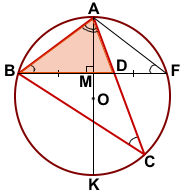
Геометрия В треугольнике ABC известны длины сторон AB = 18, AC = 36, точка O — центр окружности

Для удобства вычислений используйте калькулятор или математические программы, такие как GeoGebra или WolframAlpha.

Геометрическая задача из варианта ОГЭ


Если требуется найти площадь треугольника, примените формулу Герона: √(p(p-a)(p-b)(p-c)), где p — полупериметр (a+b+c)/2.

✓ Самая сложная задача в ОГЭ-2020 - Задание 26. Математика - Геометрия - Борис Трушин
Помните, что сумма углов любого треугольника равна 180°. Это может помочь проверить корректность расчетов.

Геометрия В треугольнике ABC известны длины сторон AB = 36, AC = 48, точка O — центр окружности
Если необходимо построить треугольник, используйте циркуль и линейку, откладывая стороны в соответствии с заданными длинами.
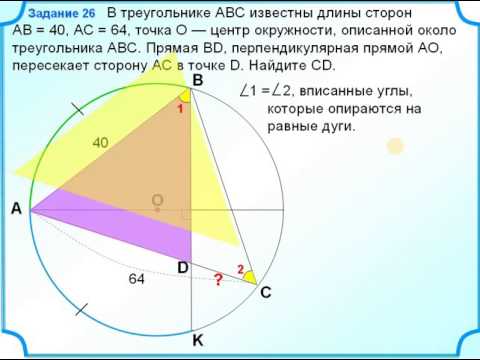
Математика ОГЭ. Задача 26_4
Для проверки правильности расчетов можете использовать онлайн-калькуляторы для треугольников.
Не забывайте про единицы измерения: длины сторон и углы должны быть в одной системе для корректных расчетов.

Решение задания №25 варианта 1 из ОГЭ по математике Ященко 36 вариантов ФИПИ 2023 Ответы ГДЗ
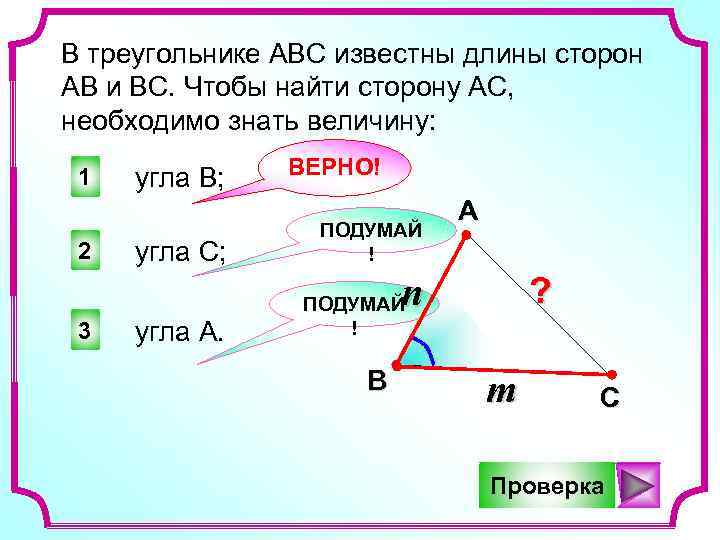
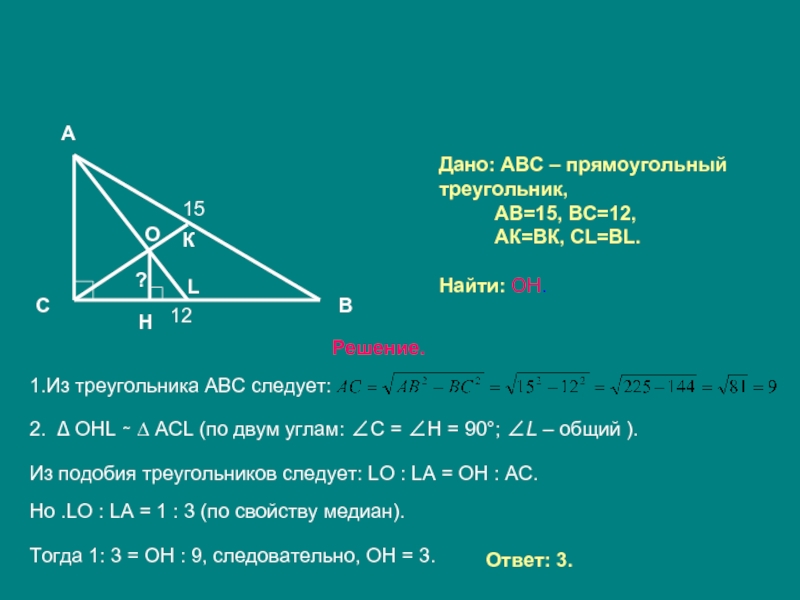
Изучите свойства прямоугольных треугольников, если одна из сторон оказывается гипотенузой. В таком случае можно использовать теорему Пифагора.

Зачем нужны синусы и косинусы?

При решении задач помните, что треугольник с заданными сторонами всегда уникален, если выполняется неравенство треугольника.

Геометрия В треугольнике АВС известны длины сторон АВ = 15 см, ВС = 14 см, АС = 13 см. точка М делит