Метод промежутков для решения уравнений с модулем: все, что нужно знать
В этом разделе мы рассмотрим, как решить уравнение с модулем с помощью метода промежутков. Это эффективная техника, которая позволяет систематически анализировать возможные решения, разделяя исходное уравнение на несколько случаев в зависимости от того, что находится под модулем. Подробное объяснение каждого шага и практические советы помогут вам легко справиться с такими задачами.


При решении уравнений с модулем всегда учитывайте, что модуль выражает расстояние от числа до нуля, поэтому его значение всегда неотрицательно.

Как решать уравнения с модулем или Математический торт с кремом (часть 1) - Математика

Для использования метода промежутков, разделите уравнение на несколько случаев в зависимости от того, чему равен выражение под модулем (положительное или отрицательное).
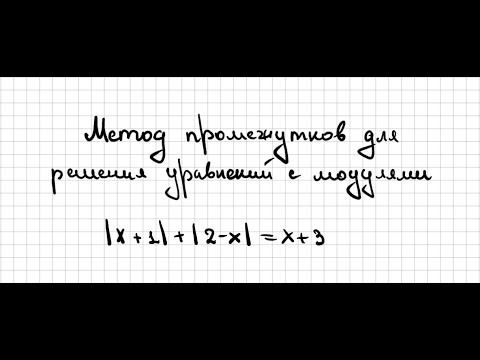
Метод промежутков для решения уравнений с модулями
Когда решаете уравнение с модулем, не забывайте, что каждая ситуация (модуль положителен или отрицателен) может привести к разным результатам.

Неравенства с модулем - Математика - TutorOnline

Перед тем как начинать решать уравнение с модулем, внимательно определите область допустимых значений, чтобы избежать ошибок при вычислениях.

УРАВНЕНИЯ С МОДУЛЕМ. Метод интервалов для решения уравнений.

Если уравнение содержит несколько модулей, решайте их поочередно, выделяя промежутки, где выражения внутри модулей меняют знак.

Метод промежутков. Уравнения с Модулем Часть 2 из 3
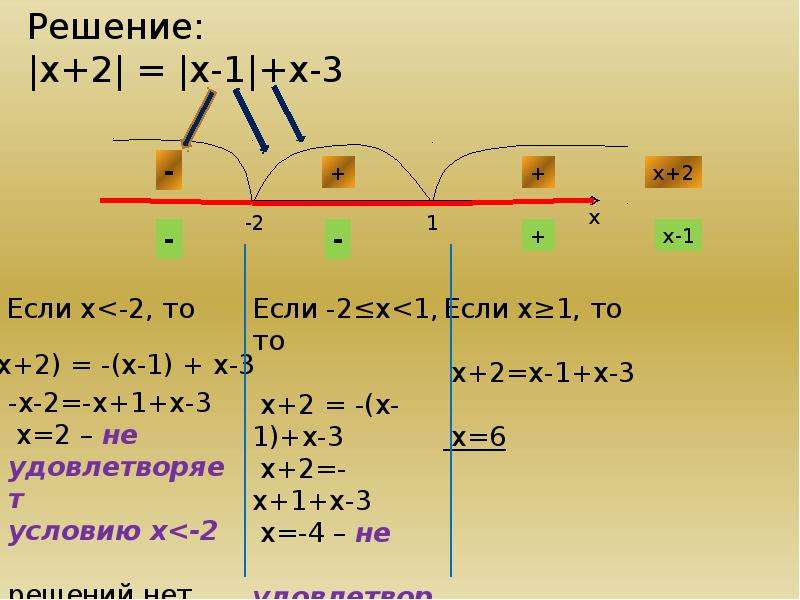
Не забывайте о знаках при решении уравнений с модулем: для положительных чисел модуль равен самому числу, а для отрицательных — противоположному.

В случае, если у вас сложное уравнение с несколькими модулями, используйте метод промежутков поэтапно для каждого модуля, а затем объединяйте результаты.
Решая уравнение с модулем, всегда проверяйте полученные решения в исходном уравнении, чтобы убедиться в их корректности.

Решение уравнений с модулем методом промежутков. Алгоритм решения.
После того как вы решите все промежутки, не забывайте о возможных исключениях, которые могут появиться из-за ограничений, накладываемых на переменные.

ЕНТ Решение уравнений с модулем, методом промежутков

Старайтесь работать с графиками функций модулей, чтобы лучше понять, как различные выражения могут изменяться в зависимости от значений переменных.

УРАВНЕНИЯ С МОДУЛЕМ Метод интервалов для решения уравнений

