Угловые характеристики параллелограмма: высоты и их взаимное расположение
На этой странице собраны полезные советы и примеры, как правильно вычислить угол между высотами, проведёнными из одной вершины параллелограмма. Знание этой геометрической особенности поможет в решении задач, связанных с углами, и улучшит понимание свойств параллелограмма.

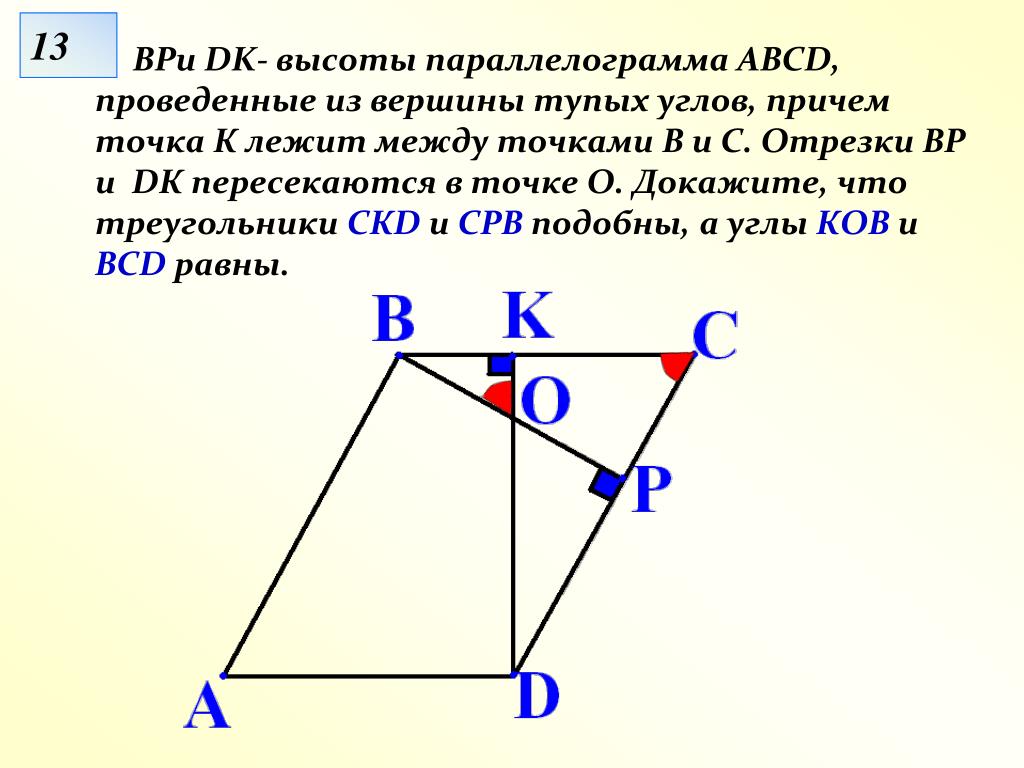

Для начала важно помнить, что угол между высотами параллелограмма можно найти, используя теорему о плоскости. Для этого нужно правильно определить взаимное расположение высот и определить их угол с помощью векторов.

Геометрия Докажите, что угол между высотами параллелограмма, проведенными из вершины тупого угла
Если у вас есть координаты вершин параллелограмма, то угол между высотами можно вычислить с использованием формулы скалярного произведения векторов. Для этого важно точно вычислить векторы, направленные вдоль высот.
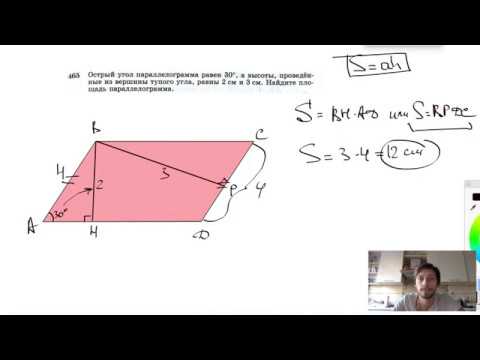
№465. Острый угол параллелограмма равен 30°, а высоты, проведенные из вершины тупого угла, равны

Обратите внимание, что угол между высотами всегда будет острым, если параллелограмм не является прямоугольным. Для прямоугольного параллелограмма угол между высотами будет равен 90 градусам.
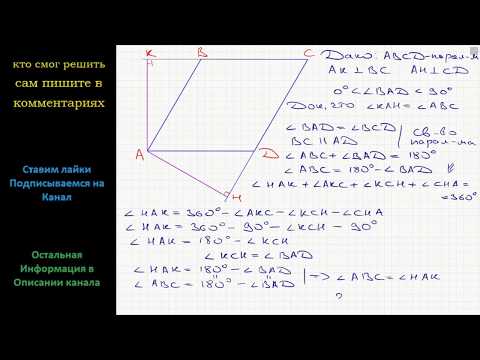
Геометрия Докажите, что угол между высотами параллелограмма, проведенными из вершины острого

Если параллелограмм является ромбом, то высоты, проведённые из одной вершины, будут располагаться под одинаковым углом. Это свойство можно использовать для упрощения расчётов углов.

Геометрия Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен 60

Используя свойства параллелограмма и его симметрии, можно найти угол между высотами, зная только длины сторон и высот. Это позволяет избежать сложных вычислений, связанных с углами.

Геометрия Угол между высотами параллелограмма, проведенными из вершины тупого угла, равен 30
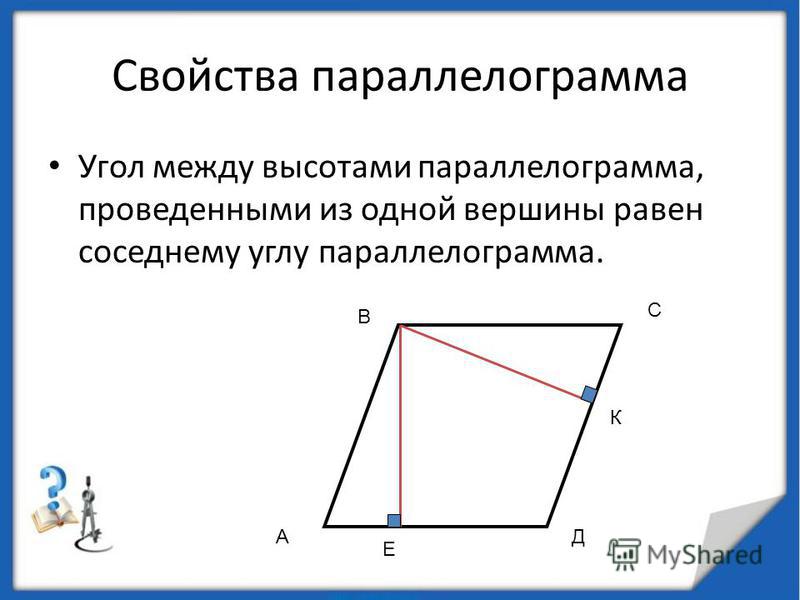
Не забывайте, что для вычисления угла между высотами также можно использовать тригонометрические функции, такие как синус и косинус, если известны длины высот и основания параллелограмма.

Как найти угол между прямой и плоскостью? СТЕРЕОМЕТРИЯ - TutorOnline

Иногда бывает полезно разложить задачу на несколько частей, например, вычислить угол между двумя прямыми, а затем использовать результат для нахождения угла между высотами.

Сингапурская головоломка Задача на логику

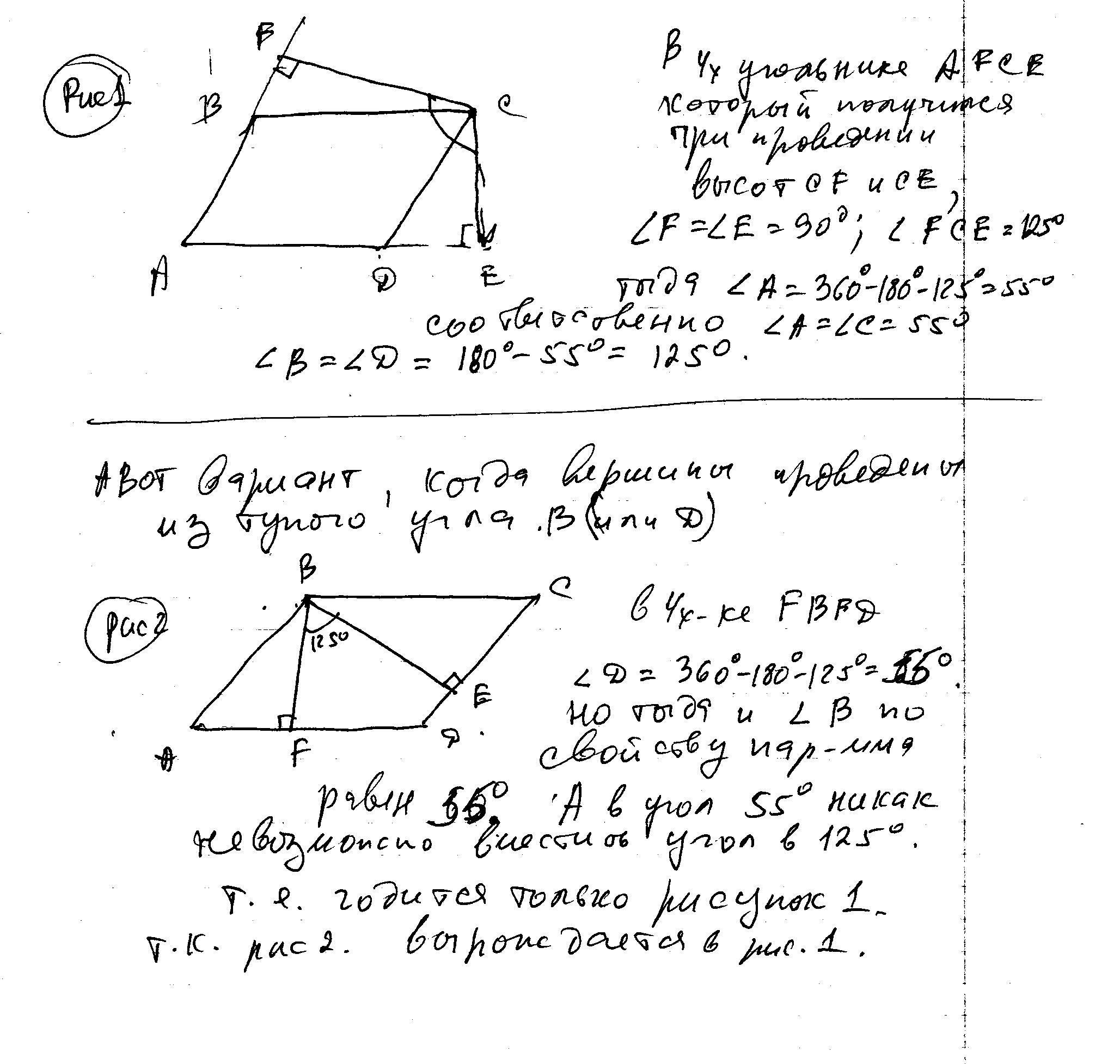
Помните, что угол между высотами можно найти как дополнительный угол к углу между соответствующими сторонами параллелограмма. Это важно для корректного применения формул углов в геометрии.
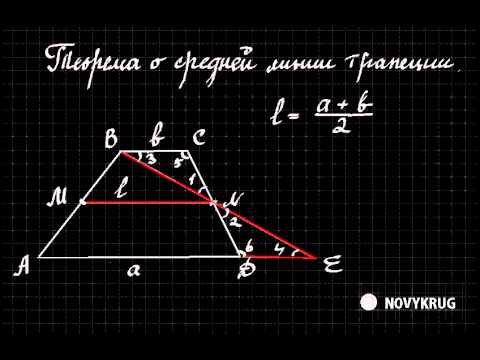
Теорема о средней линии трапеции

Для угла между высотами параллелограмма также можно использовать метод проекций, если вам известны углы между сторонами параллелограмма. Это позволяет сделать решение более наглядным.


Если параллелограмм является прямоугольным, угол между высотами всегда будет равен 90°. Однако для других типов параллелограммов угол будет зависеть от углов между его сторонами, что нужно учитывать при вычислениях.

Геометрия Найдите углы параллелограмма, если угол между его высотами, проведенными из одной вершины
