Решение геометрических задач с углами и их взаимными равенствами: подробный обзор
В данном разделе вы найдете полезные советы по использованию углов в геометрии, включая равенство углов и их взаимосвязь. Рассмотрим, как правильно применять эти знания при решении различных задач, а также ключевые принципы, которые помогут разобраться с углами 1, 2 и 3, где угол 3 равен 120 градусам.


При решении задач с углами важно помнить, что равенство углов может значительно упростить решение, особенно если один из углов известен.

Как найти угол. Я нашёл 120 градусов таким способом. How to find an angle of 120 degrees.
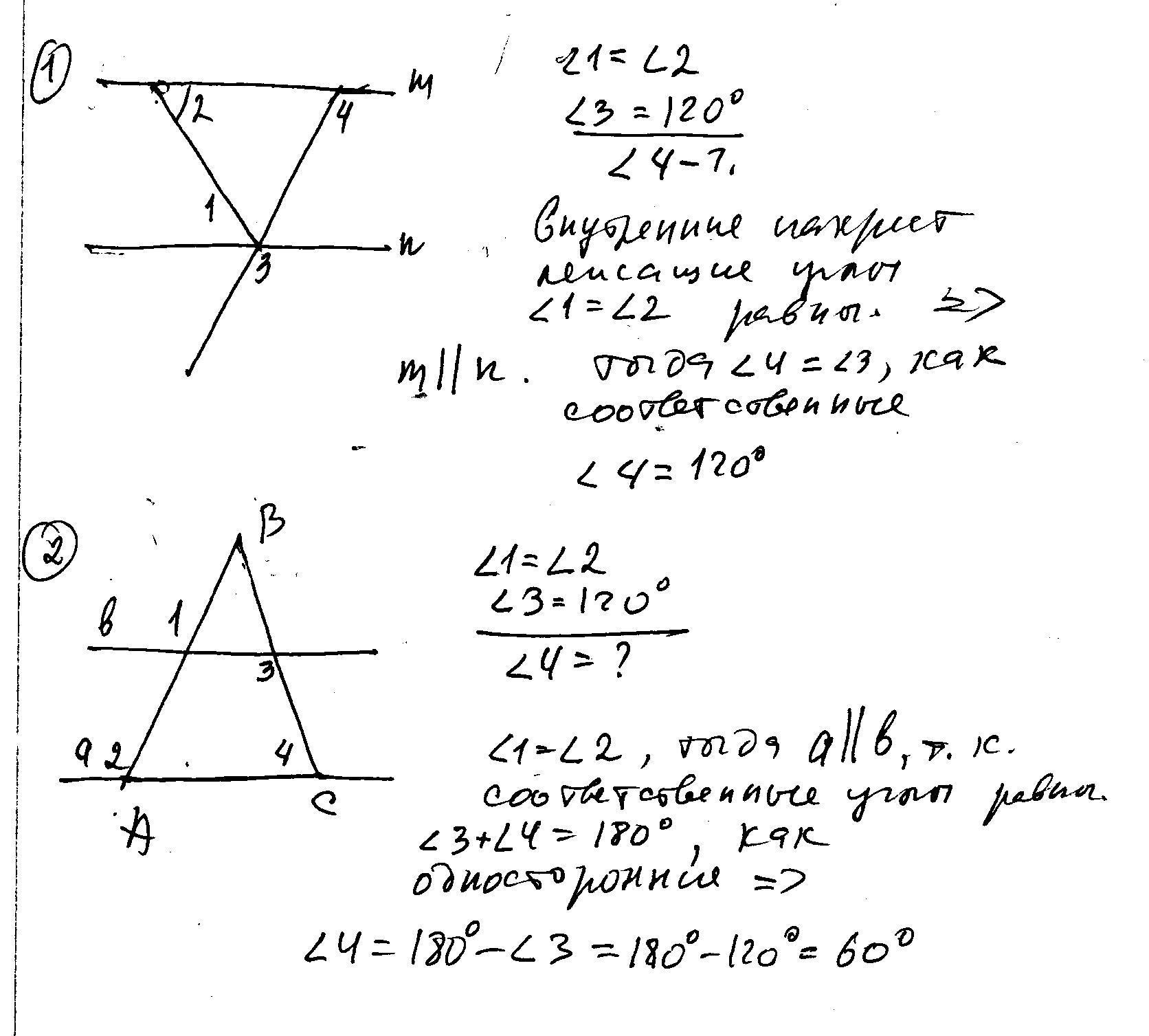
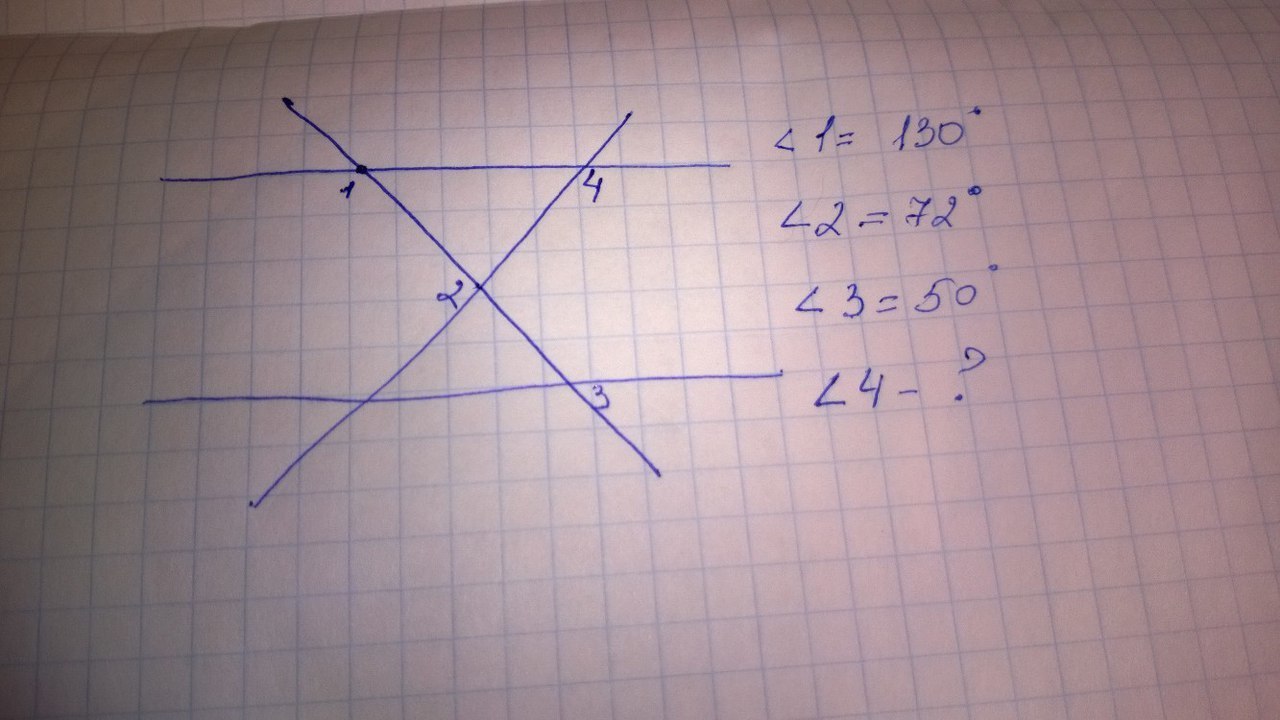
Для вычисления углов в многоугольниках воспользуйтесь формулой для суммы углов многоугольника, это поможет определить недостающие величины.

Чему равен угол между минутной и часовой стрелками?

Если два угла равны между собой, можно применить теорему о смежных углах, что ускорит решение задачи.

Построение угла 120 градусов с помощью циркуля и линейки.

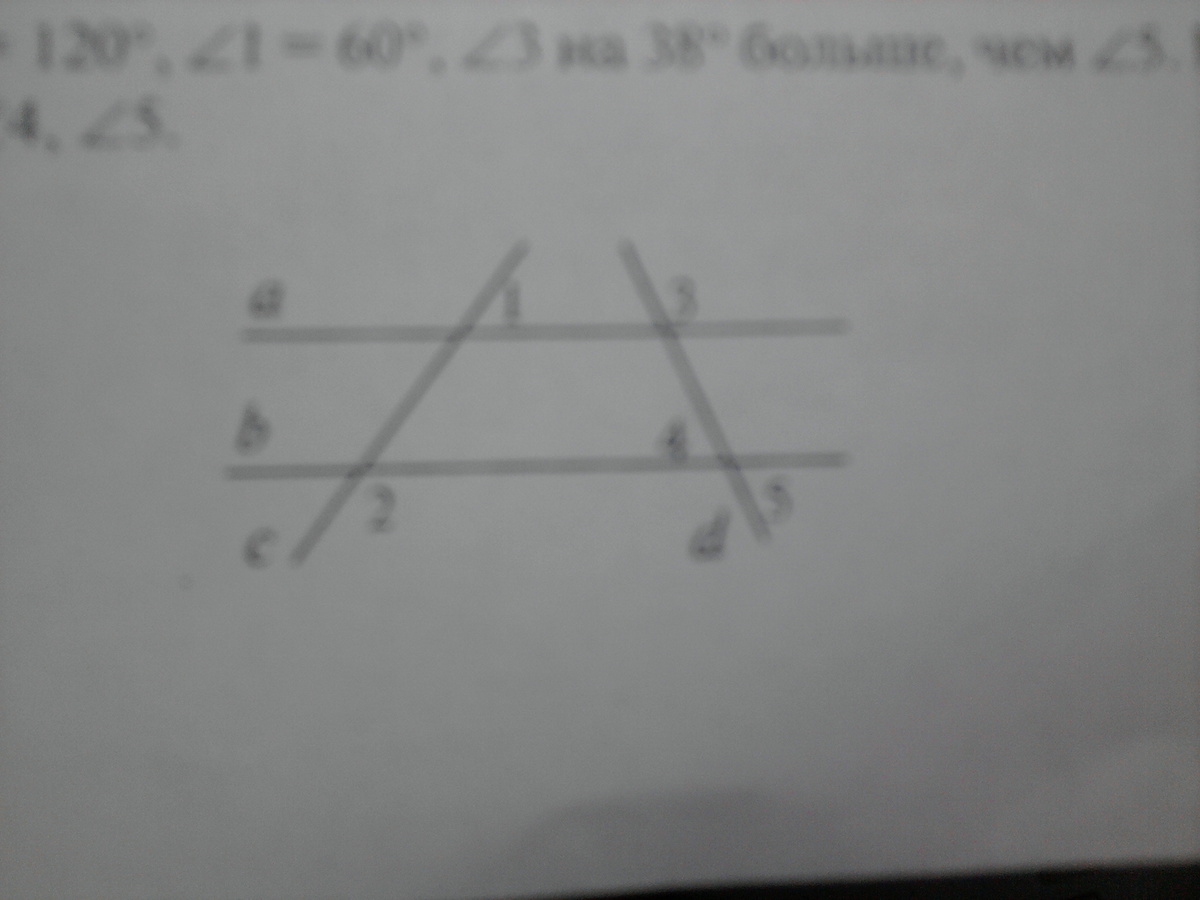
Углы, сумма которых составляет 180 градусов, являются смежными. Это важное свойство, которое можно использовать при решении задач с прямыми углами.
Смежные углы. 7 класс.

Если в задаче имеется угол 120 градусов, постарайтесь использовать его как часть большего угла или системы углов, чтобы легко вычислить недостающие значения.
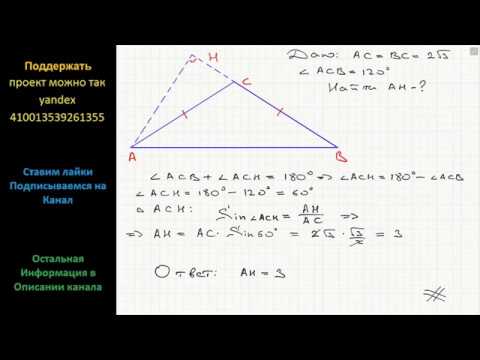
Геометрия В треугольнике ABC AC=BC=2(3)^(1/2), угол C равен 120. Найдите высоту AH
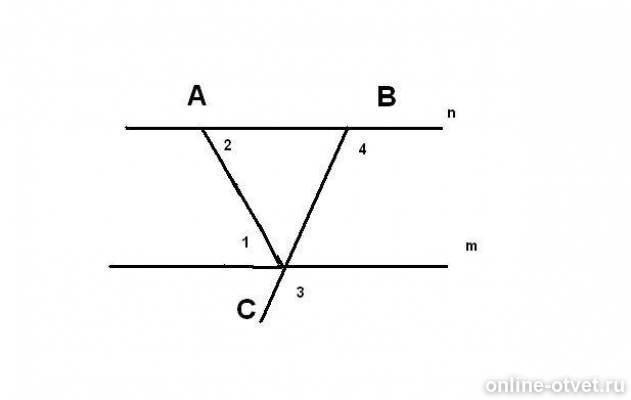
Обратите внимание на контекст задачи: углы 1 и 2 могут быть равными, если они являются внутренними углами параллельных прямых.

Угол 30 градусов без угломера
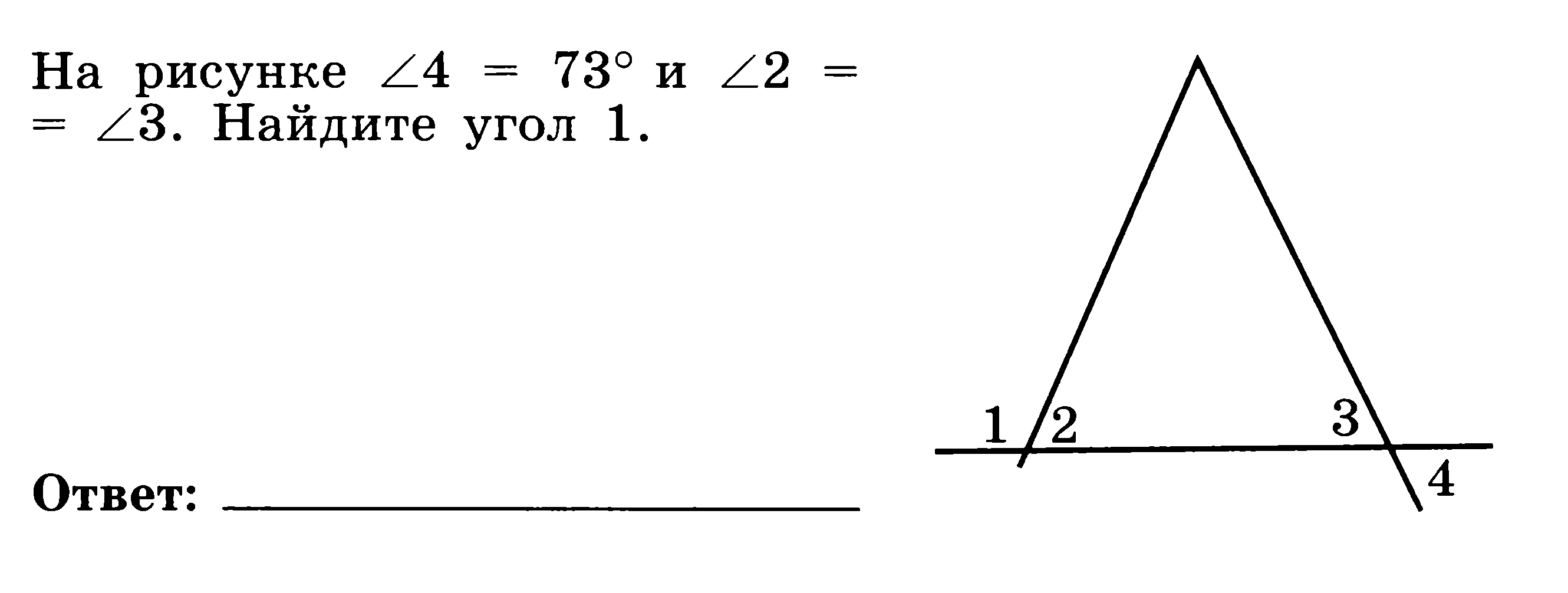

Для правильного понимания задач с углами важно визуализировать ситуацию, особенно если речь идет о многоугольниках или пересекающихся прямых.
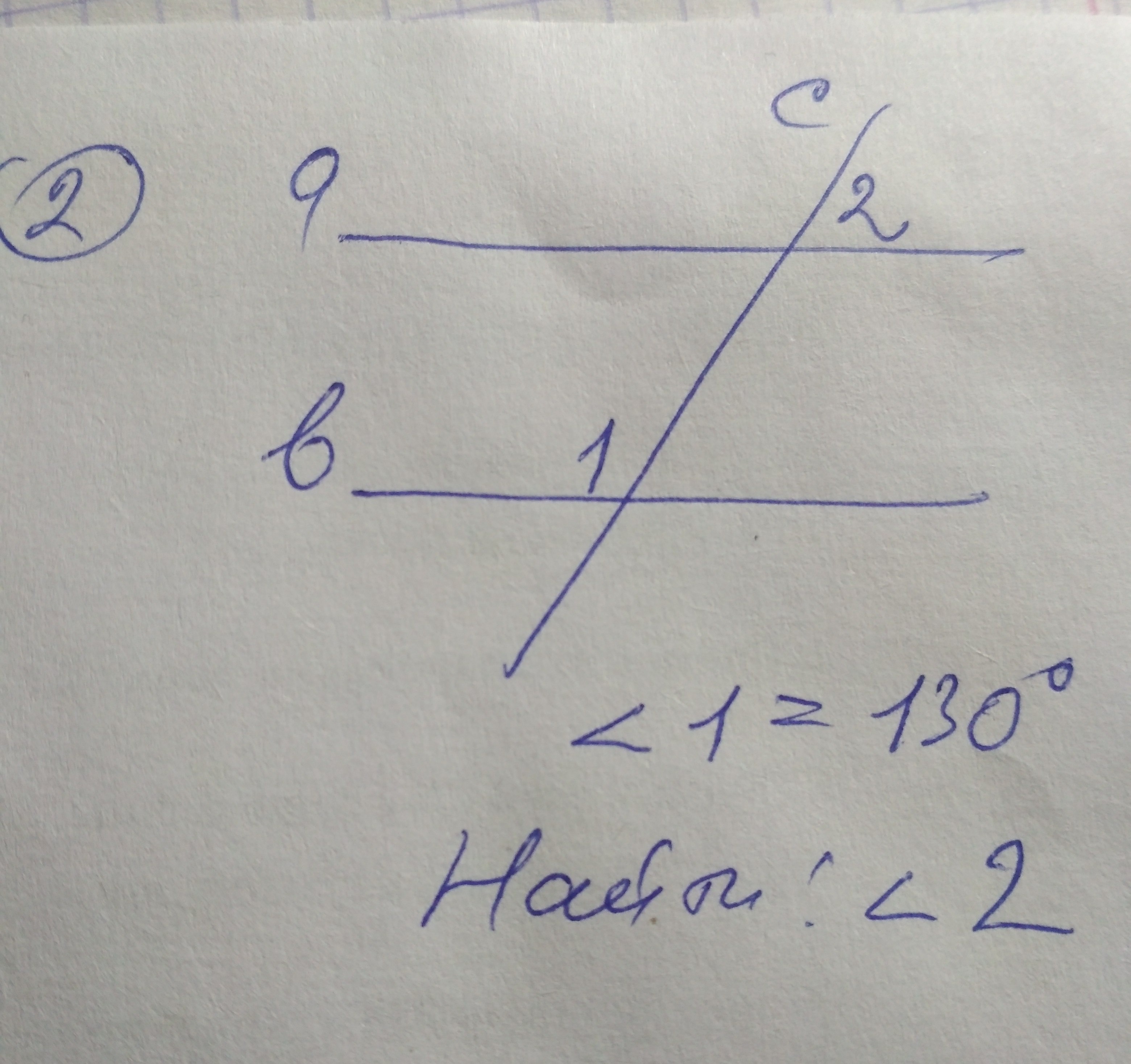
При использовании углов 120 градусов часто полезно помнить, что такие углы встречаются в равносторонних треугольниках и некоторых многоугольниках.

Вертикальные углы. 7 класс.

Классный способ для разметки любого угла без транспортира.
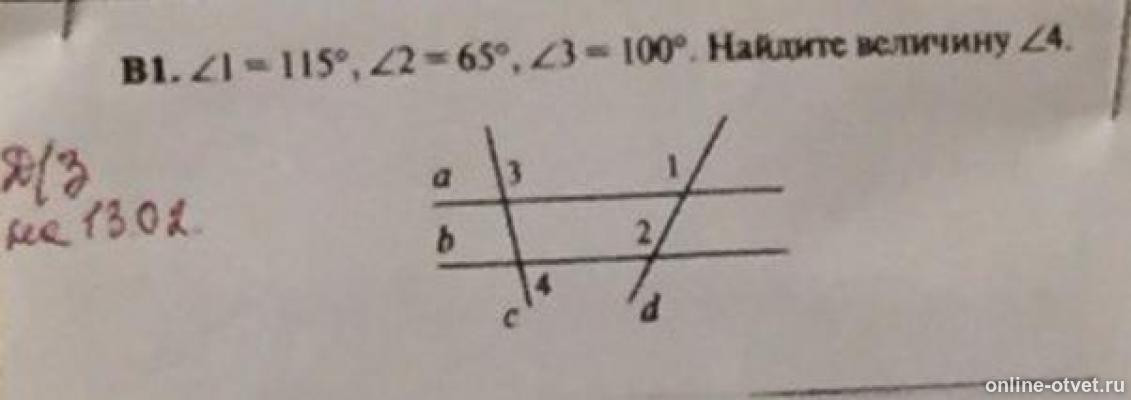
Если вам нужно решить задачу с углами на плоскости, всегда проверяйте, соблюдаются ли условия параллельности или перпендикулярности прямых.
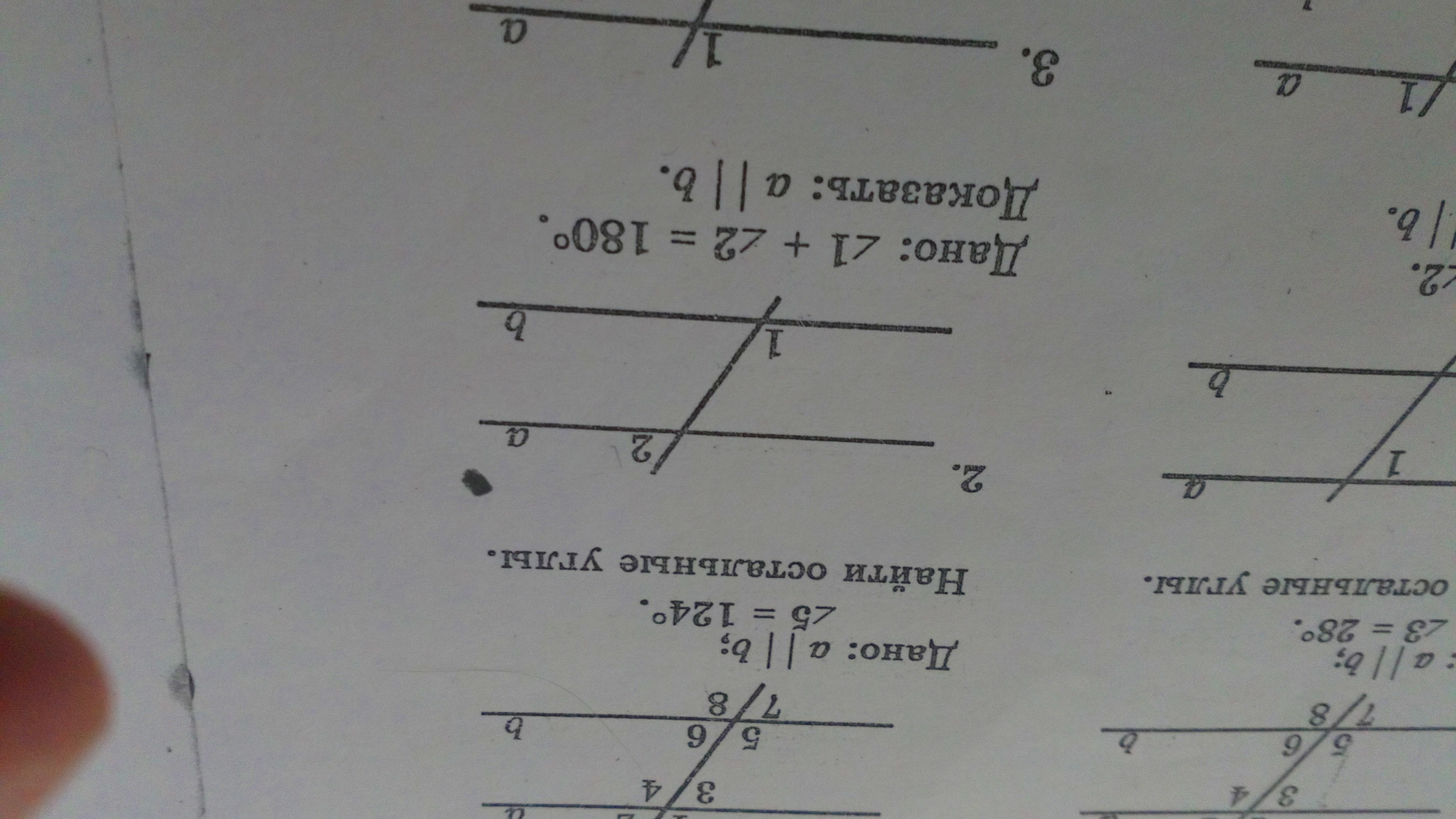
В задачах с углами важно уметь использовать теоремы о внешних и внутренних углах для упрощения расчетов и нахождения необходимых значений.

7 класс, 11 урок, Смежные и вертикальные углы