Как медианы треугольника встречаются в одной точке и что это значит
Медианы треугольника — это линии, соединяющие вершины треугольника с серединами противоположных сторон. Все три медианы пересекаются в одной точке, которая называется центроидом. Эта точка имеет интересные геометрические свойства и важное применение в различных областях математики.
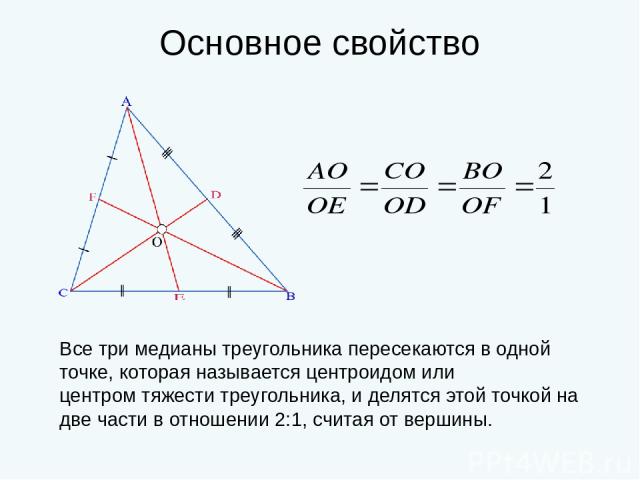
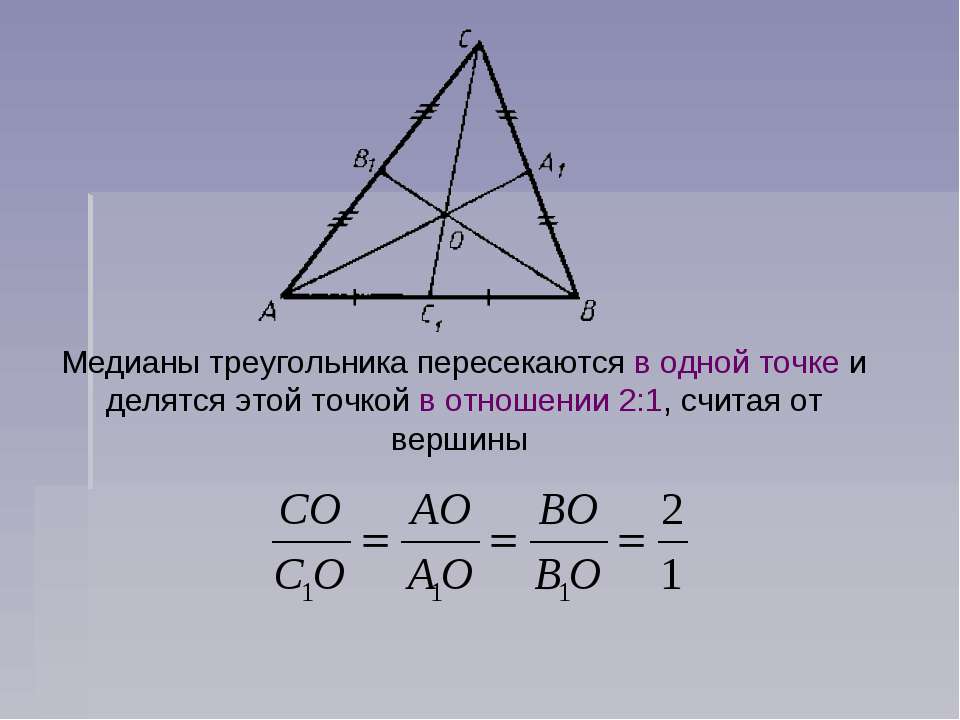
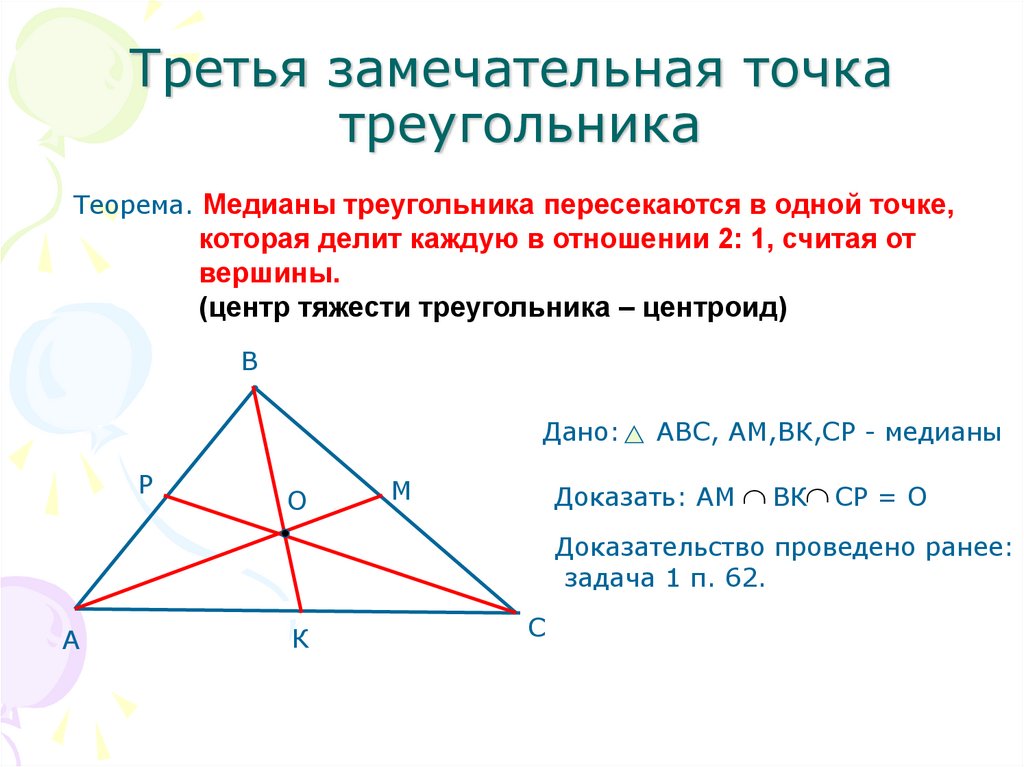
Для лучшего понимания, представьте себе треугольник, нарисованный на бумаге, и попробуйте провести медианы вручную, чтобы увидеть, как они пересекаются в одной точке.

Теорема о точке пересечения медиан треугольника. Доказательство. 8 класс.

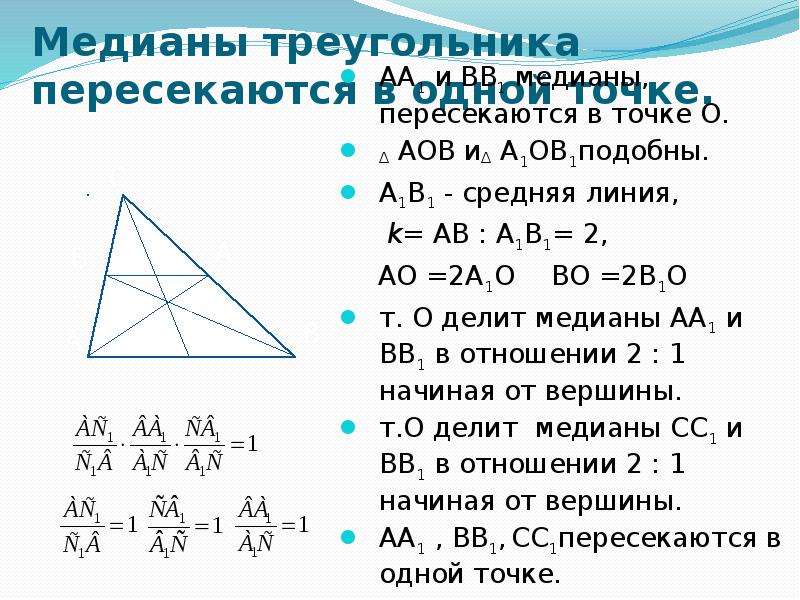
Когда медианы треугольника пересекаются, эта точка делит каждую медиану в отношении 2:1, считая от вершины до середины стороны.
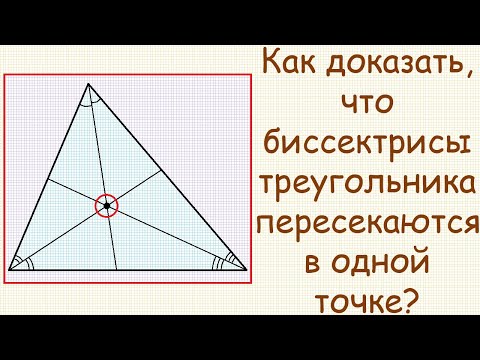
Как доказать, что биссектрисы треугольника пересекаются в одной точке?
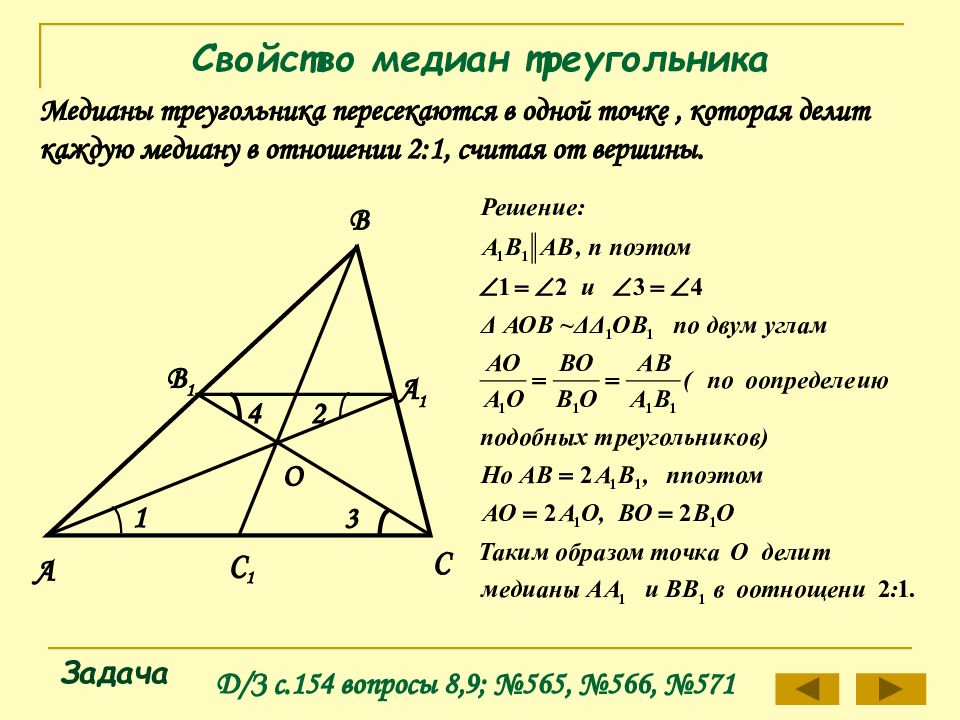
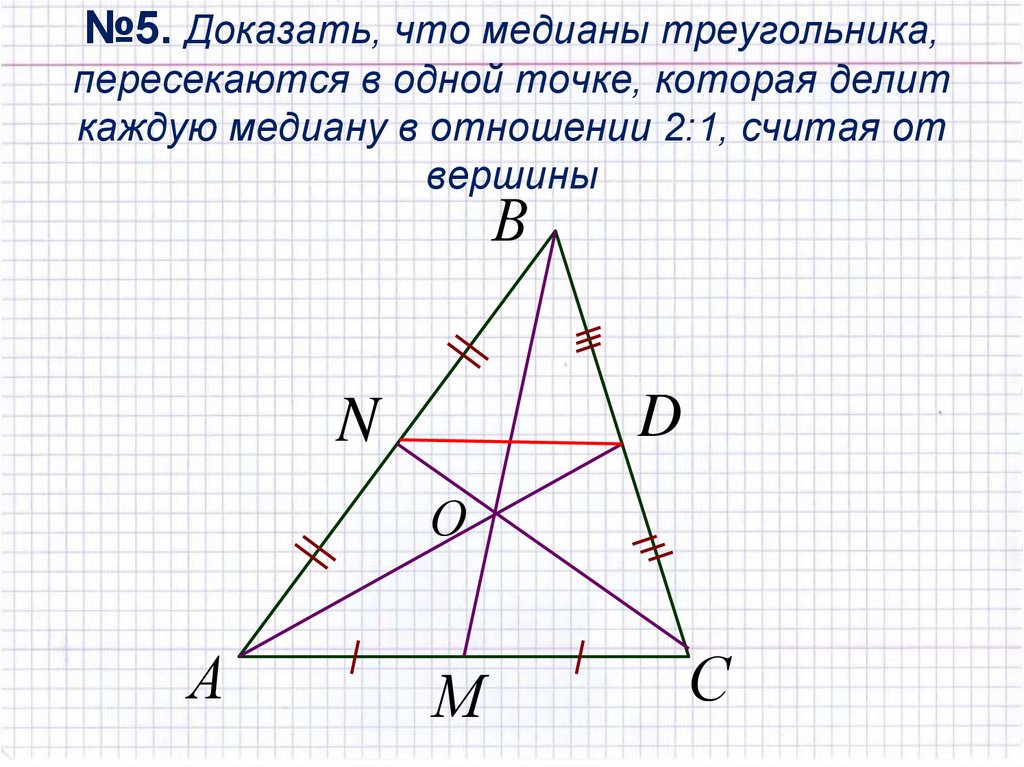
Понимание расположения медиан помогает решать задачи, связанные с нахождением центроидов треугольников в различных контекстах, например, в задачах на равновесие или распределение массы.

ГЕОМЕТРИЯ 8 класс. Свойство медиан треугольника
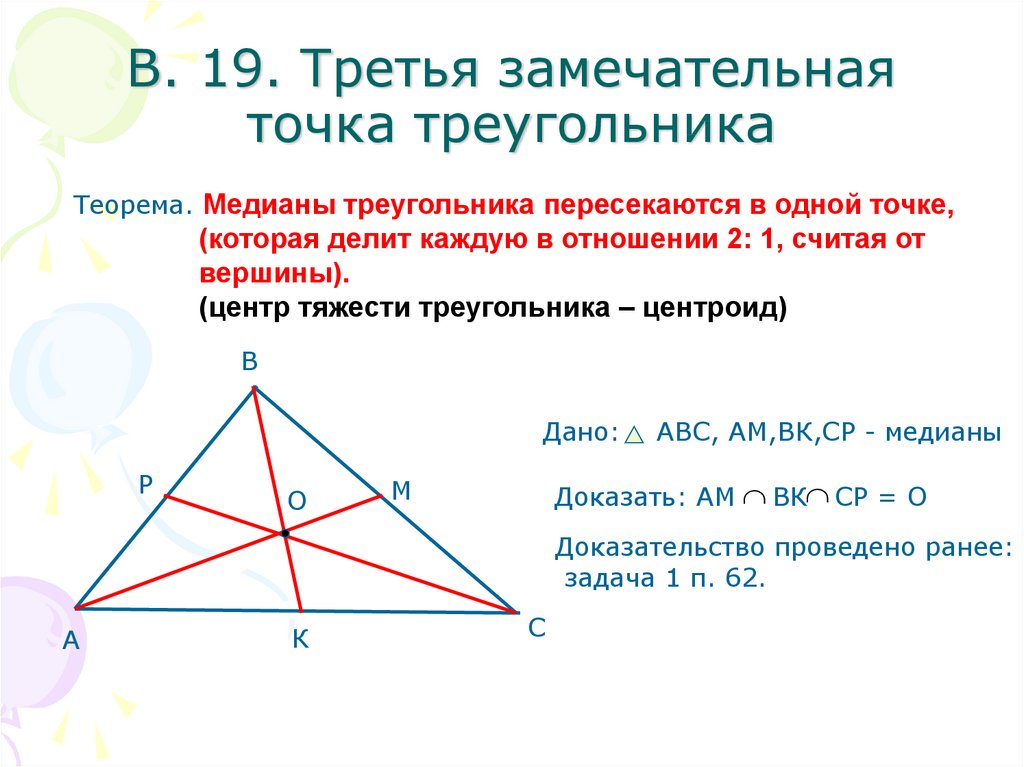
Важно помнить, что центроид является не только геометрической, но и физической точкой равновесия треугольника, если представить его как тонкую однородную пластину.
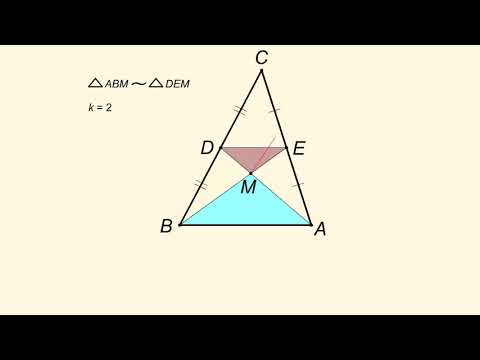
Точка пересечения медиан в треугольнике
Для вычислений, связанных с центроидом, полезно использовать формулы для координат центроида, если вам известны координаты вершин треугольника.
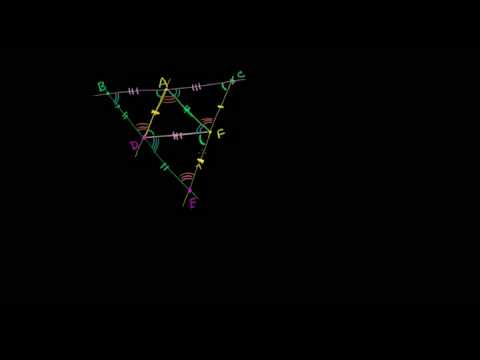
Высоты треугольника пересекаются в одной точке
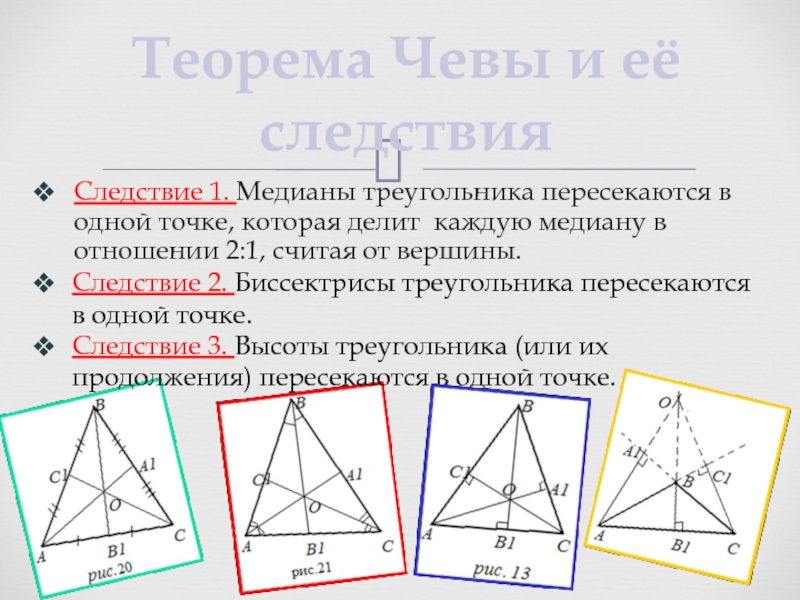
При изучении медиан треугольника полезно также рассмотреть их взаимное расположение и понять, как они делят фигуру на более простые геометрические части.

Медианы треугольника пересекаются в точке . Найдите длину медианы
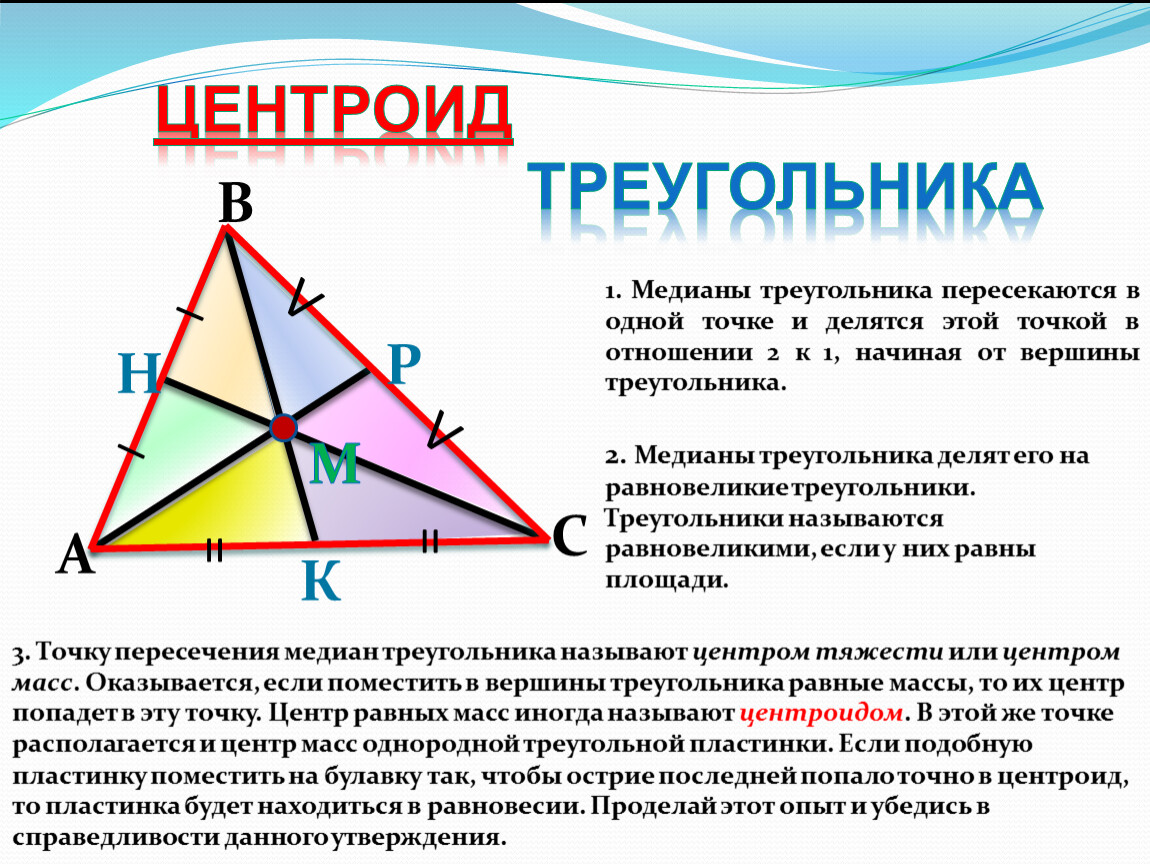
Визуализация медиан и их пересечений помогает не только понять теоретическую концепцию, но и улучшить навыки работы с геометрическими фигурами в целом.
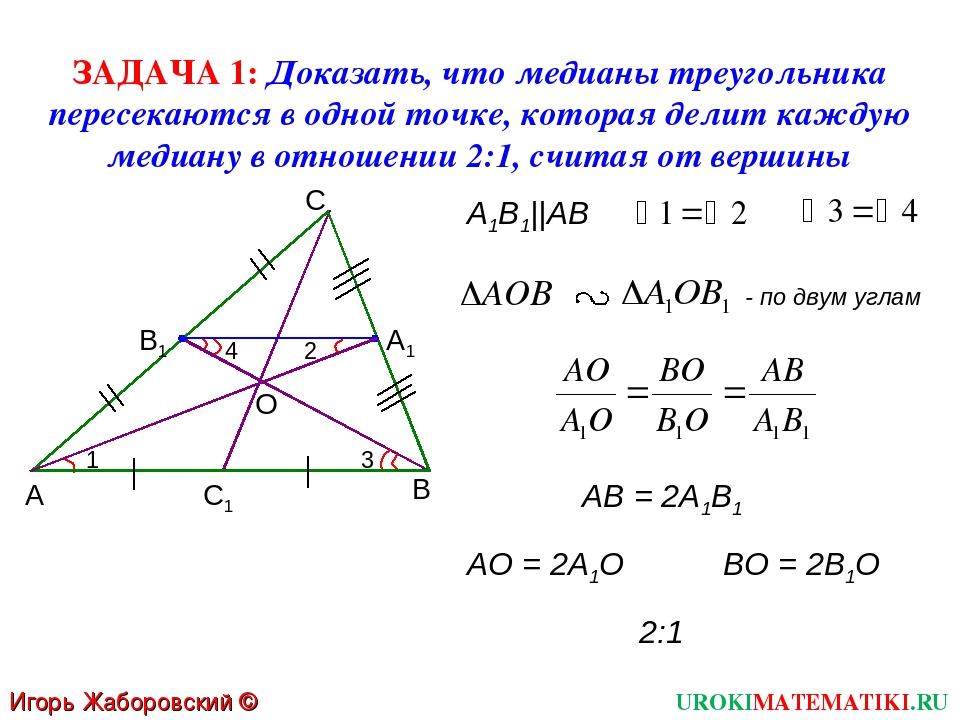
Чтобы лучше запомнить свойство медиан, можно создать несколько различных треугольников и исследовать их медианы с помощью линейки и угольника.

Длина медианы треугольника
Почему медианы пересекаются в одной точке? - Математика для поступающих в ВУЗ по ЕГЭ - 21-07-2021

Помимо вычислений, изучение медиан треугольника развивает пространственное воображение и способность анализировать геометрические формы.
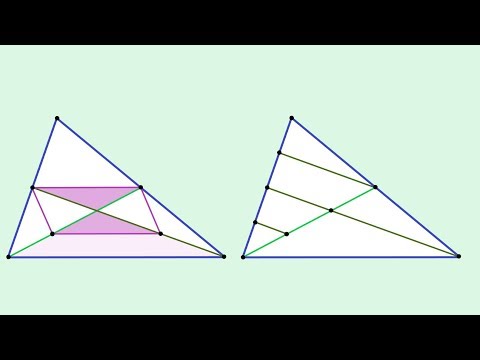
22 Медианы треугольника пересекаются в одной точке
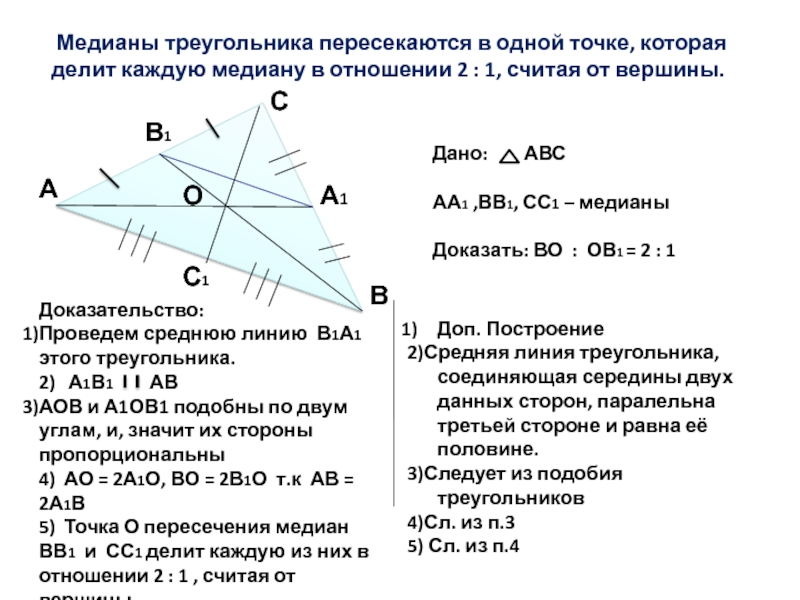
Понимание свойств медиан также поможет вам разобраться в более сложных темах, таких как теорема о центре масс в физике или аналитическая геометрия.

Точка пересечения медиан.