Как представить комплексное число в различных формах и выбрать оптимальную

Комплексные числа могут быть представлены в нескольких формах, каждая из которых имеет свое специфическое применение. В этой подборке мы рассмотрим три основные формы комплексных чисел: алгебраическую, тригонометрическую и экспоненциальную. Также предложим полезные советы по их использованию в различных задачах и расчетах.

При решении уравнений с комплексными числами удобно использовать алгебраическую форму, так как она позволяет напрямую оперировать с действительными и мнимыми частями.

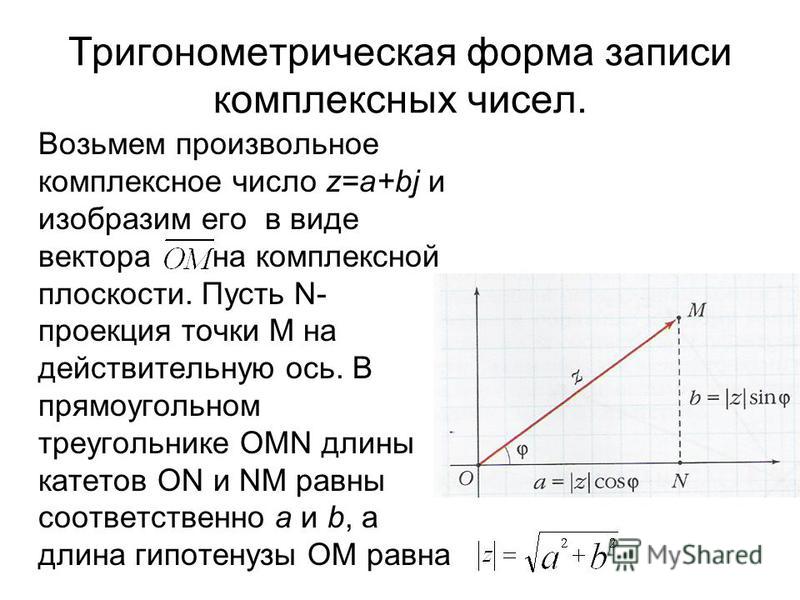
Тригонометрическая форма особенно полезна при умножении и делении комплексных чисел, поскольку упрощает вычисления с углами и модулями.

Экспоненциальная форма комплексного числа наилучшим образом подходит для возведения чисел в степень и работы с корнями комплексных чисел.

Для упрощения преобразования комплексных чисел между разными формами используйте формулы Эйлера, которые связывают тригонометрическую и экспоненциальную формы.

Помните, что мнимая единица i определяется как корень из -1, и ее использование в расчетах всегда связано с извлечением квадратных корней из отрицательных чисел.

Алгебраическая форма подходит для наглядного представления комплексных чисел, особенно если необходимо выделить их действительную и мнимую части.

Использование тригонометрической формы особенно удобно при работе с аргументами и модулями комплексных чисел, так как она позволяет быстро вычислять их произведение и частное.

Если вам нужно выполнить возведение комплексного числа в степень, воспользуйтесь экспоненциальной формой, так как это значительно упростит вычисления.

Для вычислений с комплексными числами важно учитывать их геометрическую интерпретацию в комплексной плоскости, где каждая форма имеет свое визуальное представление.

Не забывайте, что каждая форма комплексного числа может быть полезна в зависимости от задачи, поэтому важно понимать, когда лучше применять ту или иную форму для упрощения расчетов.