Треугольники и теорема Фалеса: ключ к решению геометрических задач
На этой странице вы найдете полезные советы и примеры применения теоремы Фалеса для решения геометрических задач, связанных с треугольниками. Узнайте, как эта теорема помогает анализировать подобие треугольников и вычислять различные их характеристики.


Для правильного применения теоремы Фалеса важно точно определить пересекающиеся прямые и параллельность сторон.
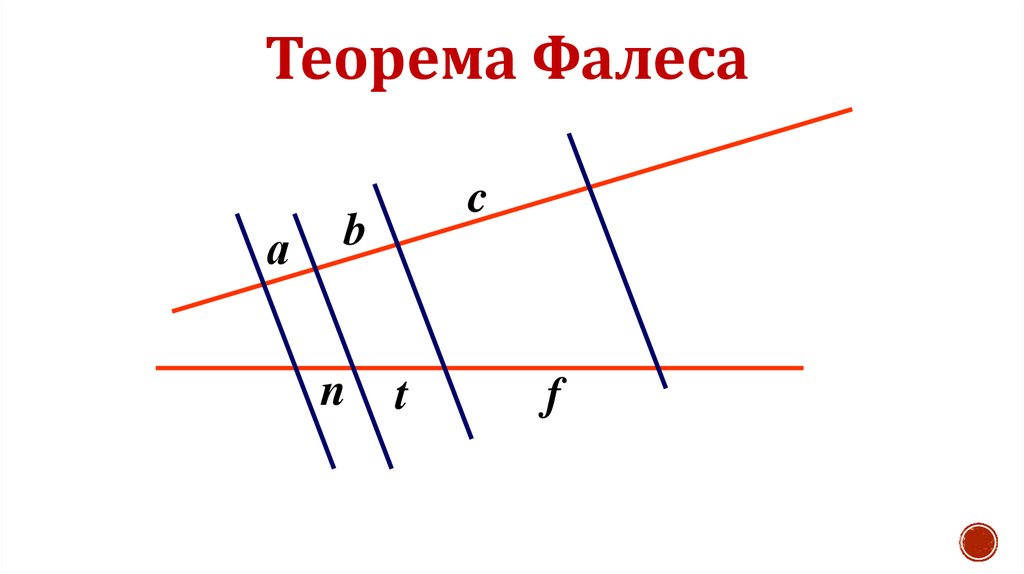
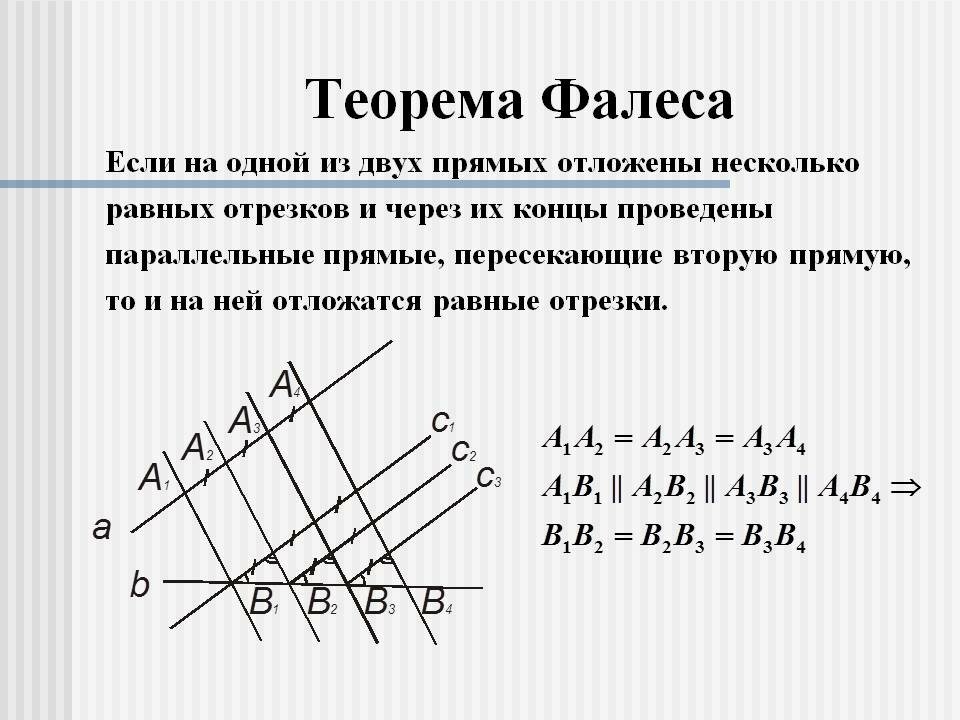
Теорема Фалеса

Проверяйте, чтобы отрезки, разделенные прямыми, имели пропорциональные длины, это ключевая особенность теоремы.

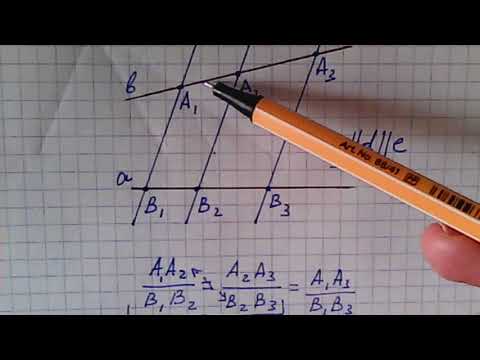
Геометрия 8 класс : Теорема Фалеса
Для вычислений используйте соотношение длин соответствующих сторон треугольников, полученных по теореме Фалеса.

ТЕОРЕМА ФАЛЕСА доказательство 384 Атанасян 8 класс

Применяйте теорему Фалеса не только для прямых, но и для анализа различных геометрических фигур, если они подходят по условиям.

Теорема Фалеса. Теорема о пропорциональных отрезках. Экстра Математика ЕГЭ

При решении задач, связанных с теоремой Фалеса, всегда сначала проверяйте, что стороны треугольников находятся в правильном соотношении.

Теорема Фалеса. 8 класс.
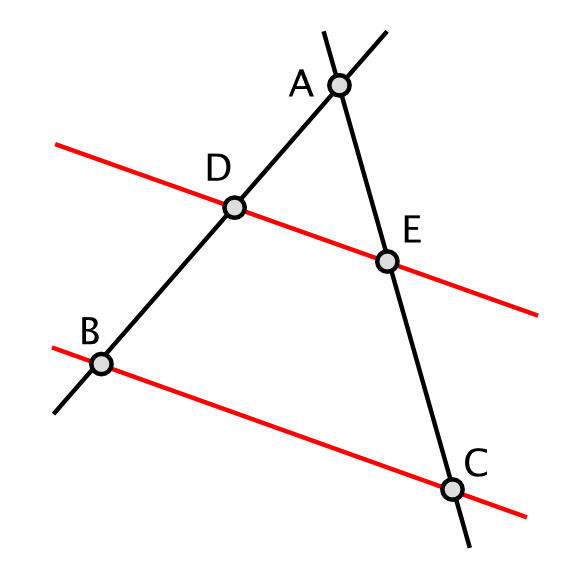
Используйте теорему Фалеса для построения подобных треугольников, что поможет лучше понять свойства фигуры.
Не забывайте о возможности применения теоремы Фалеса в обратном направлении — это может дать дополнительные способы решения задач.
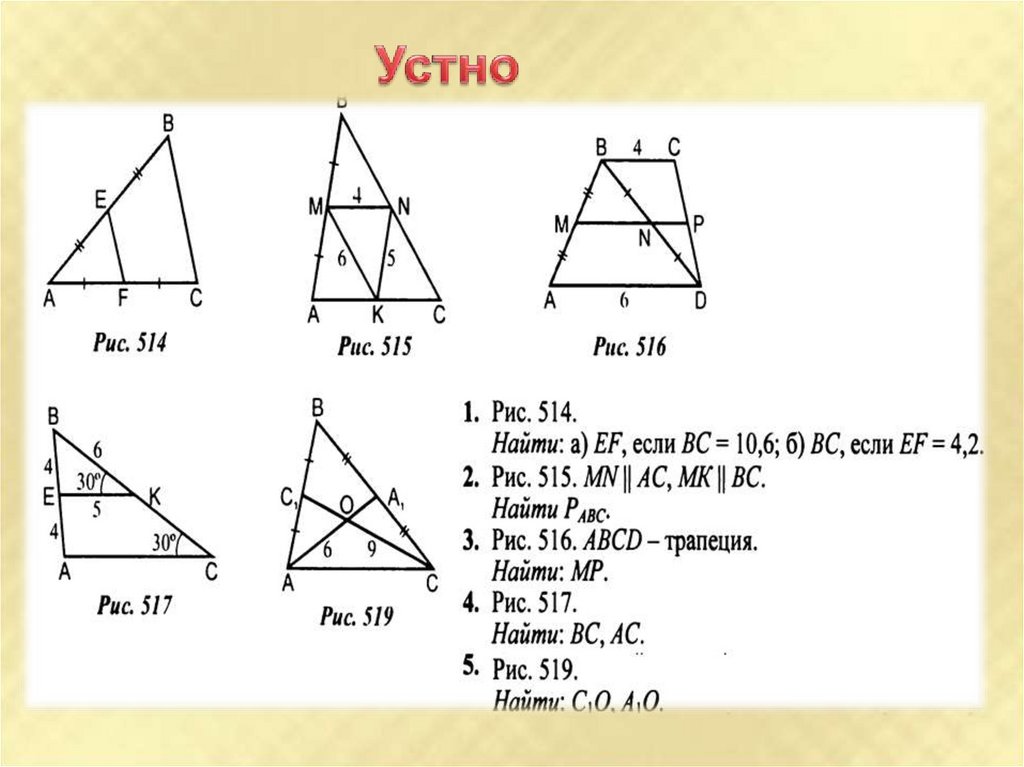
Запоминайте, что теорема Фалеса работает только в случае, если одна из прямых делит стороны треугольника пропорционально.

Для упрощения решения задач по теореме Фалеса пользуйтесь графическими методами или программами для черчения.

Будьте внимательны при определении условий задачи: теорема Фалеса применима только к подобным треугольникам, разделенным параллельными прямыми.