Тетраэдр, его структура и роль граней и вершин в геометрии

Тетраэдр является одной из основных геометрических фигур, изучаемых в математике и геометрии. Его структура, состоящая из четырех треугольных граней, имеет удивительные свойства, которые влияют на симметрию и другие характеристики фигуры. Здесь мы расскажем о ключевых моментах, связанных с этим объектом и предложим полезные советы для работы с тетраэдром.

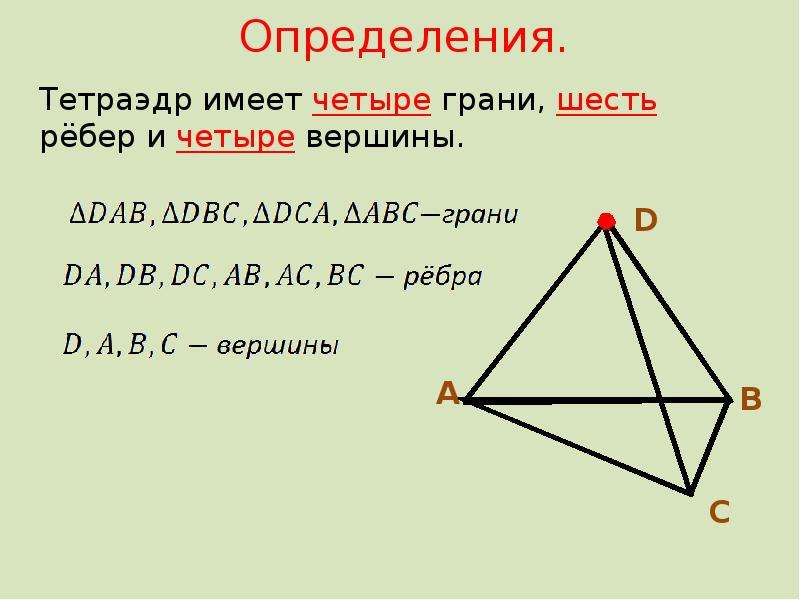
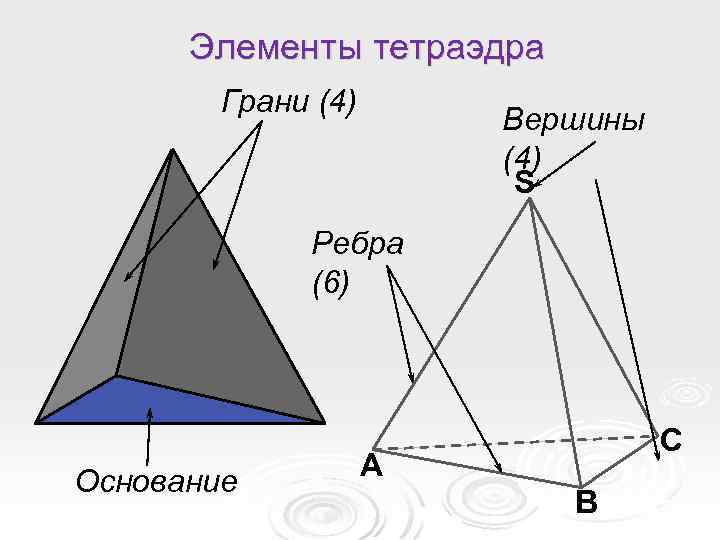
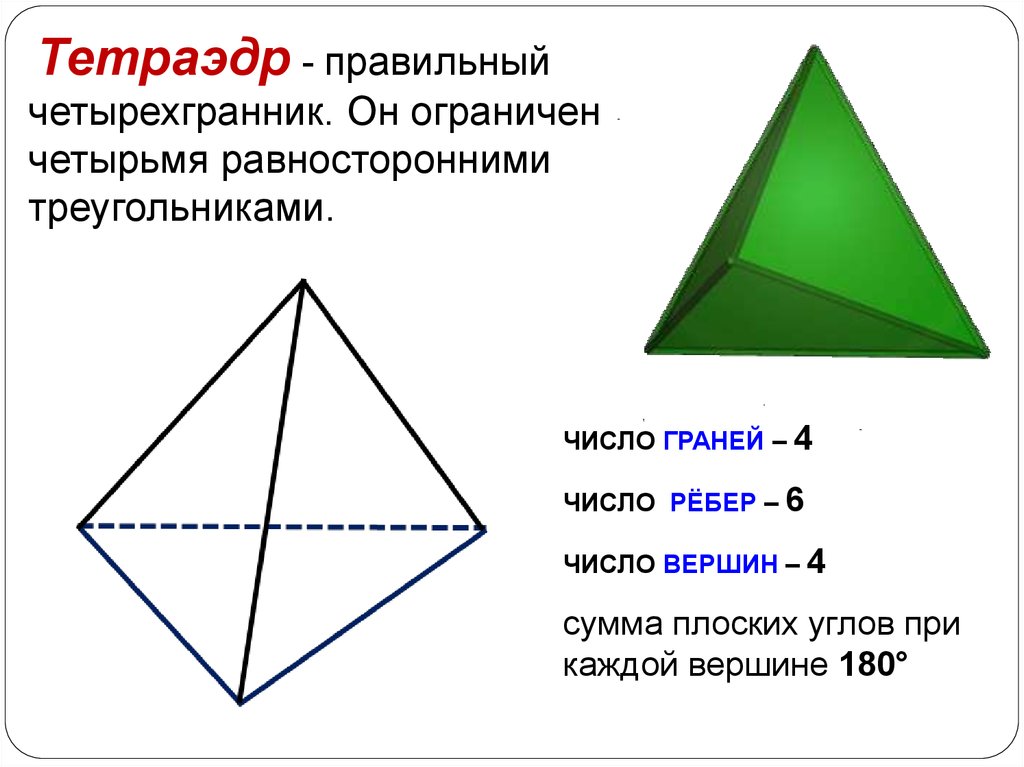
При изучении тетраэдра важно понимать, как его вершины и грани взаимодействуют между собой, создавая уникальную симметрию и форму.

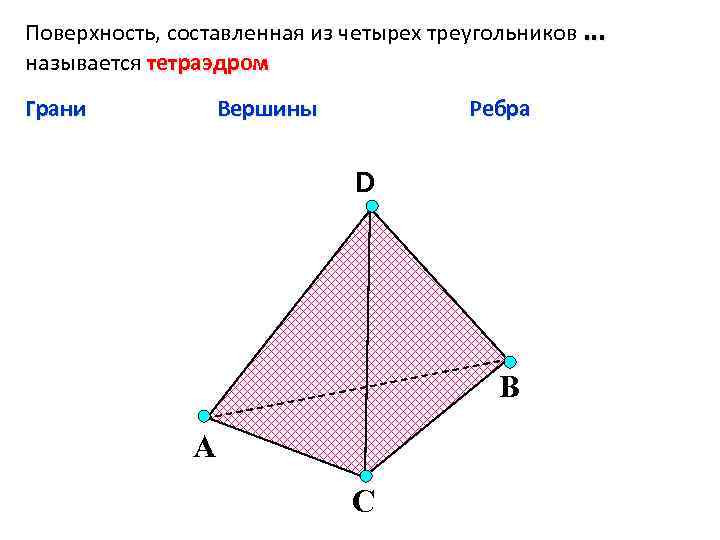
Чтобы лучше понять тетраэдр, попробуйте построить его с использованием различных материалов, таких как бумага или картон — это поможет вам наглядно увидеть его структуру.

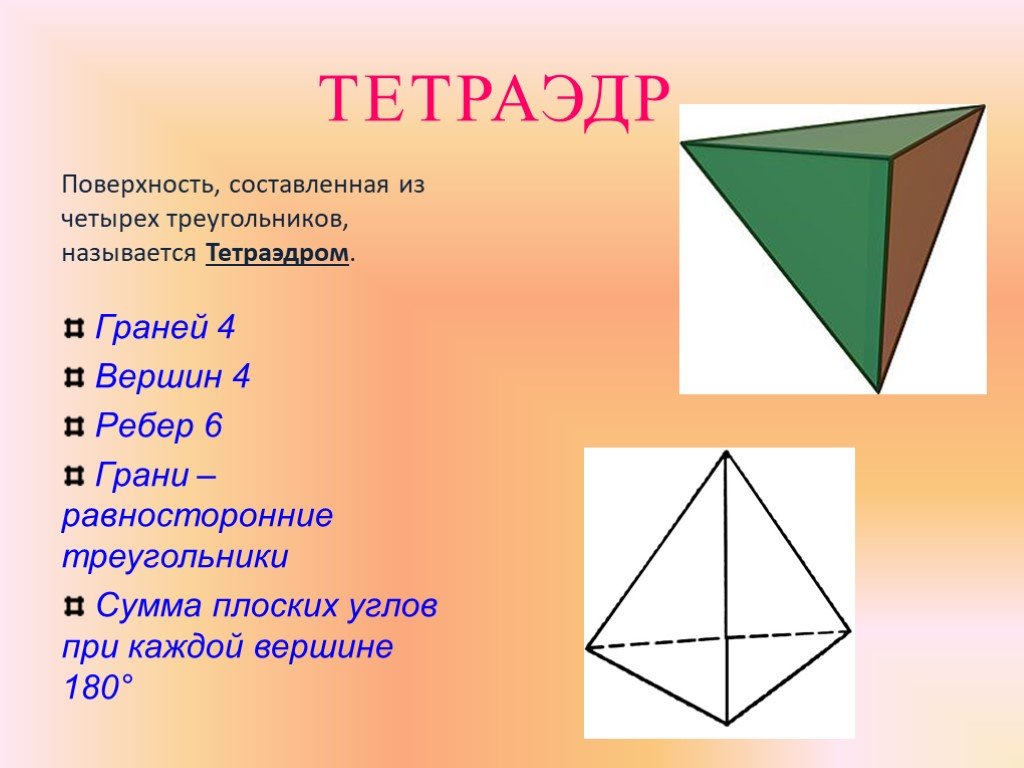
Не забывайте о том, что все грани тетраэдра — это равносторонние треугольники, что придает ему устойчивую симметричную форму.

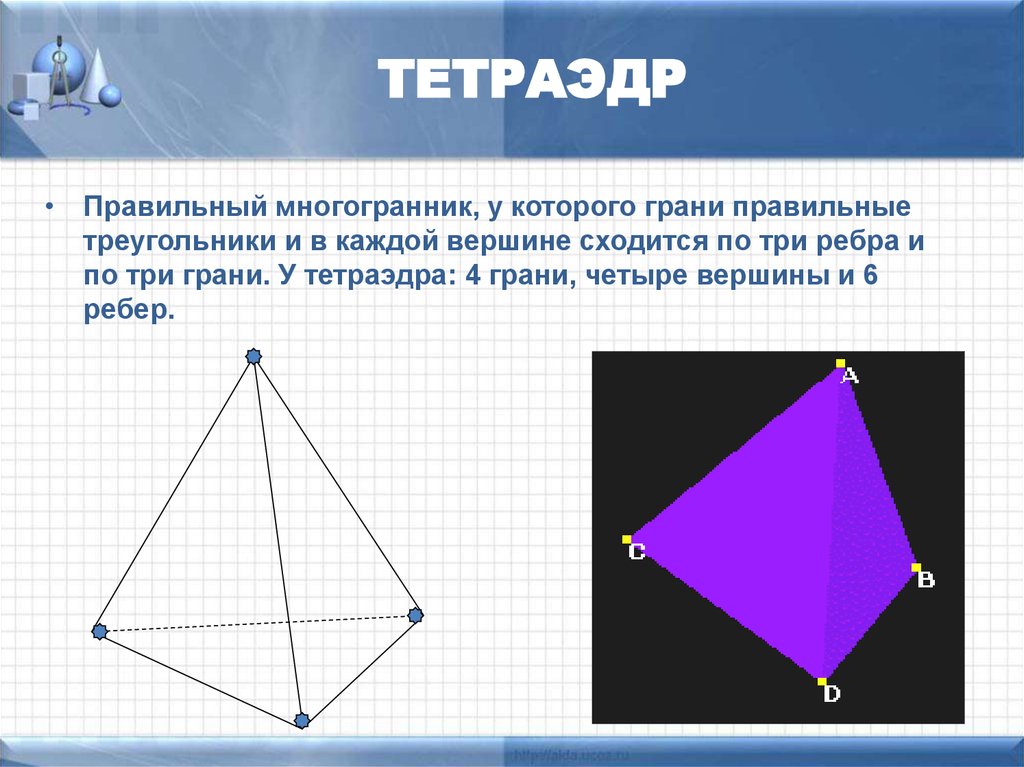
Для более глубокого анализа тетраэдра изучите его свойства в контексте теории групп, так как его симметрии могут быть описаны с помощью группы вращений.

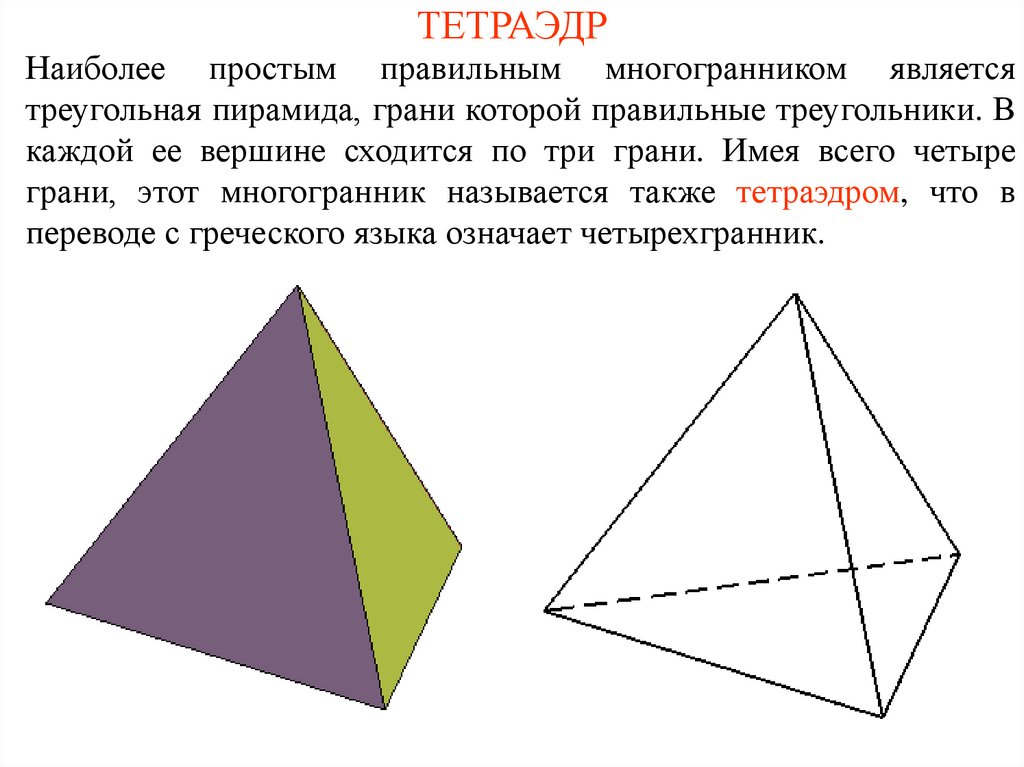
При работе с тетраэдром важно учитывать, как изменение углов между его гранями влияет на его геометрические и топологические свойства.

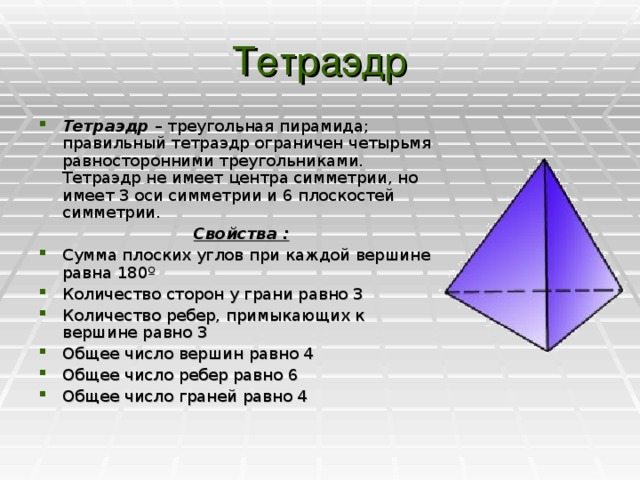
Используйте модели тетраэдра в 3D-графике или программировании, чтобы проиллюстрировать, как его грани и вершины меняются при различных трансформациях.

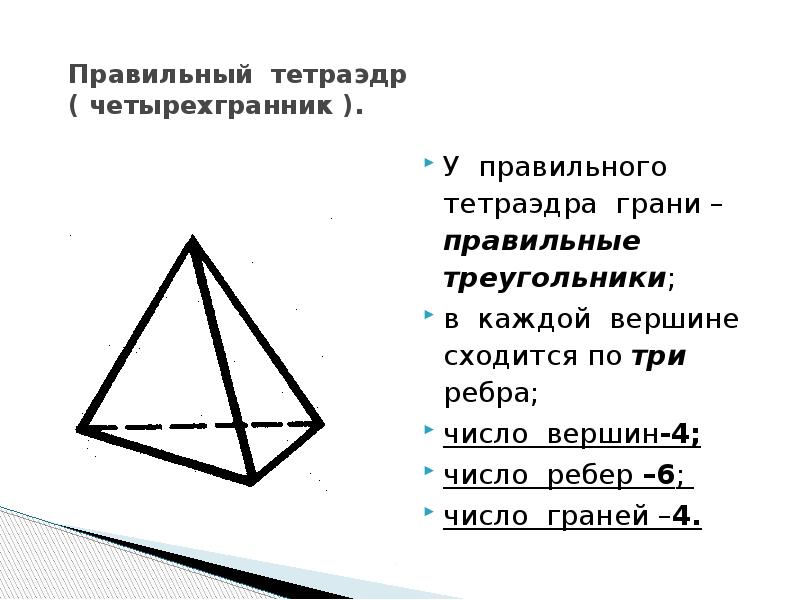
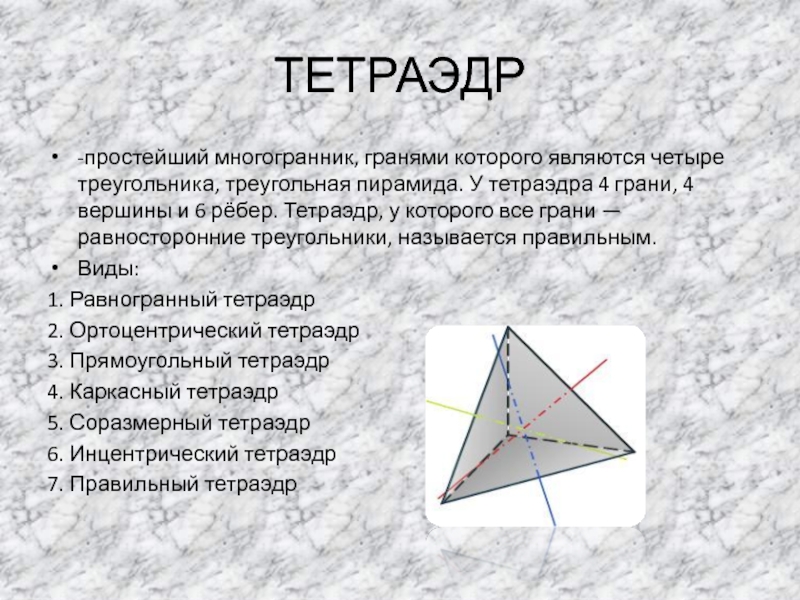
Если вы хотите изучить тетраэдр в контексте реальных приложений, посмотрите, как эта фигура используется в кристаллографии и молекулярной биологии.

При вычислениях с тетраэдром полезно знать формулы для объема и площади поверхности, что позволит вам быстрее решать задачи.

Обратите внимание, что тетраэдр может быть как правильным, так и неправильным, в зависимости от пропорций его граней и углов.

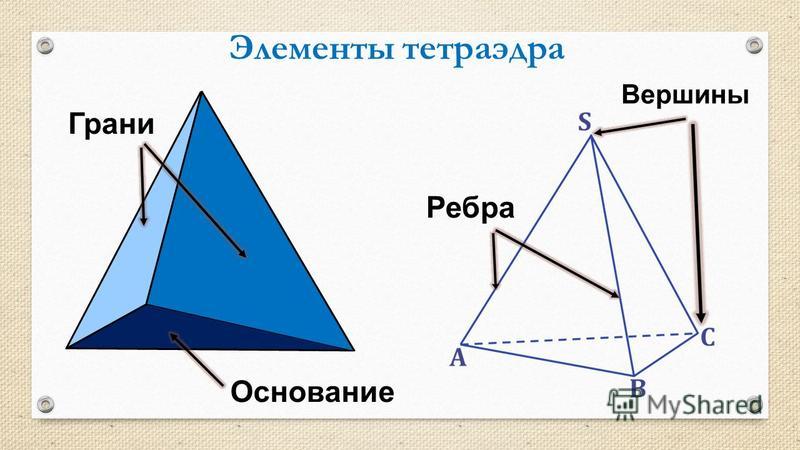
Для лучшего восприятия тетраэдра используйте графические программы или модели для визуализации его трехмерной структуры.