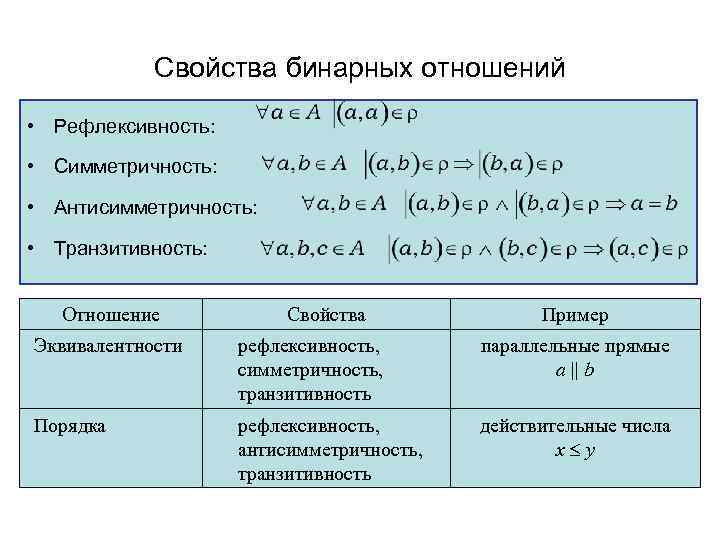
Свойство рефлексивности: ключевые аспекты и применение в математике
Рефлексивность — одно из базовых свойств бинарных отношений в математике. На этой странице вы найдете объяснения, примеры и полезные советы для глубокого понимания этой темы.



Всегда начинайте изучение рефлексивности с определения: оно предполагает, что каждый элемент множества относится сам к себе.

Интуитивная топология - теоретико множественные вопр. - бинарные отношения - свойства


Рассматривайте примеры из жизни, чтобы лучше понять рефлексивность, например, свойство равенства: любое число равно самому себе.

Проверяем свойства отношений

Рисуйте графы для визуализации: в рефлексивном отношении каждый узел будет иметь петлю.

Яворская Т.Л. - Понятийный аппарат математики - 5. Специальные свойства отношений


Практикуйтесь с задачами на проверку рефлексивности отношений в различных множествах.
9 Бинарные отношения - Роман Попков - ИТМО

Ищите контрпримеры, чтобы убедиться, что вы правильно понимаете, что не является рефлексивным.

Какие есть свойства математических операций и отношений? Душкин объяснит
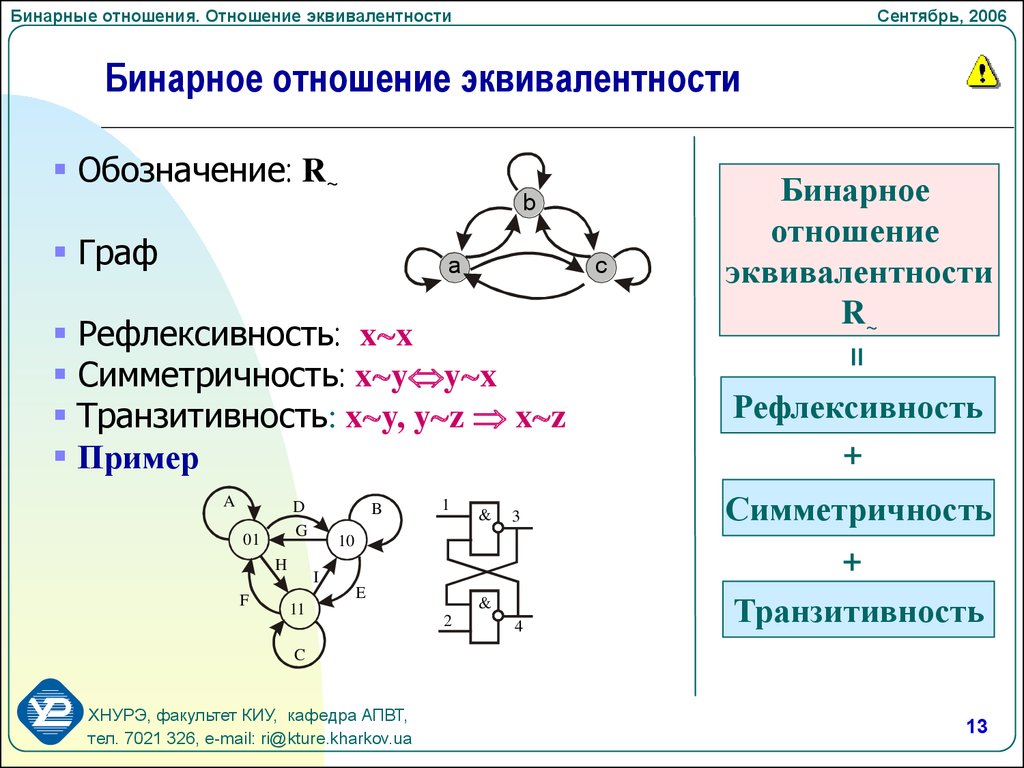

Изучайте взаимосвязь рефлексивности с другими свойствами: симметрией и транзитивностью.

Обратите внимание на специальные случаи, например, рефлексивные отношения в числовых множествах.

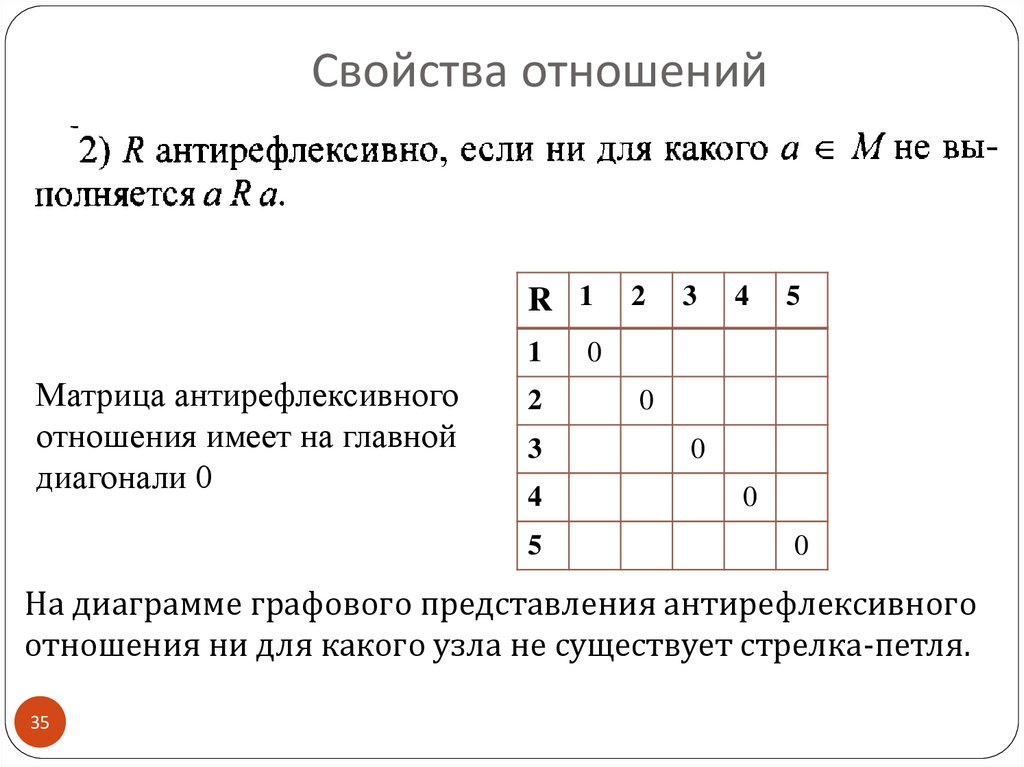
Применяйте рефлексивность на практике, например, в теории графов или реляционных базах данных.


Используйте простые множественные диаграммы Венна, чтобы визуализировать отношения между элементами.

Чаще проверяйте свои знания, решая тестовые вопросы и изучая дополнительные материалы.

Отношения. Свойства