Как правильно использовать арифметические корни и их свойства в математике
Арифметический корень степени n — это одна из основных операций в математике, широко применяемая в различных областях науки и техники. Важно правильно понимать его свойства, чтобы эффективно решать задачи. На этой странице собраны ключевые аспекты и полезные советы для работы с такими выражениями.


Не забывайте, что корень степени n существует только для положительных чисел, если n четное, и для всех чисел, если n нечетное.

АРИФМЕТИЧЕСКИЙ КОРЕНЬ n-ой СТЕПЕНИ свойства арифметического корня

Арифметический корень степени n можно записать как x^(1/n), что является обратной операцией возведения в степень.

Корень степени n и его свойства

Для извлечения корня из произведения двух чисел, воспользуйтесь свойством: √(a*b) = √a * √b.

11 класс, 6 урок, Свойства корня n-й степени

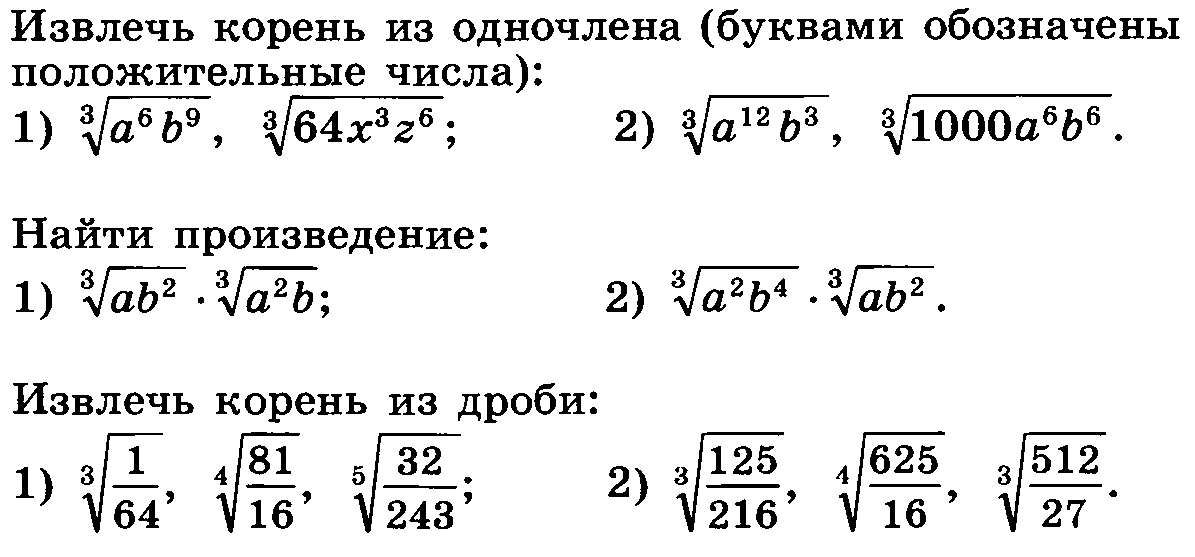
Чтобы извлечь корень из дроби, воспользуйтесь свойством: √(a/b) = √a / √b.

Как вычислять корни без Калькулятора ЕГЭ Математика 2018

Если степень n является четной, то корень из отрицательного числа не существует в множестве действительных чисел.

Корень n-ой степени. Алгебра, 9 класс

Для упрощения выражений с корнями можно использовать свойства, такие как √a^n = a^(n/2), если n четное.

При вычислении корней большого порядка рекомендуется использовать численные методы или калькуляторы для точности.
Свойства арифметического квадратного корня. 8 класс.
Помните, что арифметический корень степени 1 из любого числа всегда равен самому числу.

Свойства арифметического корня n-степени. Алгебра 9-класс
Чем больше степень корня, тем менее чувствительны результаты к изменению исходного числа.

Повысь свой уровень по теме КОРНИ - Математика - TutorOnline

Для упрощения вычислений с корнями используйте рациональные приближения или приближенные методы, такие как разложение в ряд Тейлора.

