Сколько касательных можно провести к двум окружностям и как это зависит от их положения

В данной статье мы рассмотрим, сколько общих касательных можно провести к двум окружностям, а также в каких случаях их может быть 0, 1, 2 или Понимание этого вопроса важно как для школьной геометрии, так и для практических задач в математике и физике.

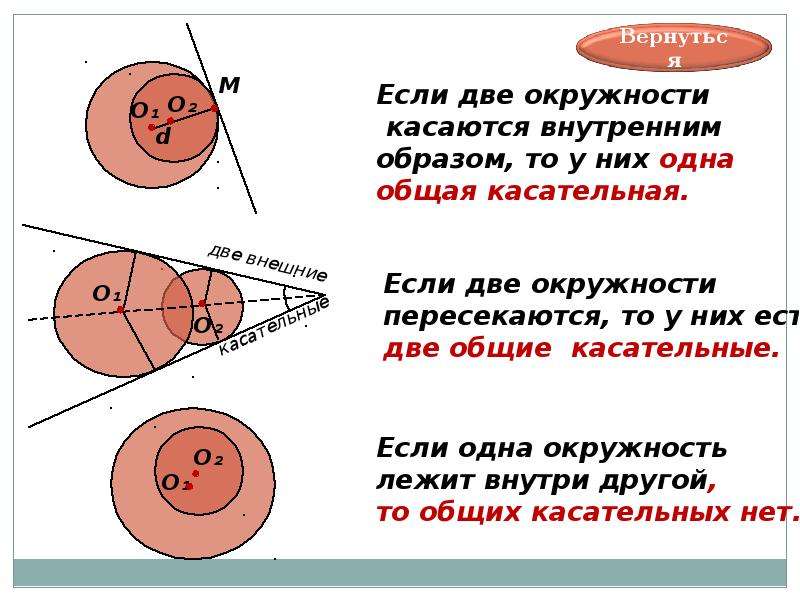
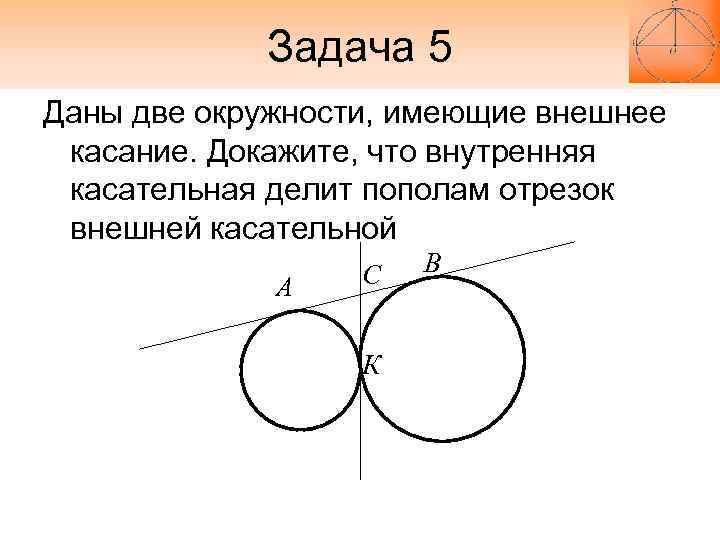
Чтобы найти количество общих касательных, нужно сначала определить взаимное расположение окружностей: они могут быть внешними, внутренними или иметь общие точки.

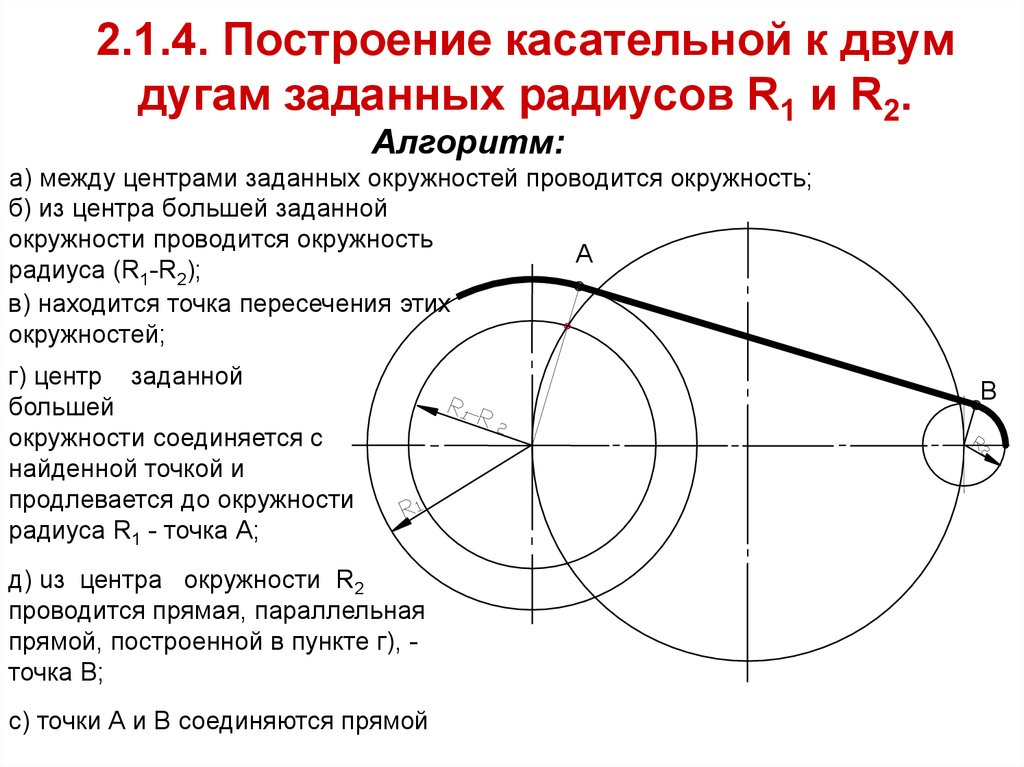
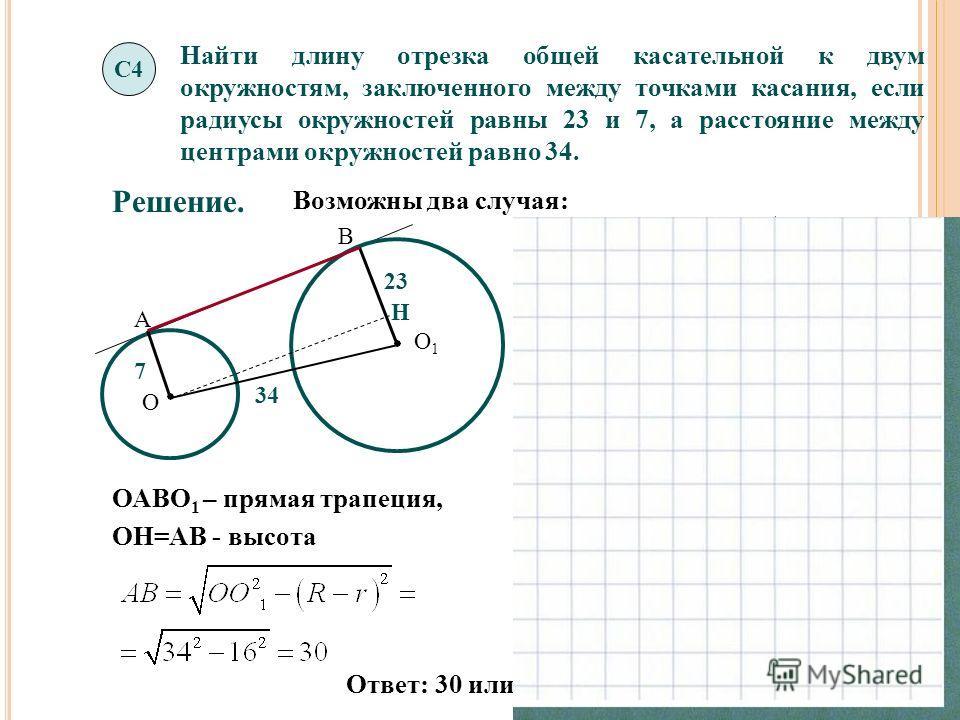
Если окружности не пересекаются и не касаются друг друга, то можно провести 4 общие касательные — две внешние и две внутренние.

Если окружности касаются друг друга внешне, то существует только 3 касательные — две внешние и одна общая касательная в точке касания.

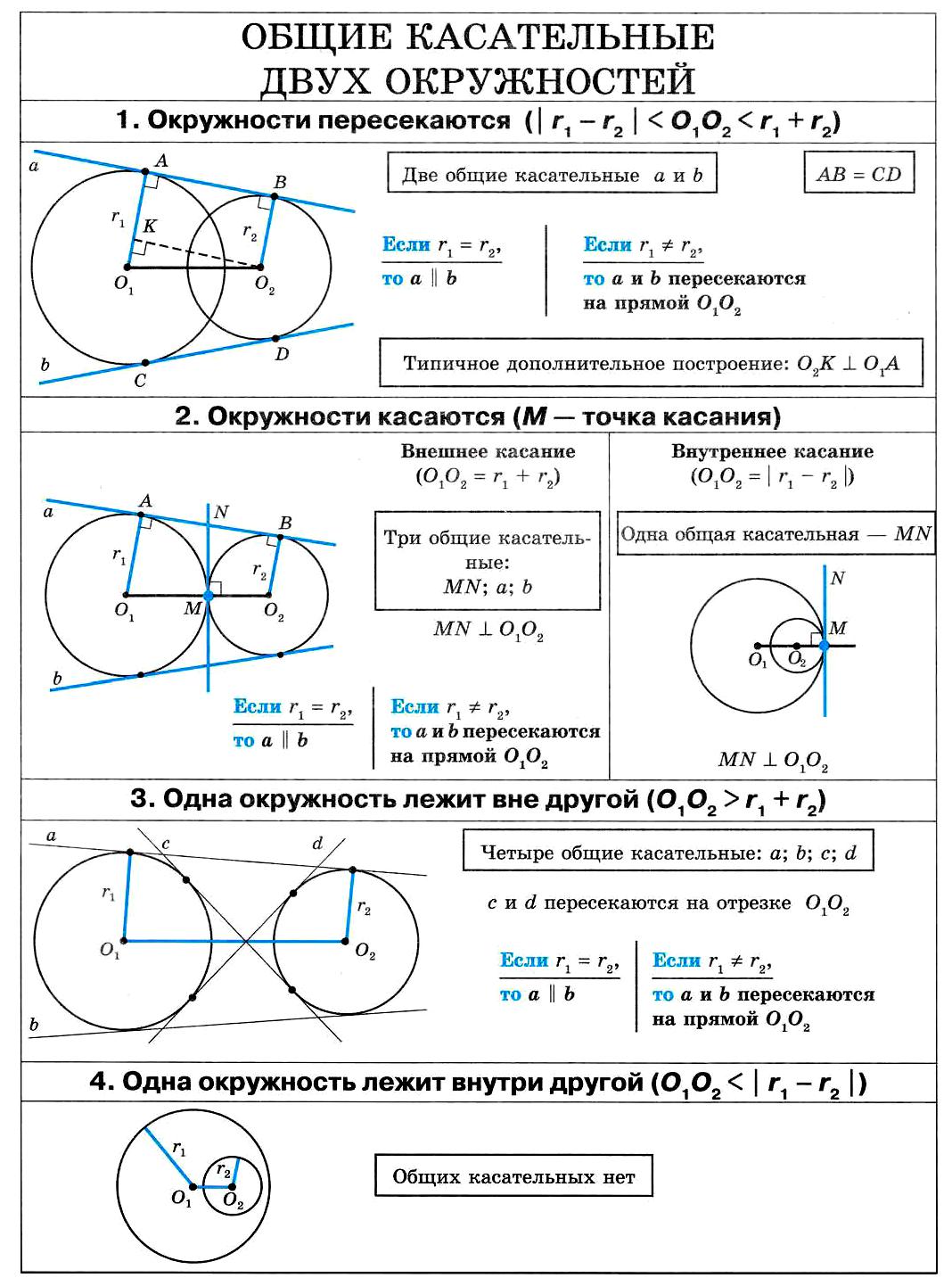
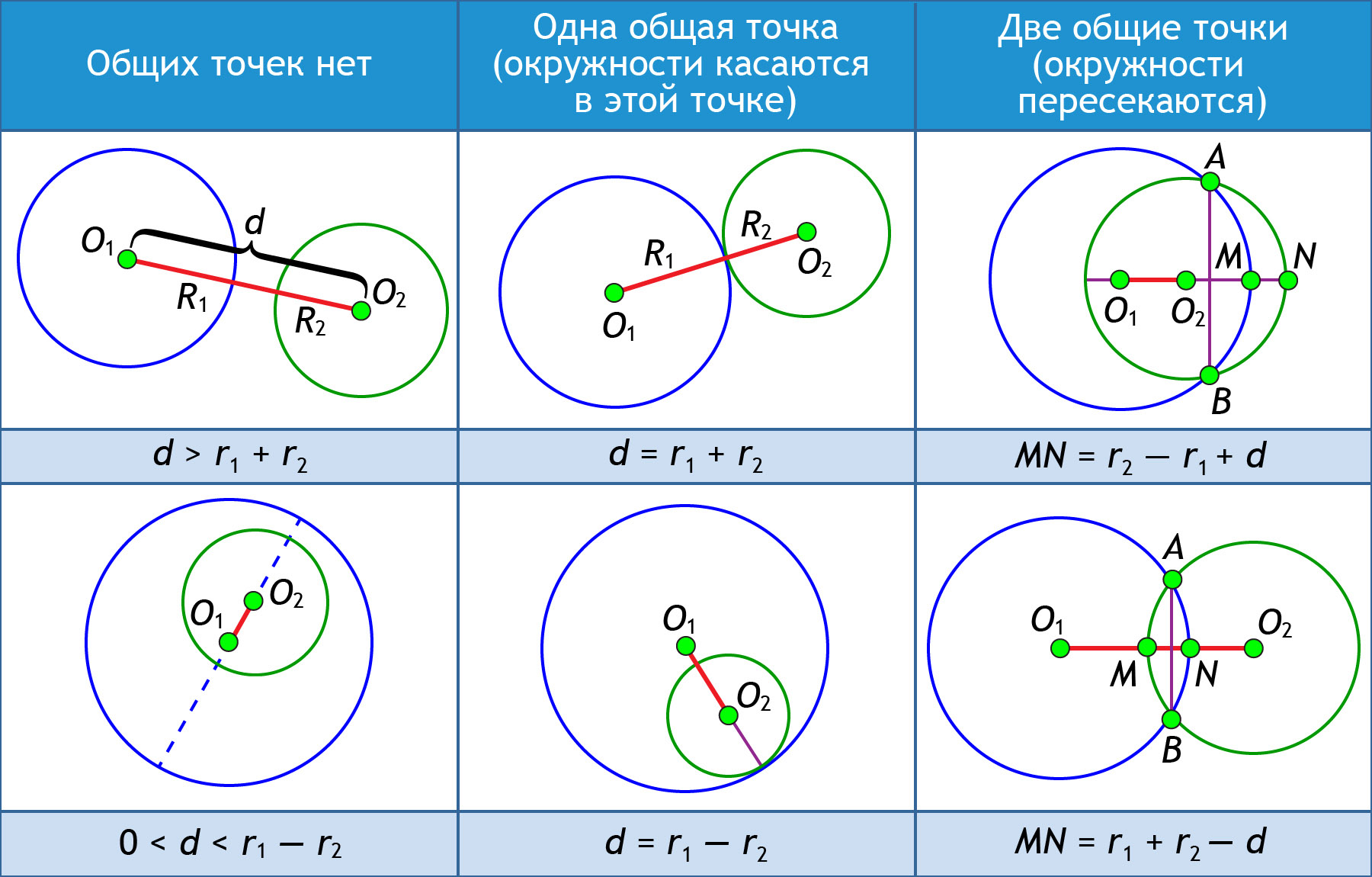
В случае, когда окружности касаются друг друга внутренне, также можно провести 3 касательные — две внешние и одна внутренняя.

Если окружности имеют общую точку, но не пересекаются, то существует только 2 внешние касательные.

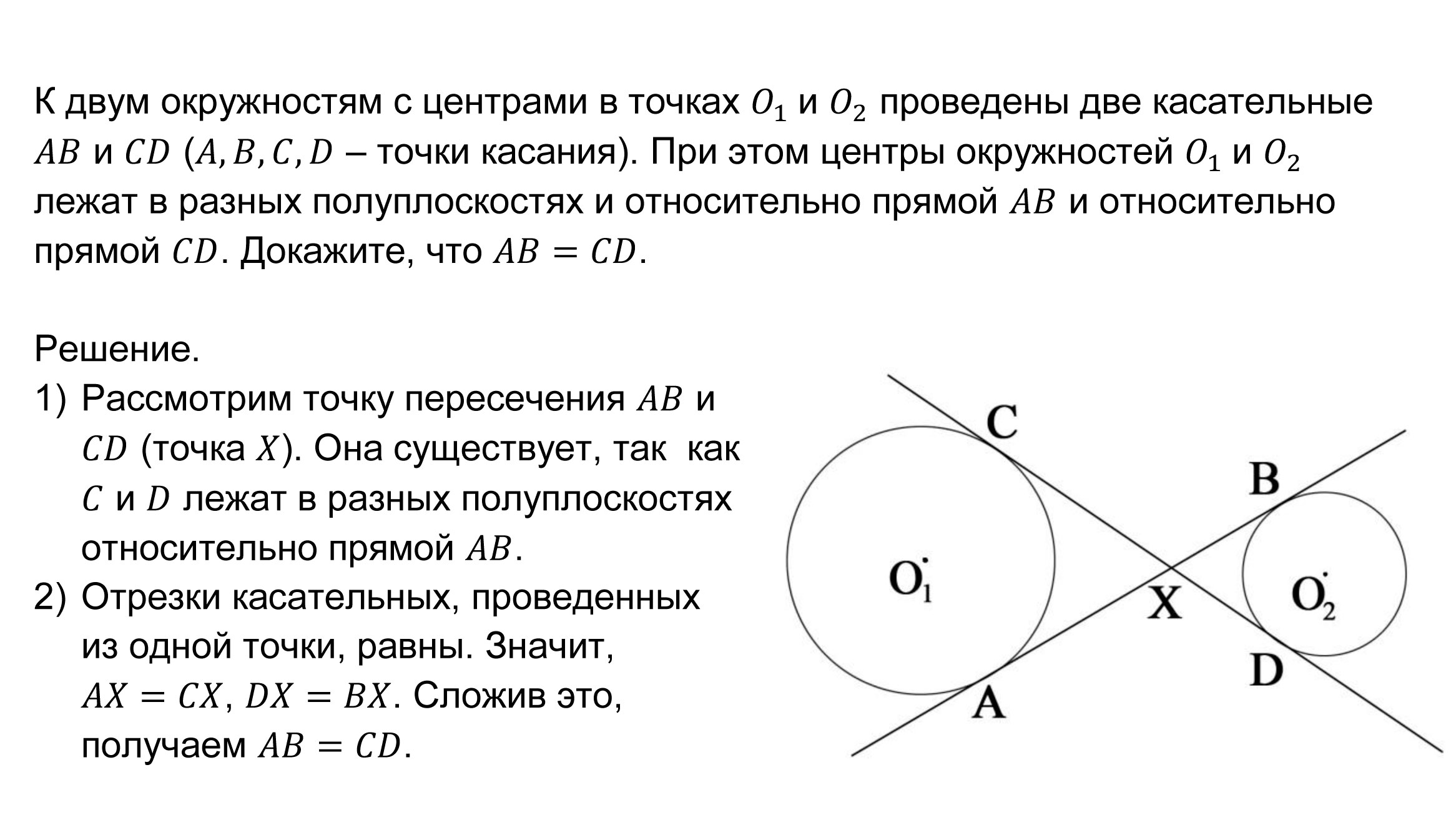
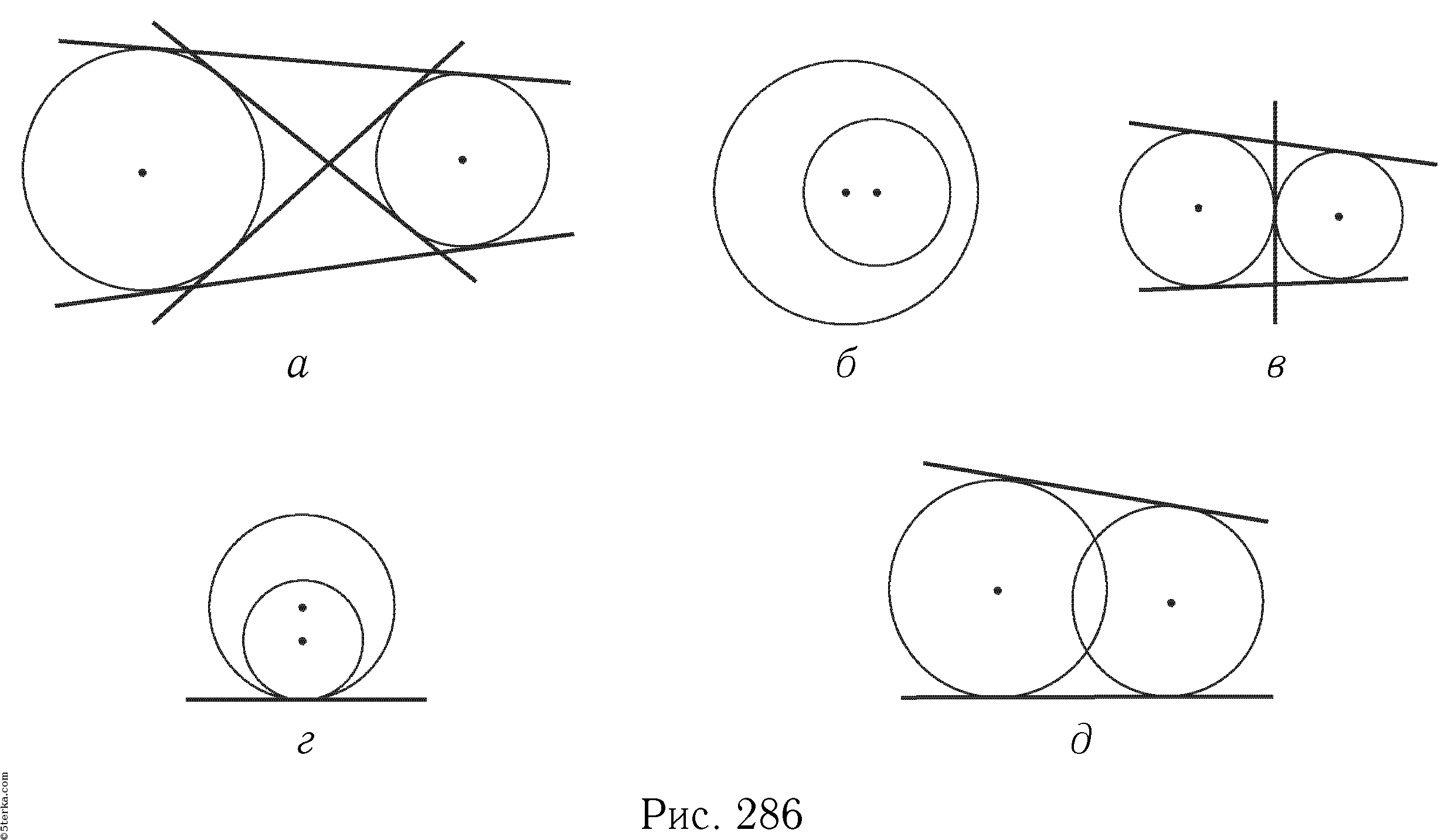
Когда окружности находятся в одной точке и пересекаются, это дает 2 общие касательные, при этом одна из них будет внутренней.

В случае, если окружности совпадают, существует бесконечное количество касательных, так как все касательные будут одинаковыми.

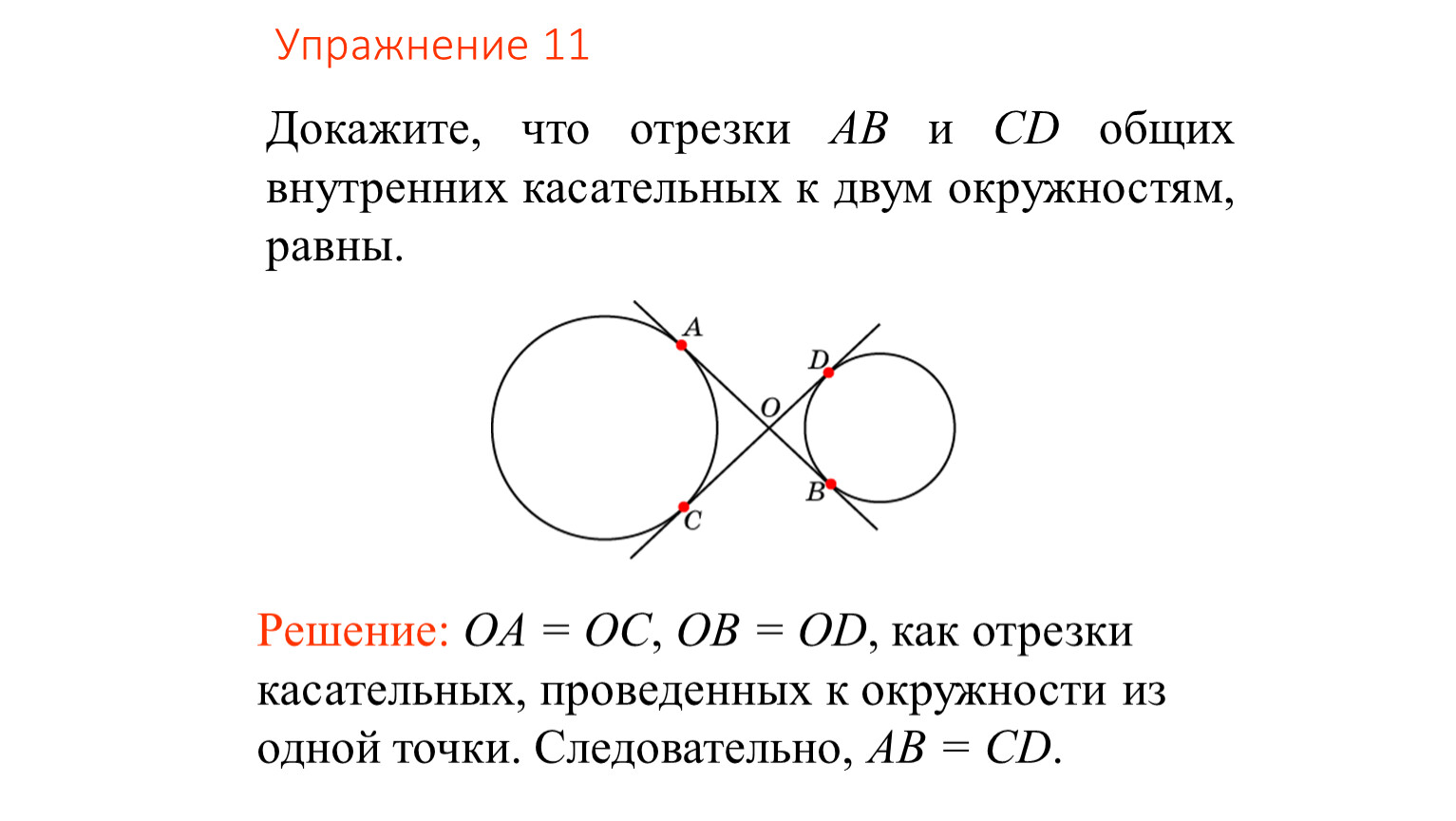
Для анализа расположения окружностей используйте радиусы и расстояние между центрами — это ключевые параметры для определения количества касательных.

В геометрии существует формула для нахождения расстояния между центрами окружностей, которая помогает точно определить тип их расположения и количество касательных.

Не забывайте, что для каждой ситуации существует свой метод доказательства количества касательных — используйте теорему о касательных или прямые уравнения для решения задач.