Рисование графов по степеням вершин: шаги и советы для начинающих
В этой статье представлены основные подходы к построению графов, где ключевую роль играет степень каждой вершины. Мы обсудим, как правильно интерпретировать данные о степенях и использовать их для визуализации графов, а также поделимся полезными советами по улучшению процесса рисования.
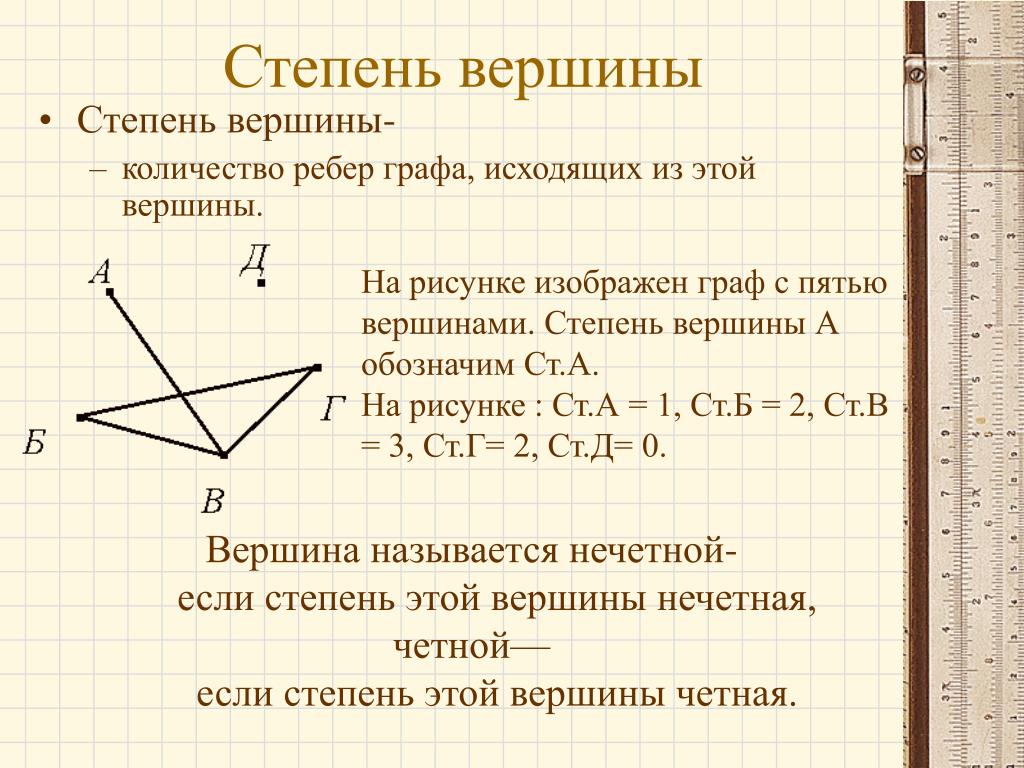
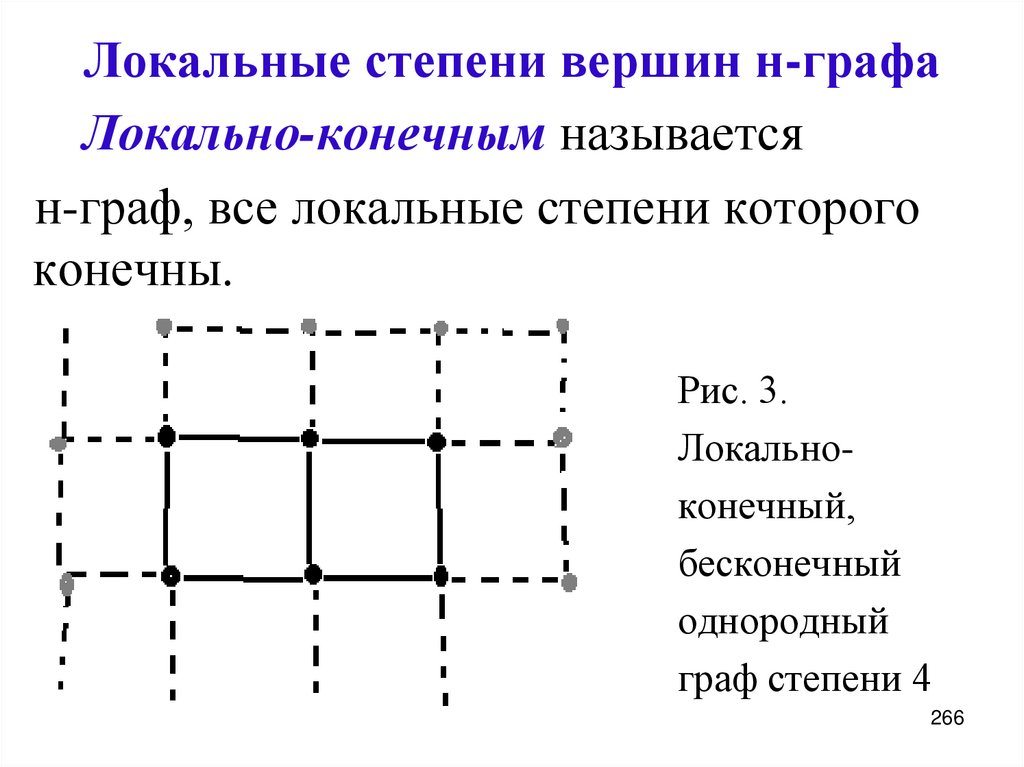
Начните с простых примеров: рисование графов с небольшим количеством вершин поможет понять базовые принципы.

Теория графов. Найти количество двудольных графов с 6 вершинами и 6 рёбрами (два подхода).
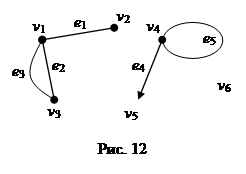
Обратите внимание на баланс степеней: для правильного рисования графа важно, чтобы сумма степеней всех вершин была четной.
Нумерация вершин в ориентиованном графе.
Используйте алгоритмы, такие как жадный алгоритм или алгоритм Ловаса, для упрощения процесса распределения степеней по вершинам.
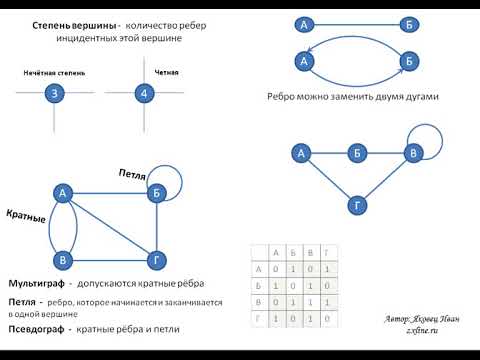
Графы, вершины, ребра, инцидентность, смежность
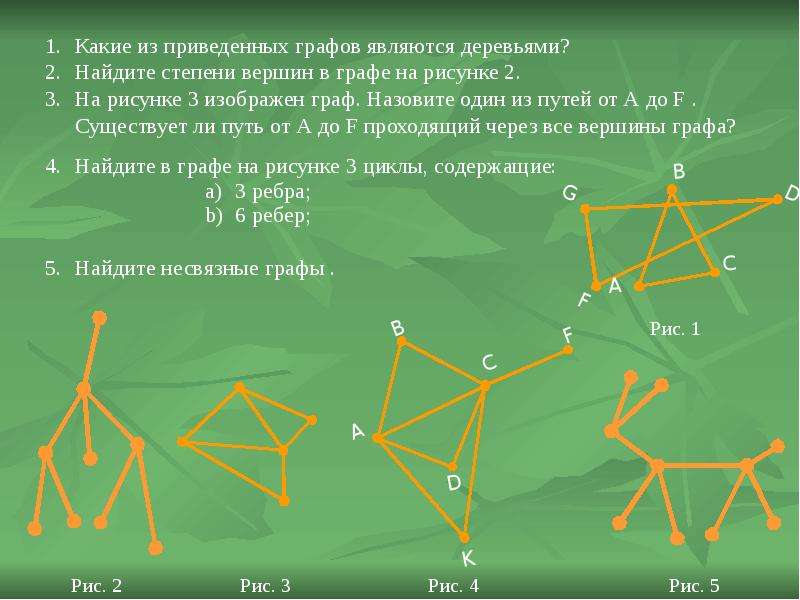

Не забывайте о симметрии: графы, где степени вершин распределены симметрично, могут быть более легко воспринимаемы визуально.

РАЗБОР ЗАДАЧИ - ТЕОРЕМА 1.

Применяйте цветовую кодировку для выделения различных степеней вершин, что улучшит восприятие структуры графа.

Основы теории графов. Связный граф. Дерево. Путь. Петля. Степень вершины. Цикл. 6 лекция
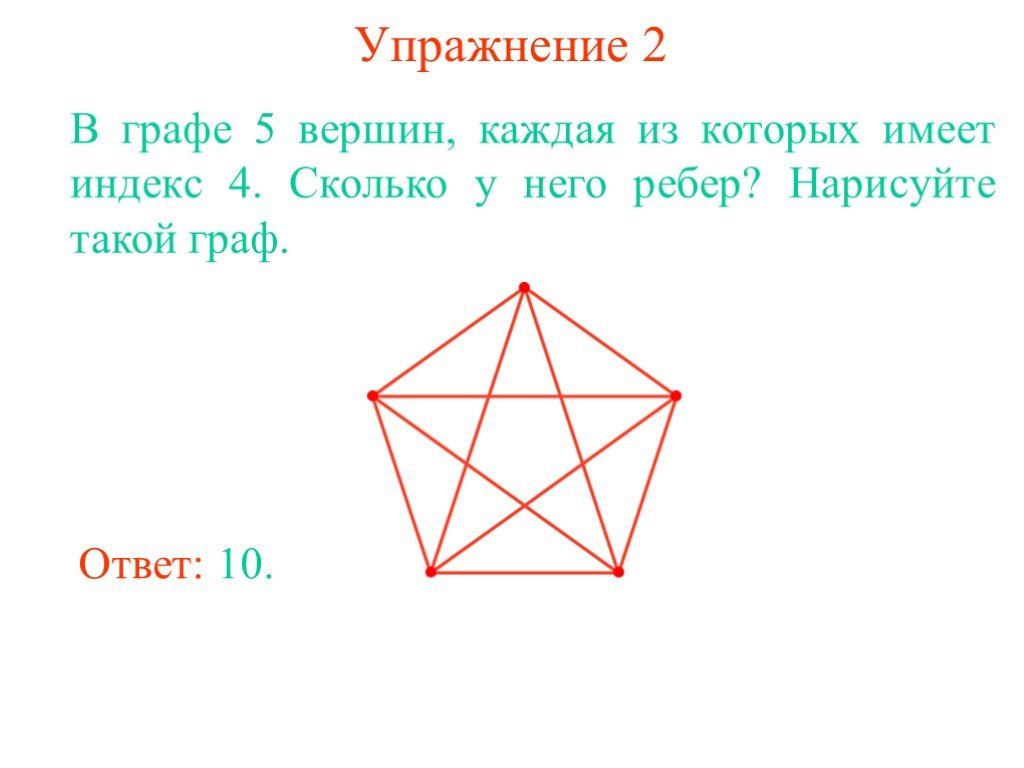
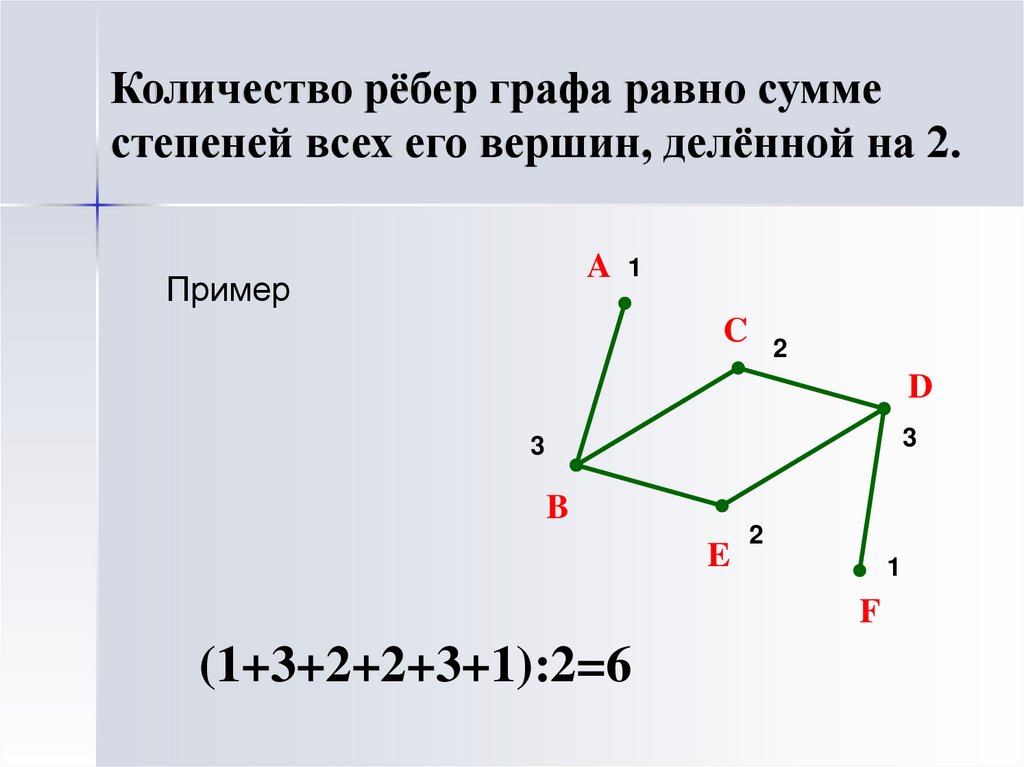
Используйте программные инструменты, такие как Gephi или Graphviz, для автоматизации процесса рисования и улучшения точности.

4.8 Степени вершин графов
Проверяйте полученные графы на наличие избыточных рёбер и корректность структуры: граф должен быть связным и соответствовать заданным степеням.
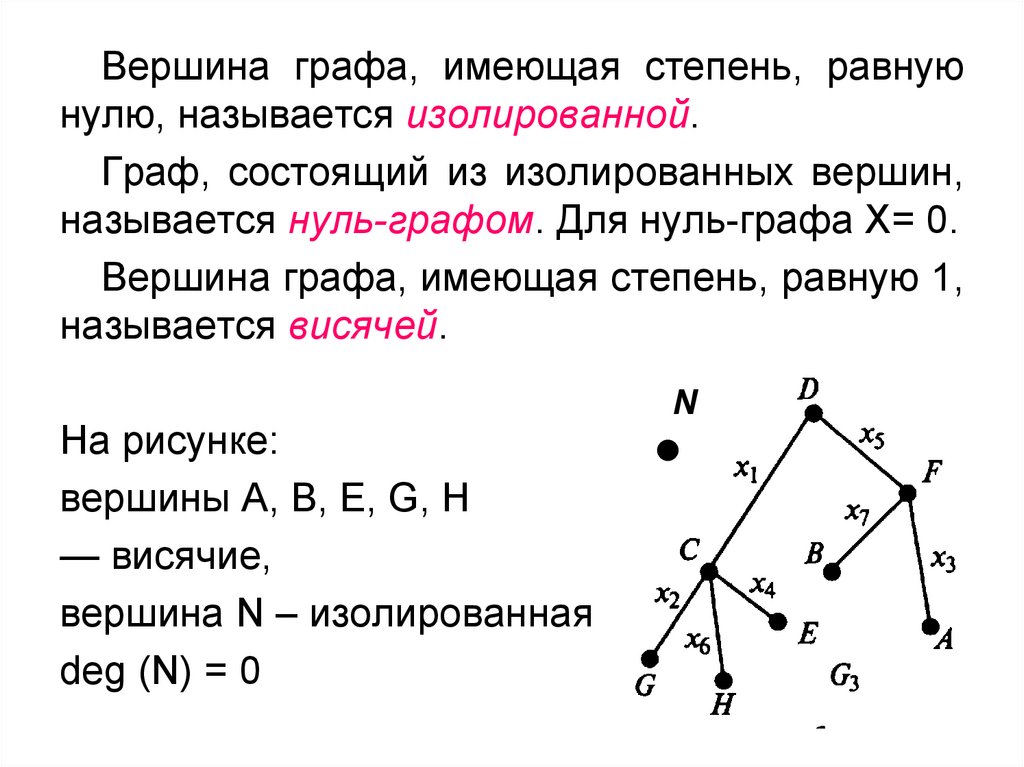
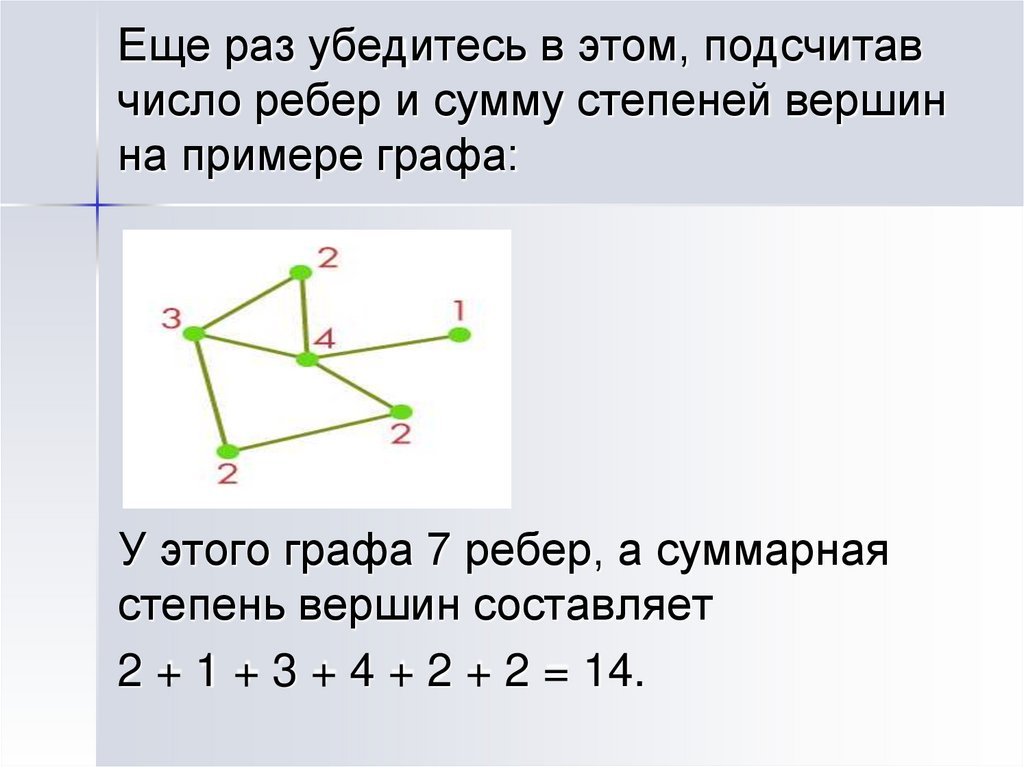
Применяйте различные формы графов (например, направленные или ненаправленные), чтобы лучше визуализировать зависимости между вершинами.
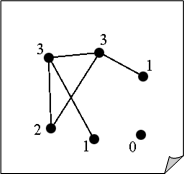
Пробуйте использовать разные алгоритмы укладки графов для улучшения читаемости и визуальной эстетики, например, алгоритм ФР или Репульс.

Графы. Основные понятия
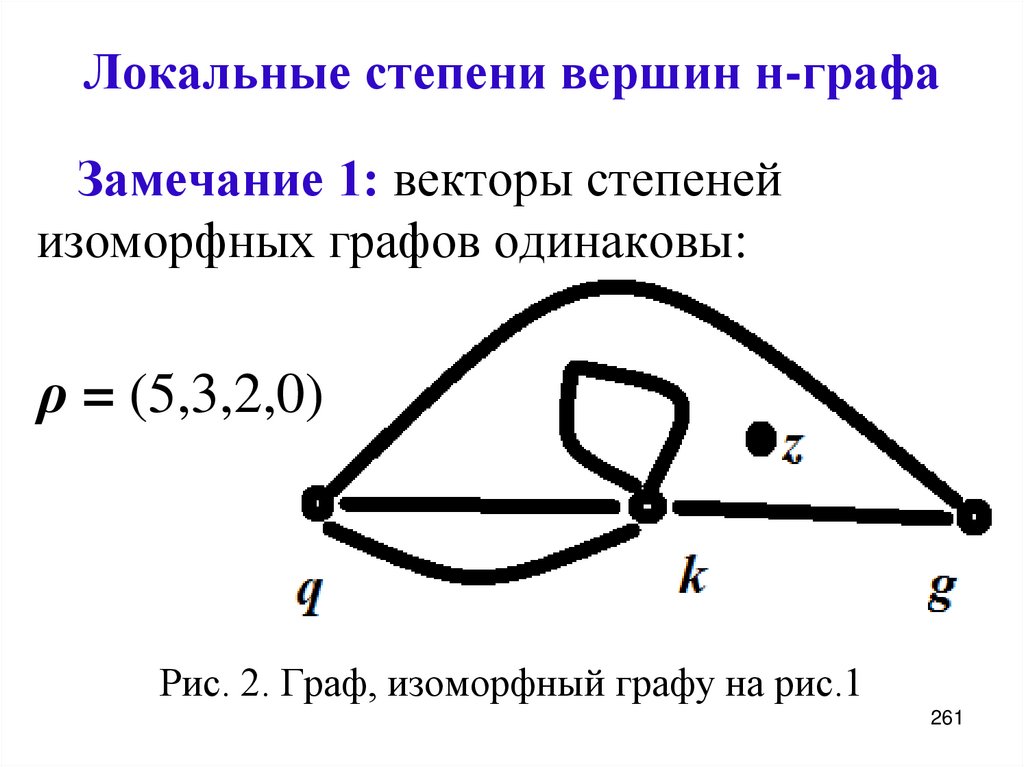
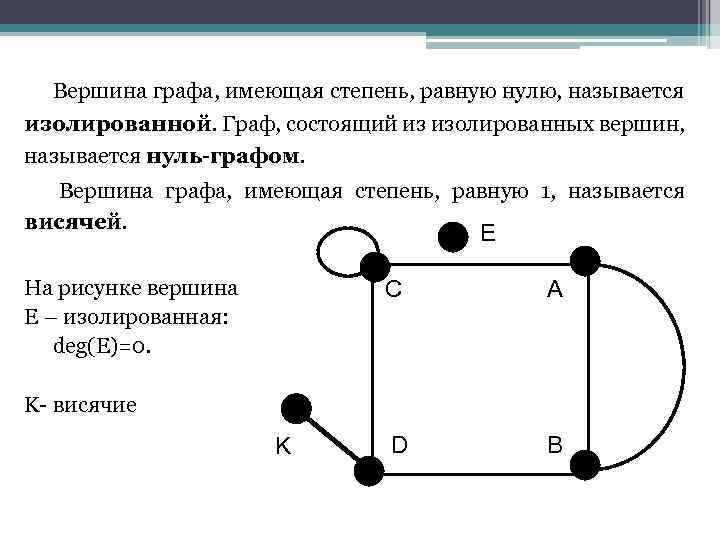
Не забывайте о возможных ошибках: убедитесь, что каждая вершина имеет правильное количество рёбер, соответствующее её степени.
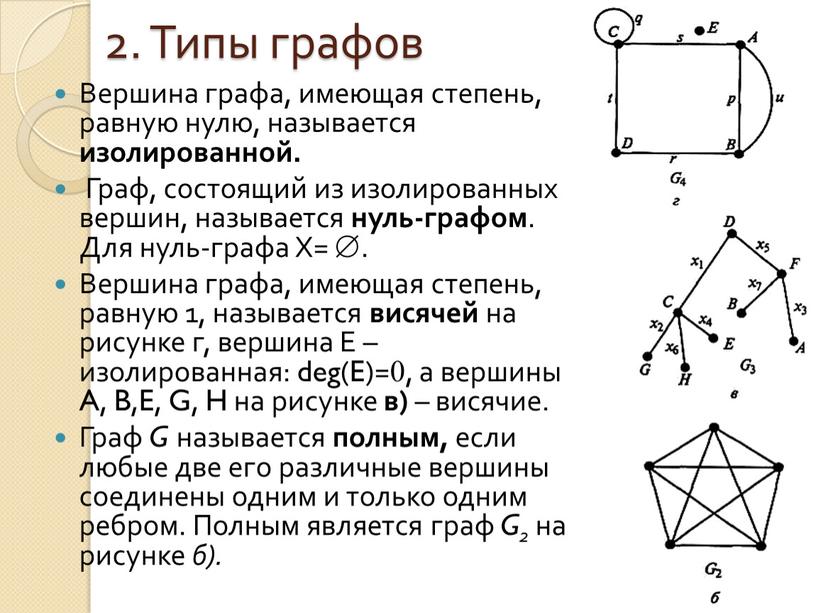

Лекция 8. Основы теории графов