Полный гид по построению графика функции y = x² для начинающих
В этом разделе вы найдете полезные советы по построению графика функции y = x², а также рекомендации для правильного понимания ее свойств. Мы расскажем о ключевых моментах, таких как вершина, оси симметрии и поведение графика, чтобы вы могли легко и быстро освоить этот важный математический процесс.

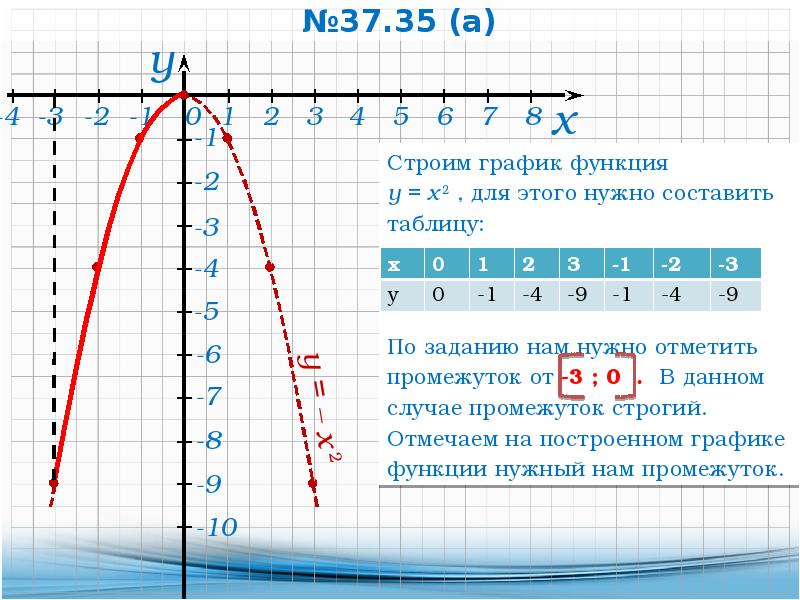
Начните с того, чтобы определить точку, в которой график пересекает ось Y, что для функции y = x² всегда будет точка (0, 0).
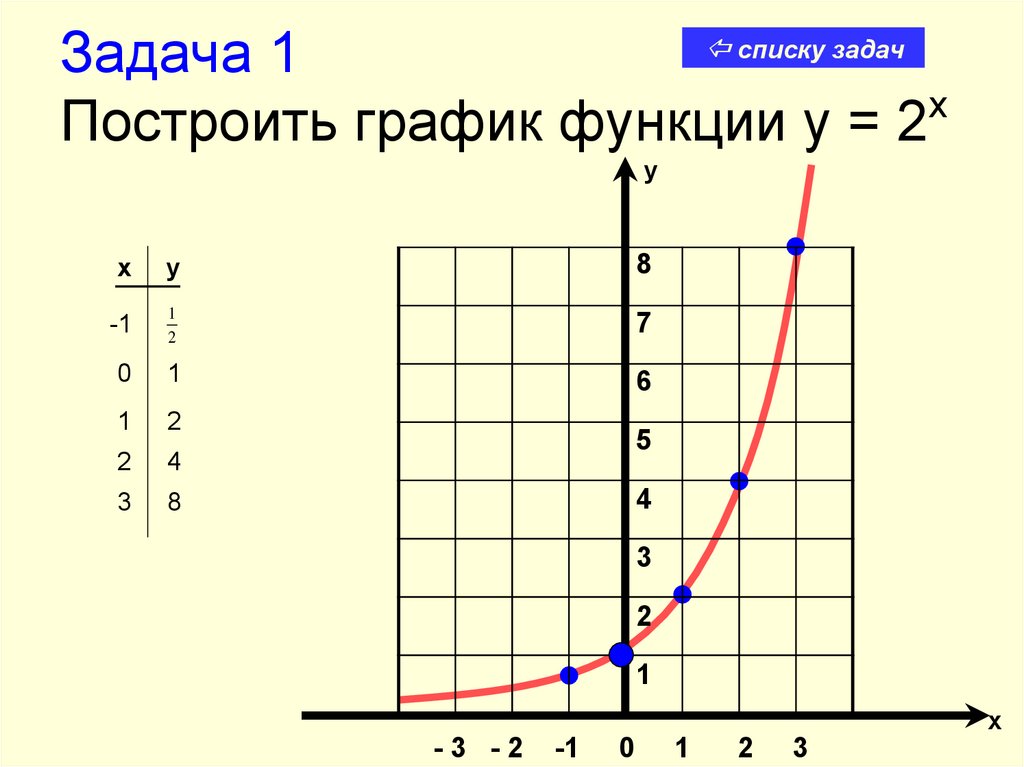
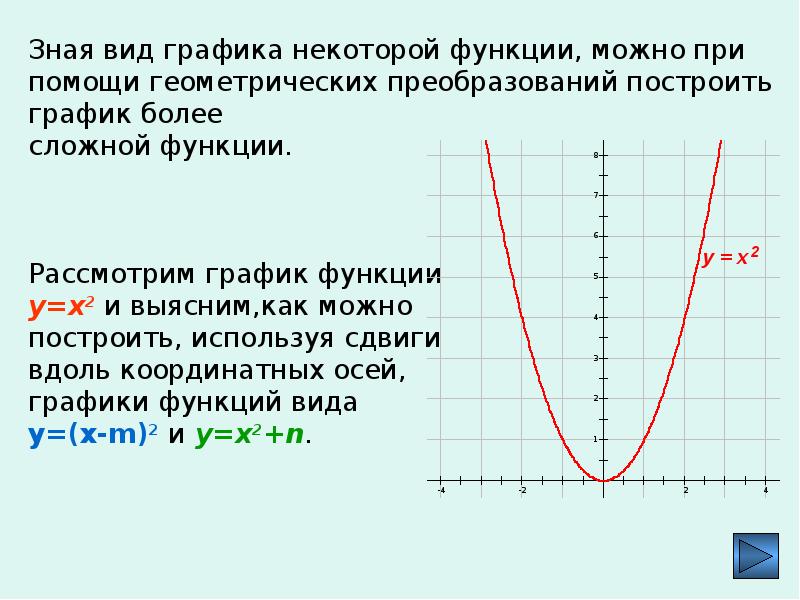
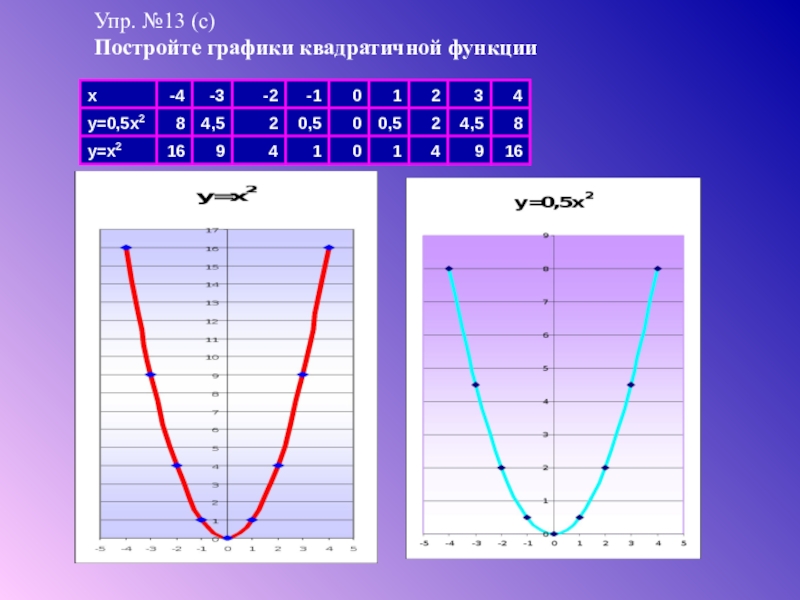
График функции y=x² (y=аx).
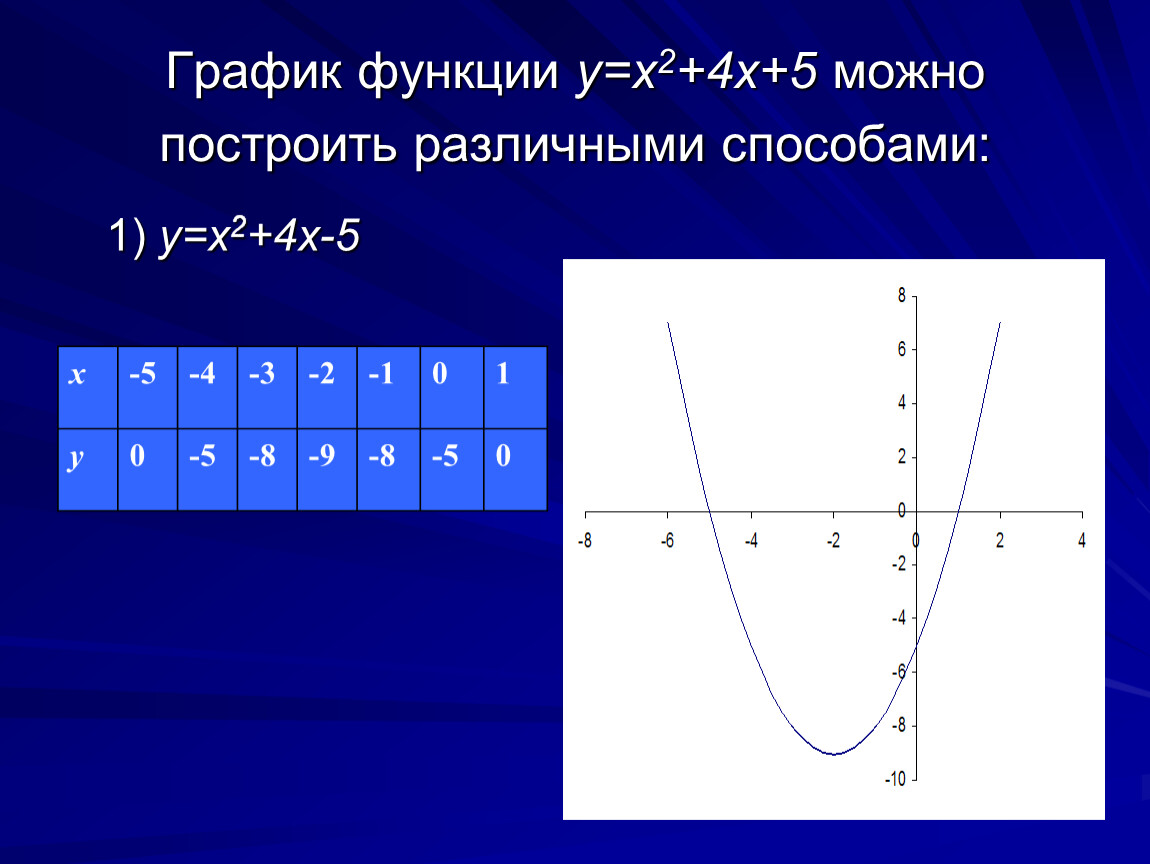
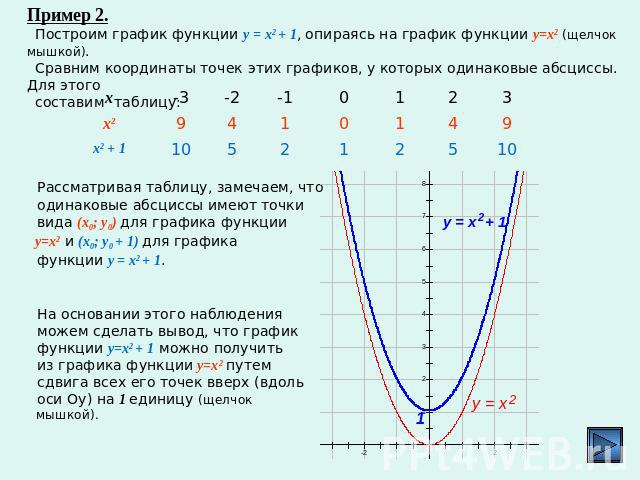
Помните, что график функции y = x² является параболой, открывающейся вверх. Это означает, что у нее всегда есть минимальное значение в вершине.

РАЗБОР варианта №5 из сборника Ященко ОГЭ по математике
Оси симметрии графика функции y = x² проходят через вертикальную линию x = 0. Это важно для правильного построения симметричных точек.
7 класс, 34 урок, Функция y=х^2 и её график
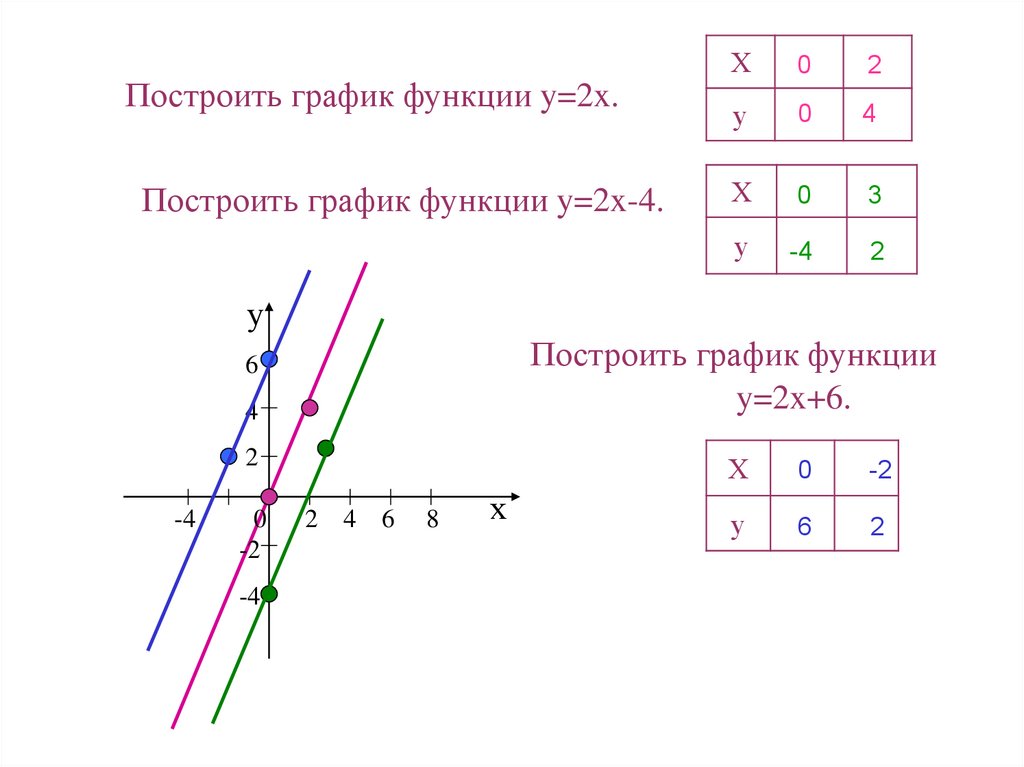
Для построения графика выберите несколько значений x, подставьте их в уравнение и вычислите соответствующие значения y. Эти точки помогут вам построить точный график.
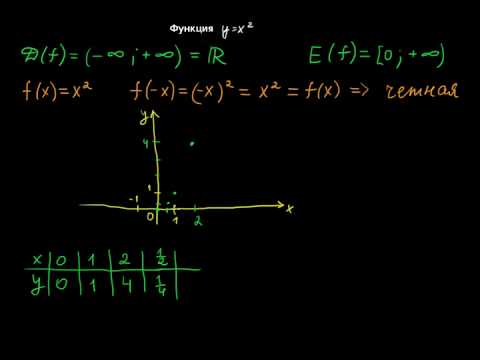
§77 Функция y=x²
Помимо точек пересечения с осями, график функции y = x² будет симметричен относительно оси Y, поэтому достаточно построить график для положительных значений x, а затем зеркально отобразить его для отрицательных значений.

§79 Преобразование графика функции y=x²
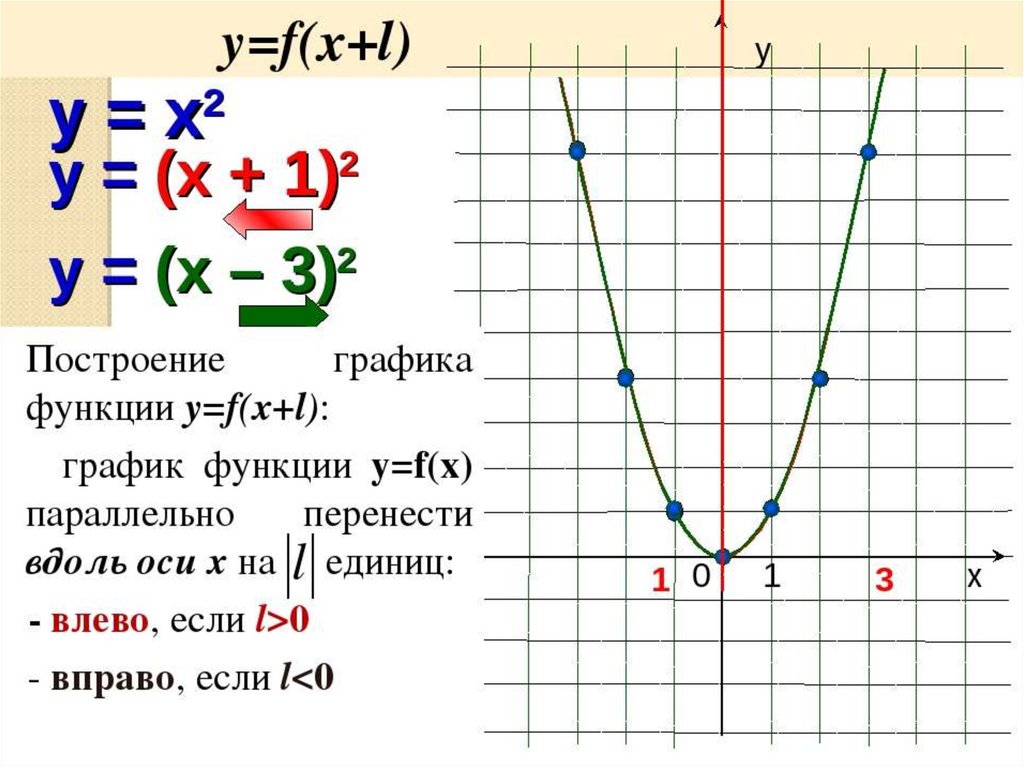
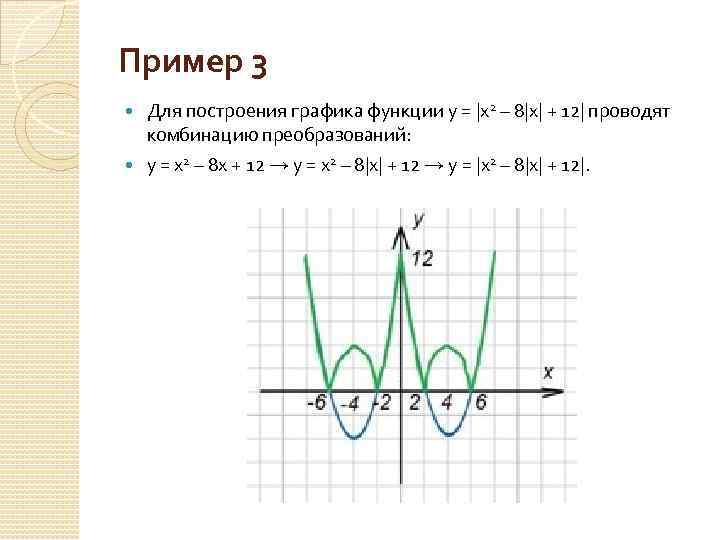
Обратите внимание, что при увеличении значения x (как в положительном, так и в отрицательном направлении), значения y растут быстрее, что делает график более крутым.
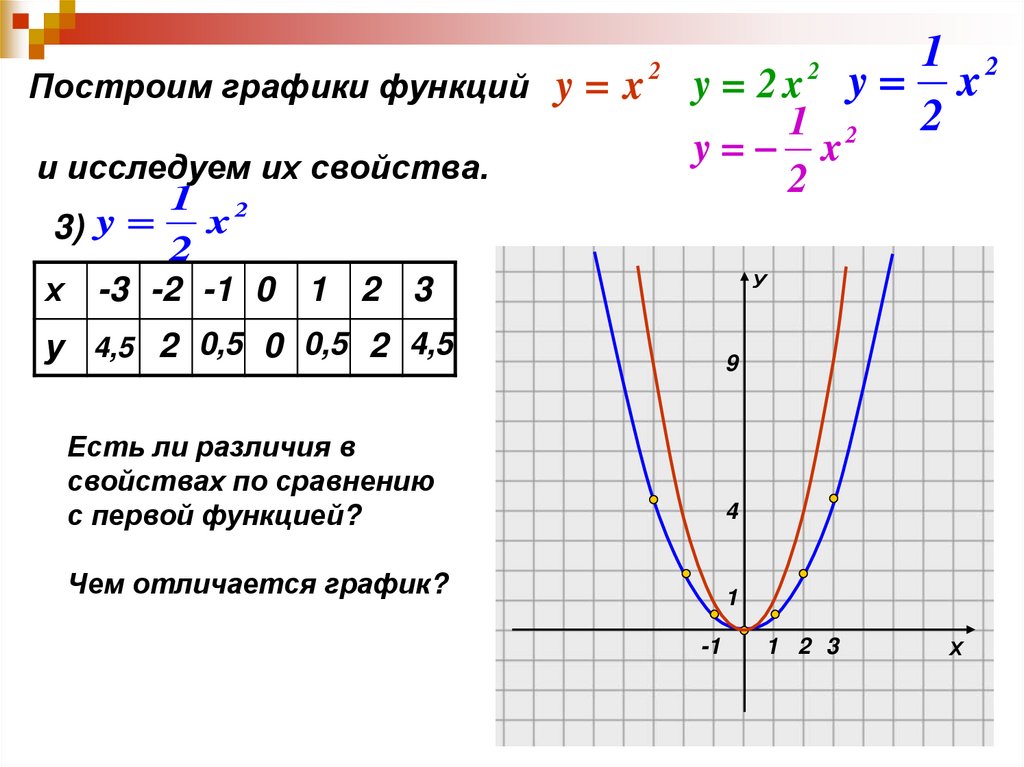
Чтобы облегчить построение графика, начертите сетку, чтобы четко видеть, где расположены точки на оси X и оси Y.

Функция у=х² и у=х³ и их графики. Алгебра, 7 класс
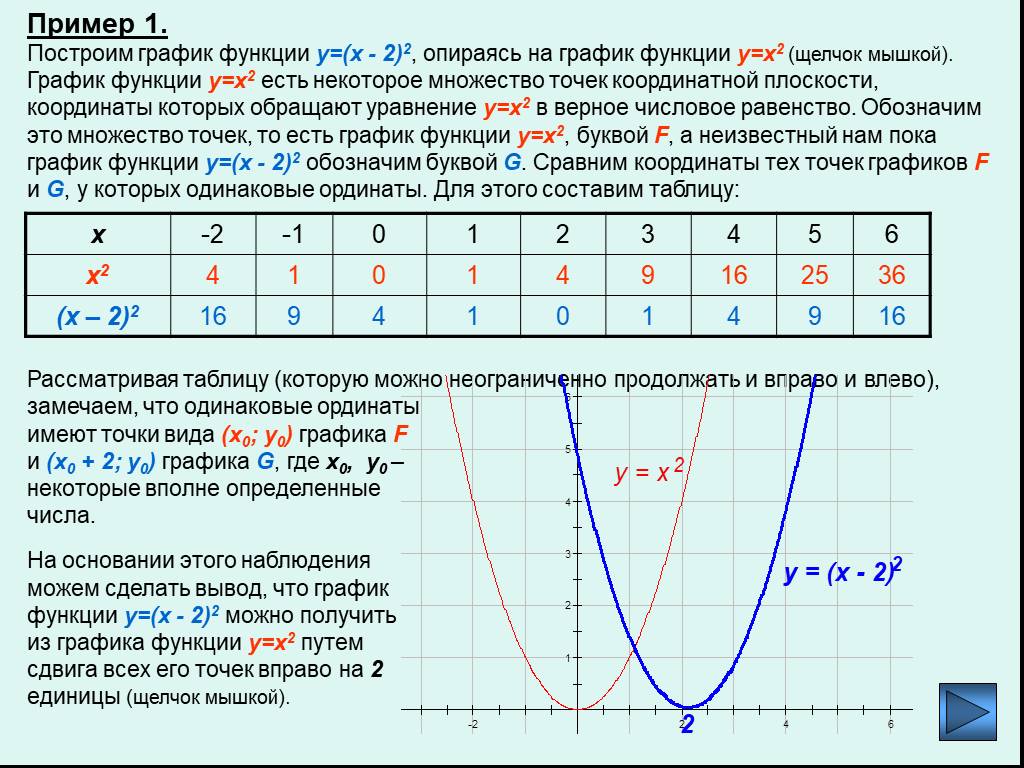
Использование различных значений x позволит вам увидеть, как функция ведет себя для разных диапазонов значений, что поможет более точно нарисовать параболу.
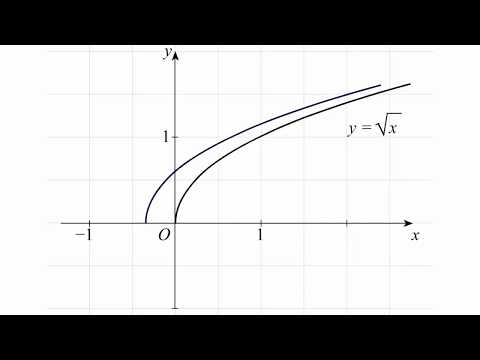
Построение графика функции y = 2x^2
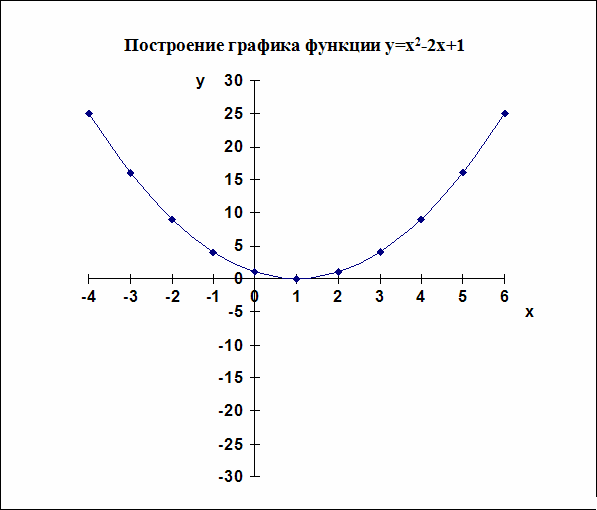
Для более точного построения попробуйте использовать калькулятор или графический редактор, который автоматизирует процесс вычислений и отображения графика.

Квадратичная функция за 5 минут
Помните, что для функции y = x² всегда существует только одна вершина, которая является минимальной точкой графика, и ее координаты (0, 0).
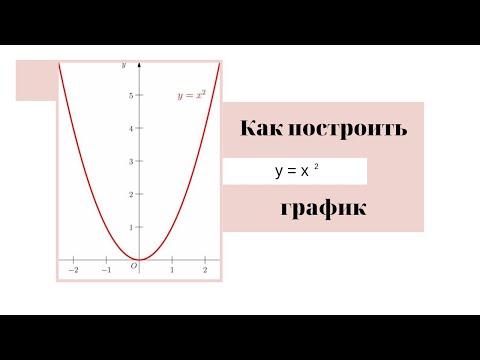
Построить график функции y=x2. Парабола.