Треугольник и его проекция: площадь на плоскости
На этой странице вы найдете подборку фотографий и советы по определению площади проекции треугольника на плоскость. Мы разберем ключевые моменты, формулы и наглядные примеры, которые помогут лучше понять и применить этот процесс.

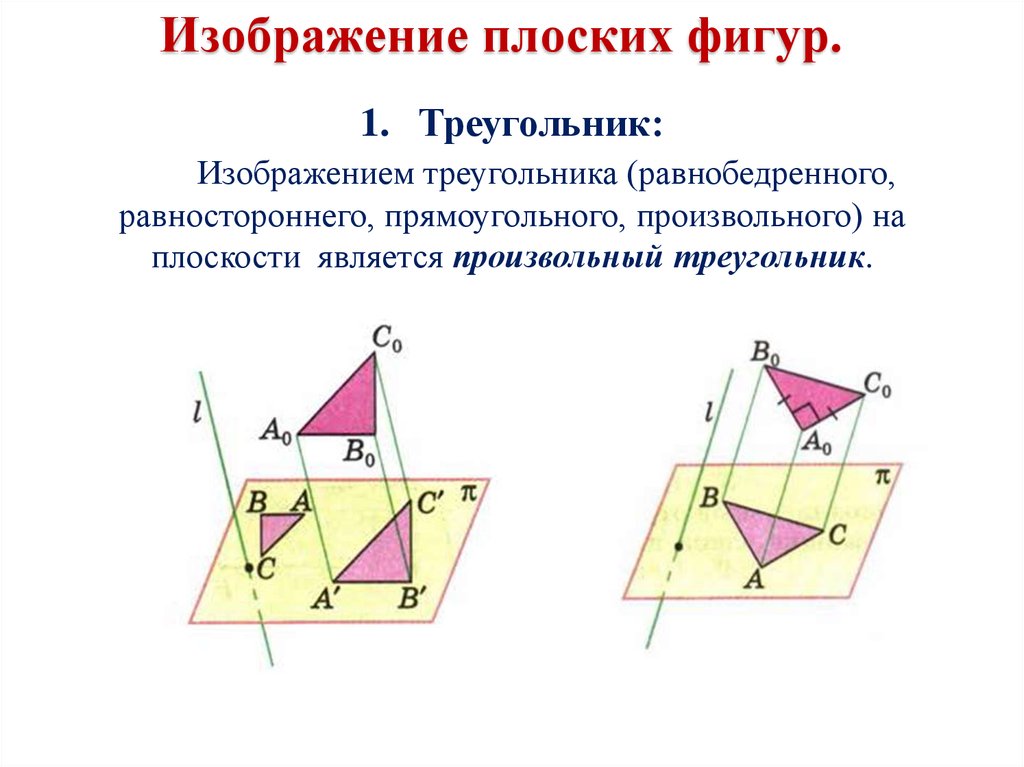
Начните с определения координат вершин треугольника в трехмерном пространстве.

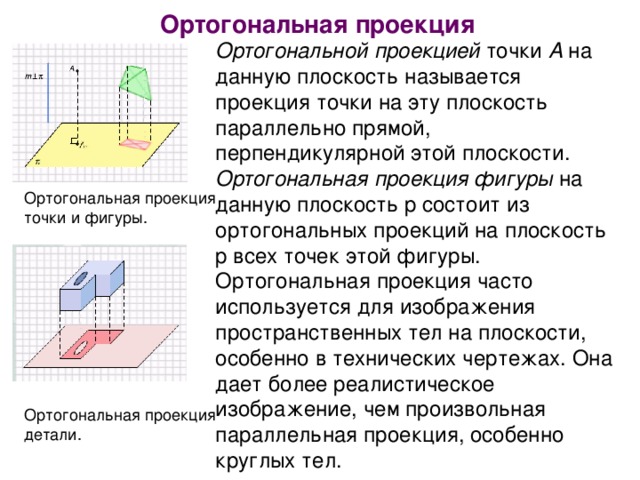
Ортогональная проекция и ортогональная составляющая. Тема
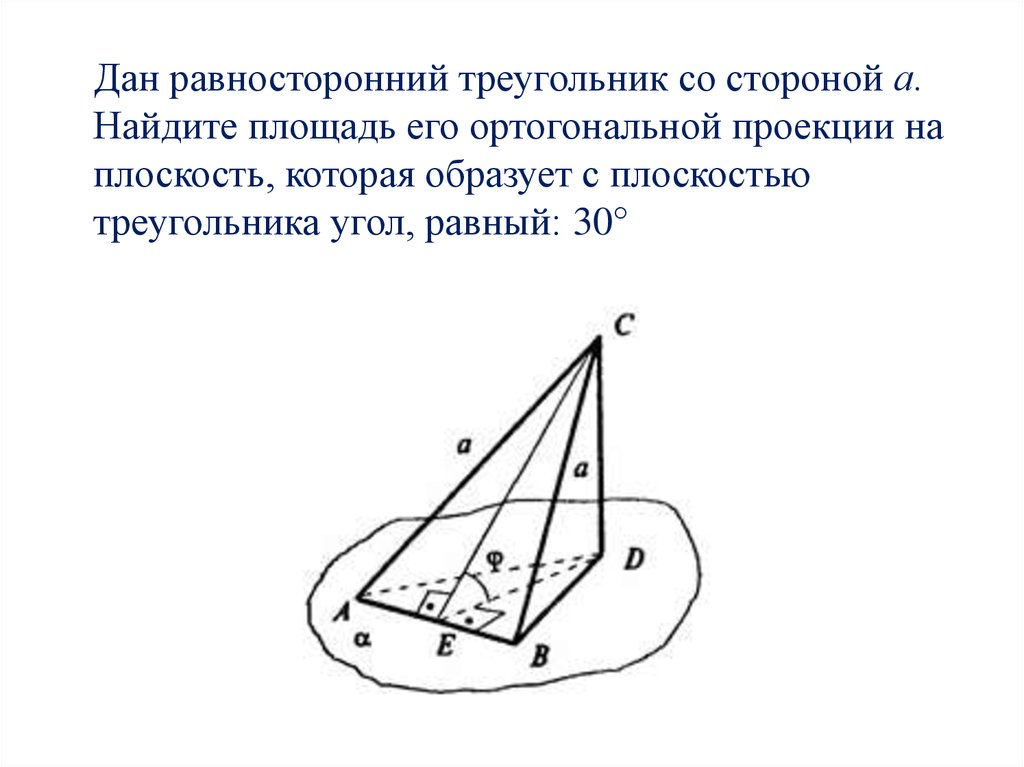
Для проекции треугольника выберите плоскость (XY, YZ или ZX), на которую будет проецироваться фигура.

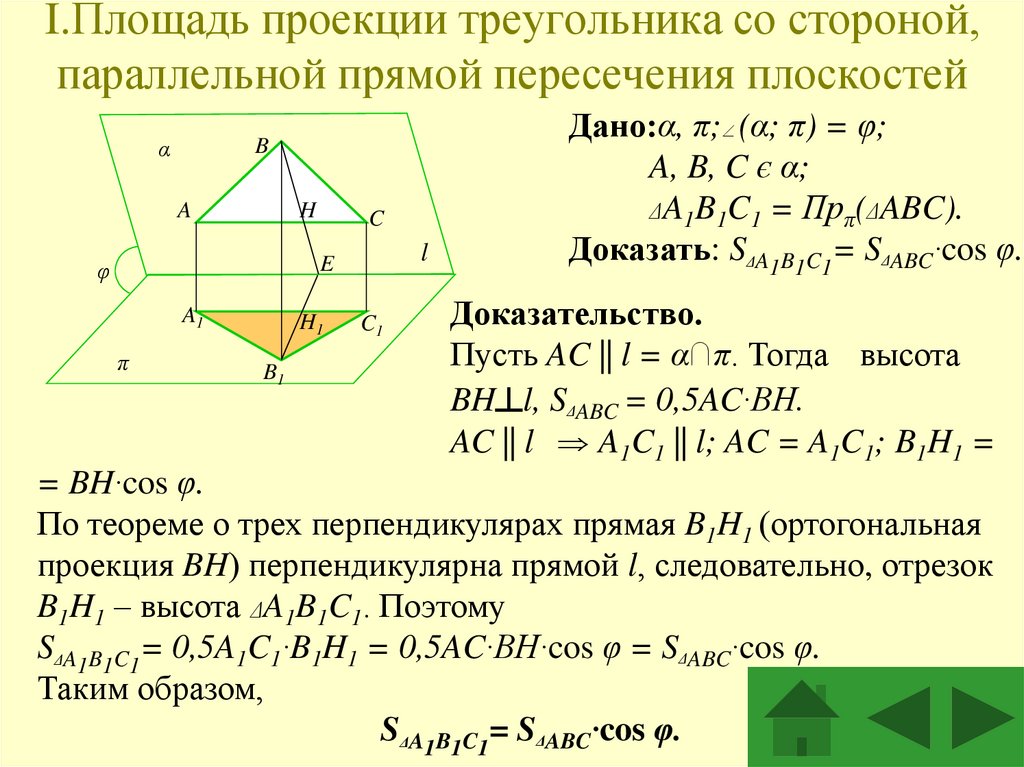
Площадь ортогональной проекции
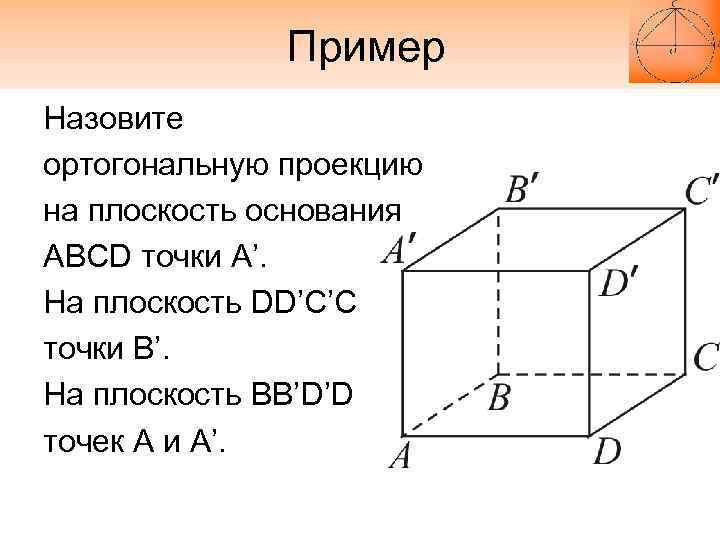
Используйте формулу для площади треугольника, основанную на координатах его вершин, например, через векторное произведение.

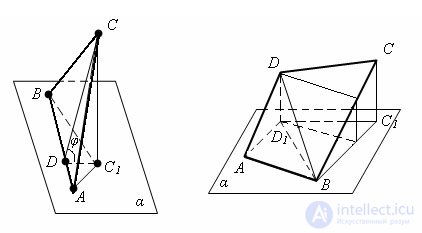
Определение натуральной величины треугольника АВС методом замены плоскостей проекции

Убедитесь, что при проекции правильным образом обнуляется одна из координат, соответствующая выбранной плоскости.

Пересечение двух плоскостей. Плоскости в виде треугольника
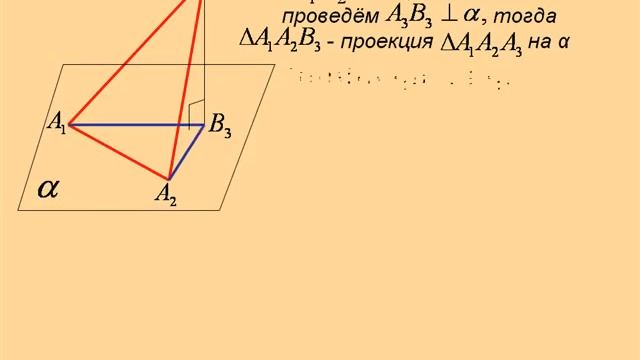
Для упрощения вычислений используйте графические программы или инструменты для 3D моделирования.

Площадь ортогональной проекции

Проверьте правильность результата, сравнив его с примером из учебника или другого достоверного источника.
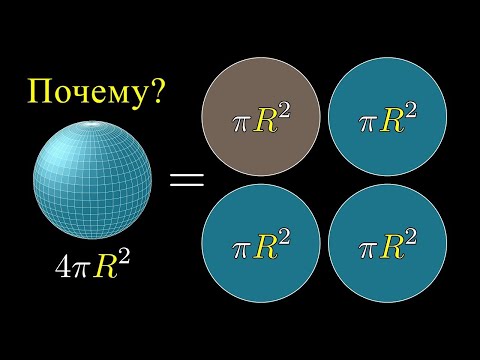
Почему площадь сферы в четыре раза больше её тени? [3Blue1Brown]
Если координаты сложны для ручного расчета, примените математическое ПО, такое как MATLAB или GeoGebra.
Рассмотрите использование нормального вектора для точного расчета площади на произвольной плоскости.
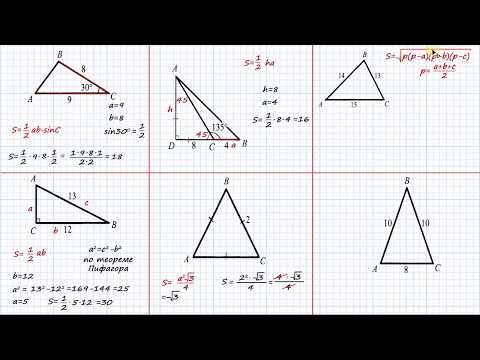
Найти площадь треугольника АВС. Задачи по рисункам
Используйте вспомогательные линии, чтобы визуализировать проекцию для лучшего понимания процесса.

Площадь ортогональной проекции многоугольника


Потренируйтесь на нескольких примерах разной сложности, чтобы закрепить навыки вычислений.
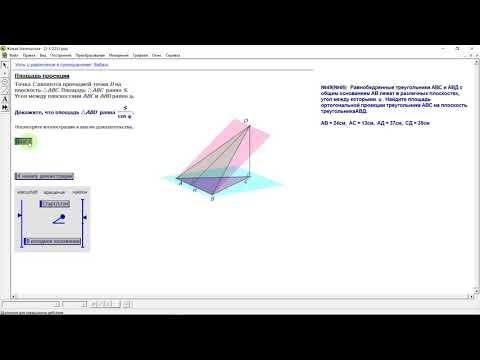
Геометрия 10 класс \