Обзор основных числовых множеств, используемых в математике для решения различных задач

На этой странице вы найдете разнообразные числовые множества, используемые в математике, а также их краткие описания. Мы предлагаем не только теоретические аспекты, но и практическое применение каждого множества в решении задач. Включены такие множества, как натуральные, целые, рациональные, иррациональные числа и другие.

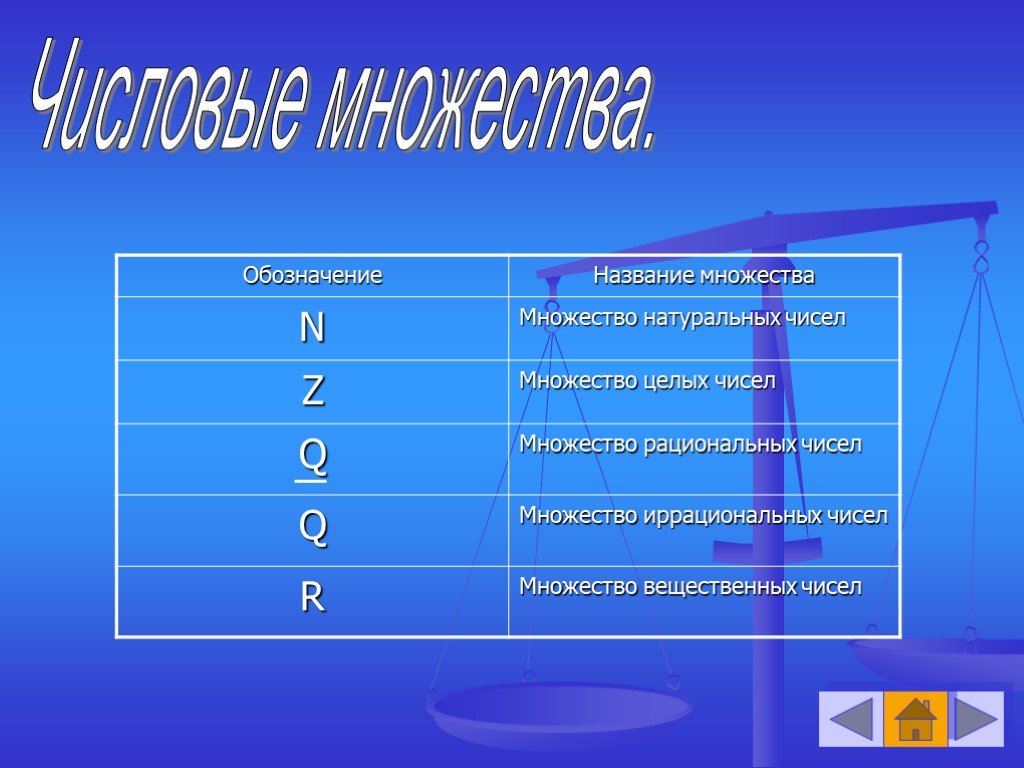
Запомните, что множество натуральных чисел начинается с 1 и продолжается до бесконечности, не включая отрицательных чисел и дробей.

Целые числа включают как положительные, так и отрицательные числа, а также ноль, что делает их основным инструментом при решении уравнений и неравенств.

Рациональные числа могут быть представлены в виде дроби, где числитель и знаменатель - целые числа. Важно, что рациональные числа могут быть как конечными, так и периодическими.

Иррациональные числа, в отличие от рациональных, нельзя записать в виде конечной дроби или дроби с периодической десятичной частью, примером таких чисел является число √2 или π.

Алгебраические числа – это числа, которые являются корнями многочленов с целыми коэффициентами. Например, √2 является алгебраическим числом, так как оно является корнем уравнения x² - 2 = 0.

Трансцендентные числа не являются корнями любых алгебраических уравнений. Примером таких чисел является число π, которое не может быть решением никакого многочлена с целыми коэффициентами.

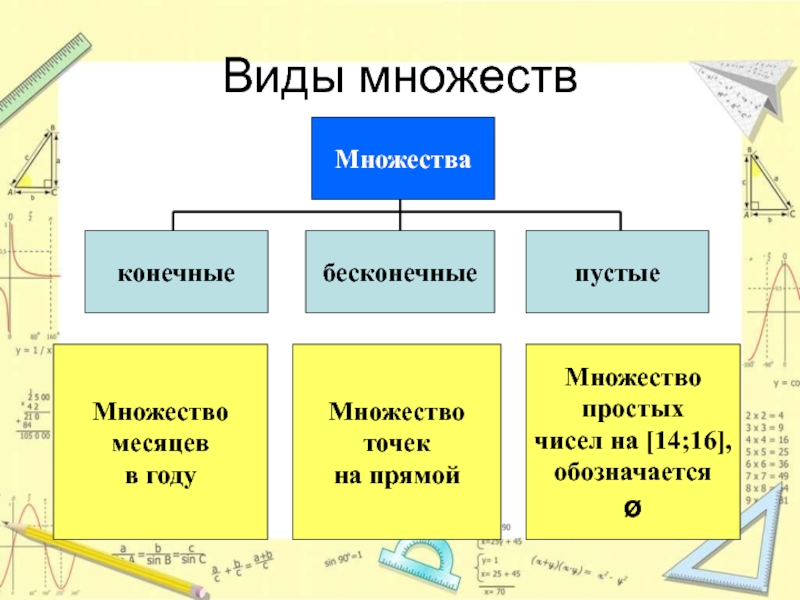
Множество комплексных чисел включает все числа вида a + bi, где a и b — действительные числа, а i — мнимая единица, такая как √-1.

Множество действительных чисел охватывает все числа, которые можно изобразить на числовой прямой, включая как рациональные, так и иррациональные числа.

Множество вещественных чисел – это объединение рациональных и иррациональных чисел, играющее ключевую роль в анализе и других областях математики.

Не забывайте о понятии кардинальности множества: множества, такие как натуральные числа и вещественные числа, имеют разные уровни бесконечности.