Советы по использованию и анализу пар перпендикулярных отрезков для начинающих и профессионалов
Пары перпендикулярных отрезков — важная концепция в геометрии, применяемая во многих областях математики и инженерии. На этой странице представлены полезные советы и примеры для более глубокого понимания и использования этих объектов в различных задачах.
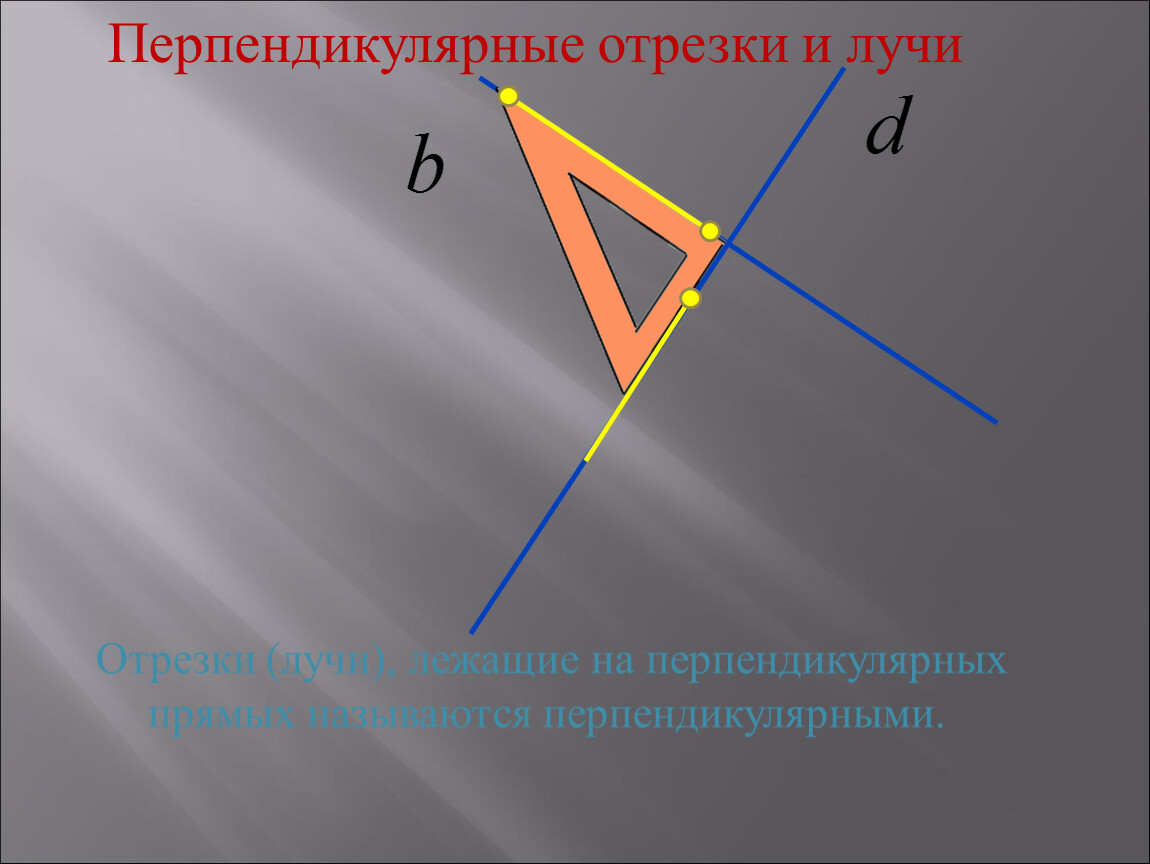

При анализе перпендикулярных отрезков важно помнить, что их длина не влияет на углы между ними, которые всегда составляют 90 градусов.

Параллельные прямые - Математика - TutorOnline
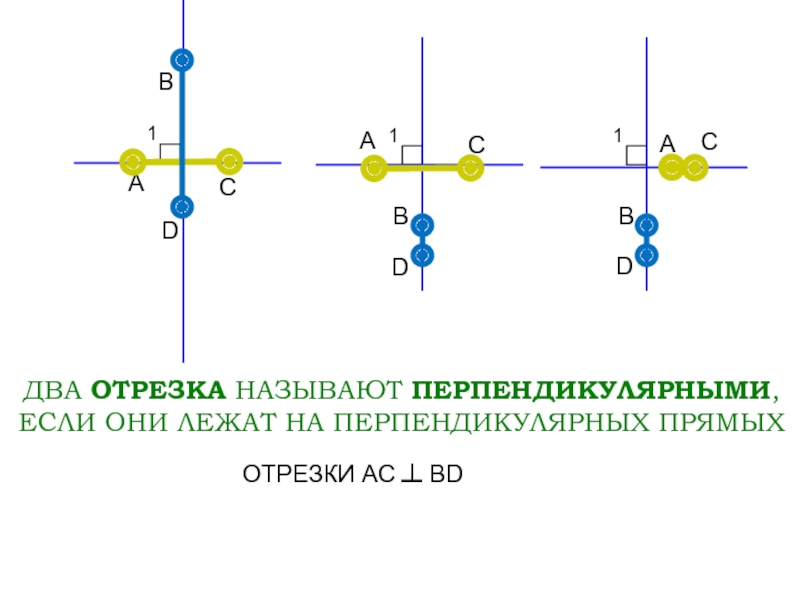
Для вычисления углов между двумя перпендикулярными отрезками используйте теорему о прямоугольном треугольнике, чтобы найти другие параметры, такие как гипотенуза или катеты.

2 урок геометрии. Откладывание отрезков и углов.
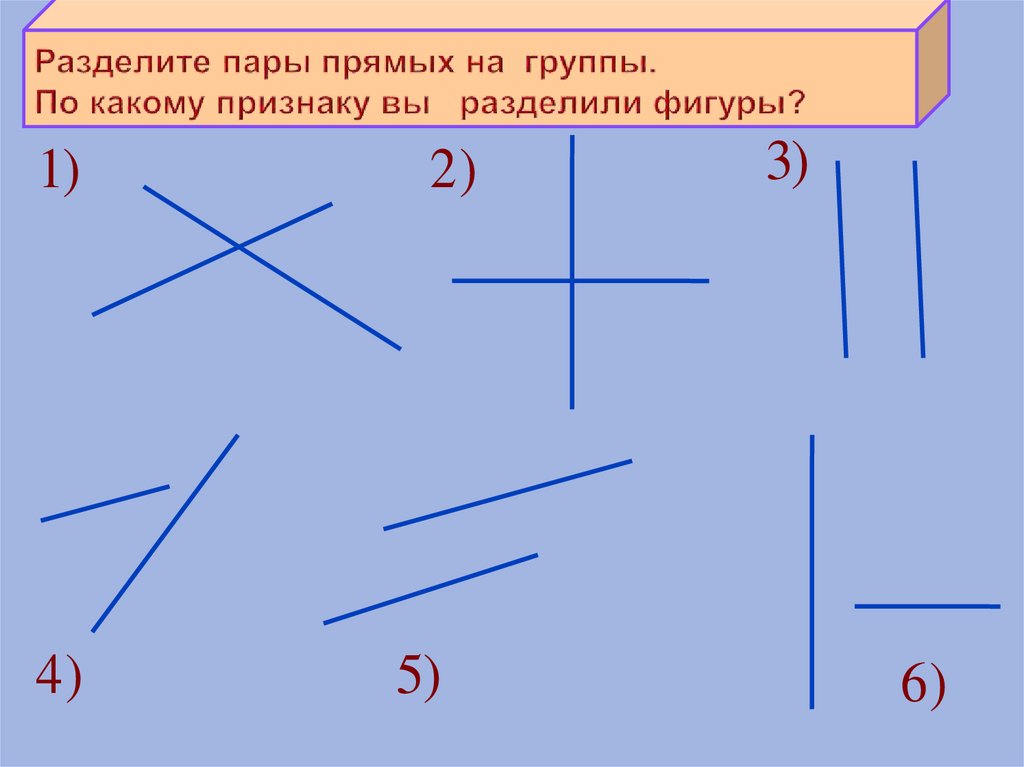
При построении фигур с перпендикулярными отрезками всегда проверяйте правильность углов с помощью транспортира или других геометрических инструментов.

8 класс, 36 урок, Свойства серединного перпендикуляра к отрезку
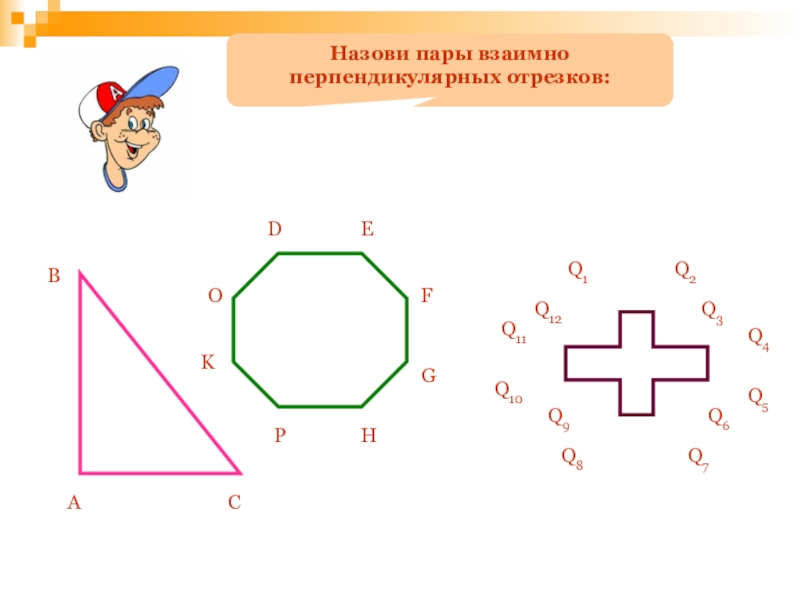
Используйте координатную плоскость для определения перпендикулярности отрезков, проверив, что скалярное произведение их направляющих векторов равно нулю.

Перпендикулярные прямые. 6 класс.
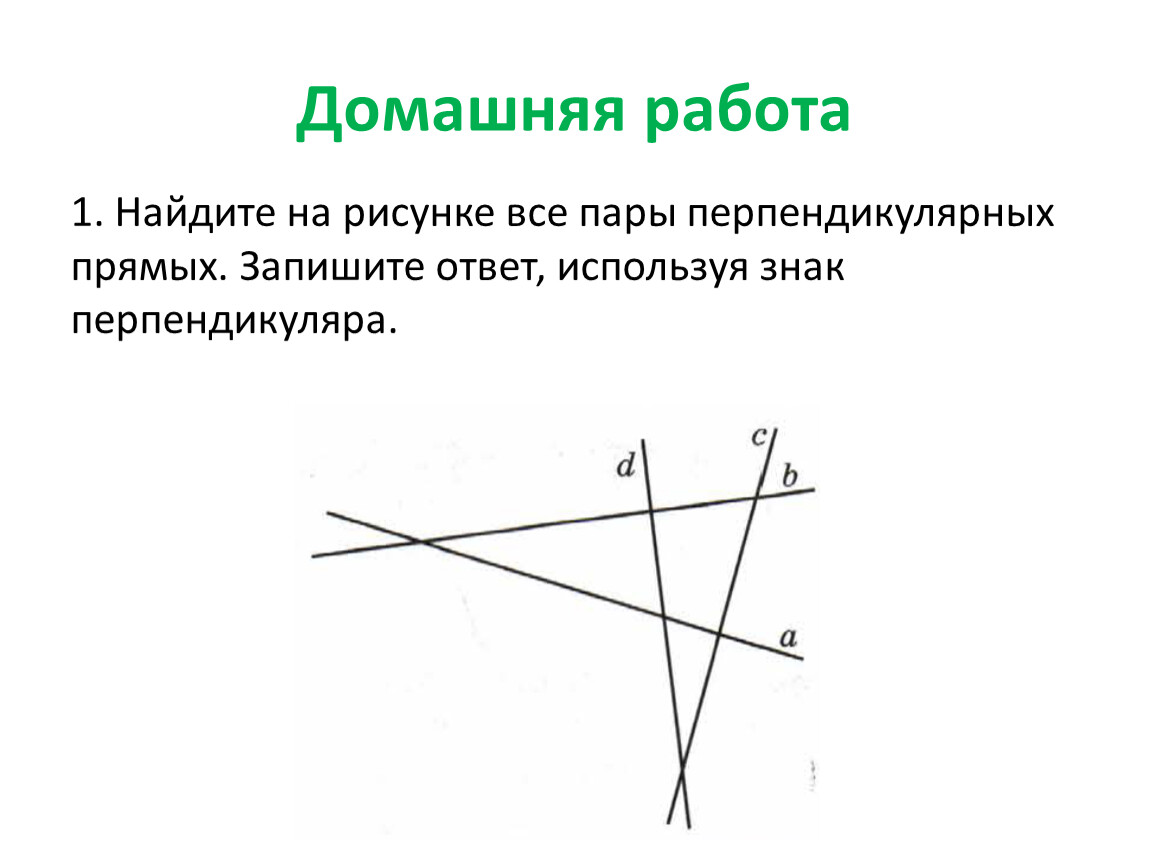
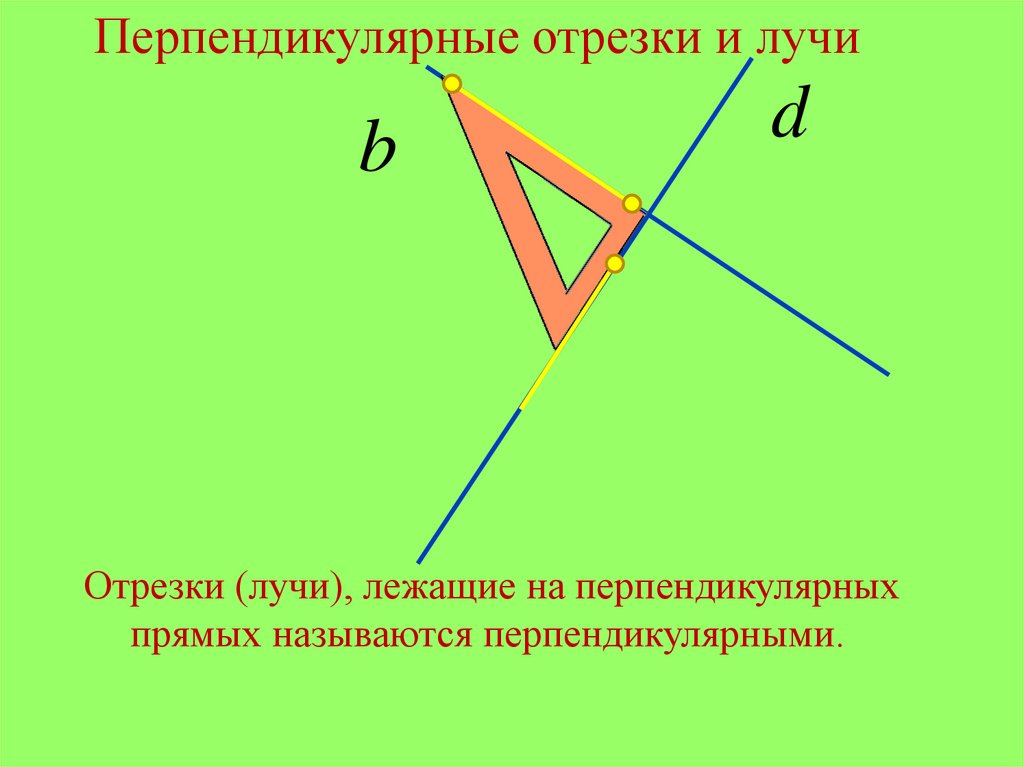
При решении задач на нахождение перпендикулярных отрезков важно внимательно учитывать условия задачи, такие как расположение точек и прямых.

урок№98 Перпендикулярные прямые и отрезки 6 класс

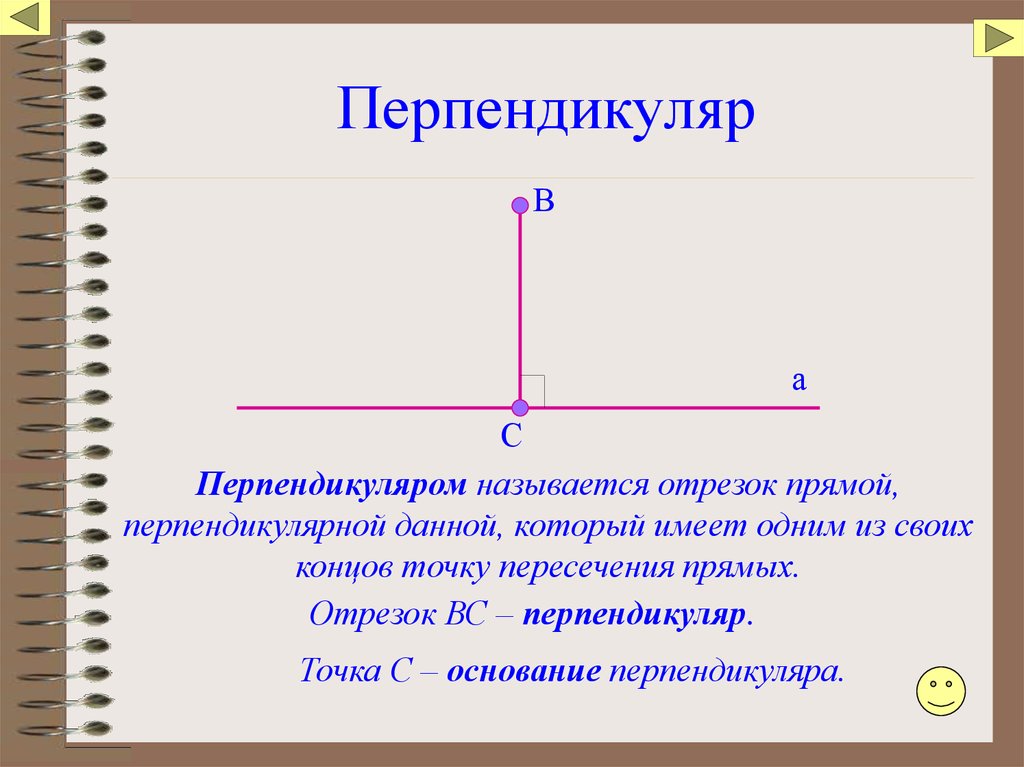
Когда работаете с перпендикулярными отрезками в пространстве, применяйте методы векторной алгебры для упрощения расчетов и доказательств.

8 класс, 19 урок, Пропорциональные отрезки
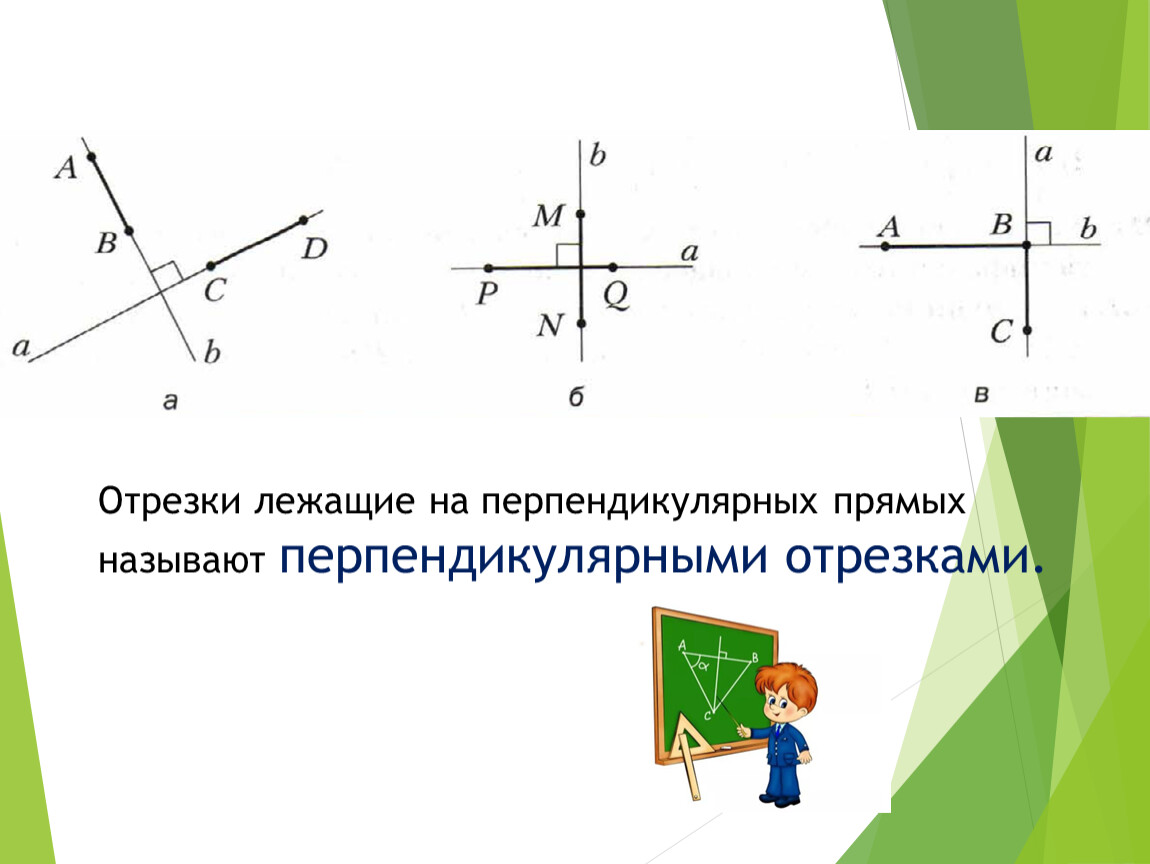
Для построения перпендикулярных отрезков с заданной длиной можно использовать циркуль или линейку, чтобы строго соблюдать пропорции.
Не забывайте, что два отрезка, перпендикулярные друг другу, могут служить основой для построения множества других геометрических объектов, таких как прямоугольники или квадраты.

Перпендикулярность прямой и плоскости. 10 класс.
Для проверки, что отрезки действительно перпендикулярны, можно использовать теорему Пифагора в прямоугольном треугольнике, образованном этими отрезками.

В задачах на перпендикулярные отрезки важно учитывать, что они могут быть частью более сложных геометрических фигур, таких как параллелограммы, прямоугольники или трапеции.
