Практическое применение параметрических уравнений для анализа траекторий
На этой странице вы найдете подборку фотографий и полезные советы о том, как использовать параметрические уравнения для описания и анализа траекторий движения. Мы расскажем о принципах работы с такими уравнениями и дадим практические рекомендации для их успешного применения.
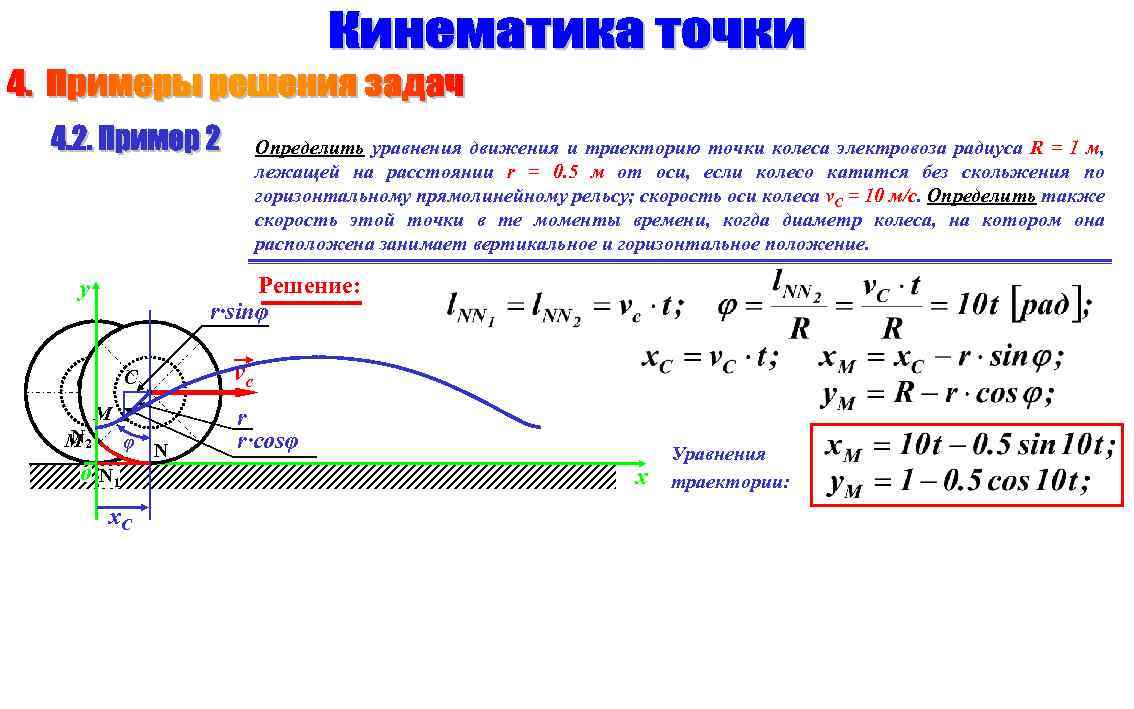

Начните с изучения основных формул параметрических уравнений: например, уравнений для определения положения объекта по времени.
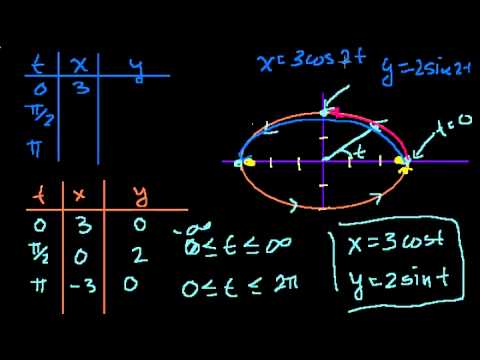
Параметрические уравнения (часть 4)


Используйте программное обеспечение, такое как MATLAB или Python, для визуализации траекторий на графиках.

Видеоурок \
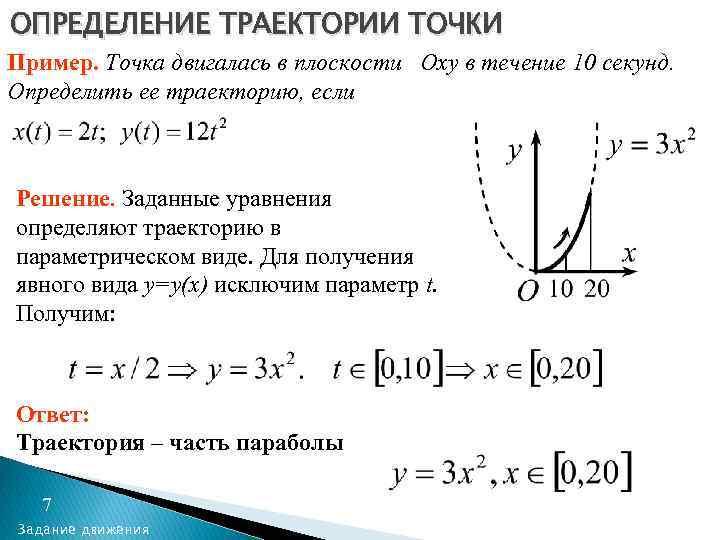
Проверяйте корректность введенных данных, чтобы избежать ошибок при построении графиков.

Параметрическое уравнение прямой 3 октября 2022 г.
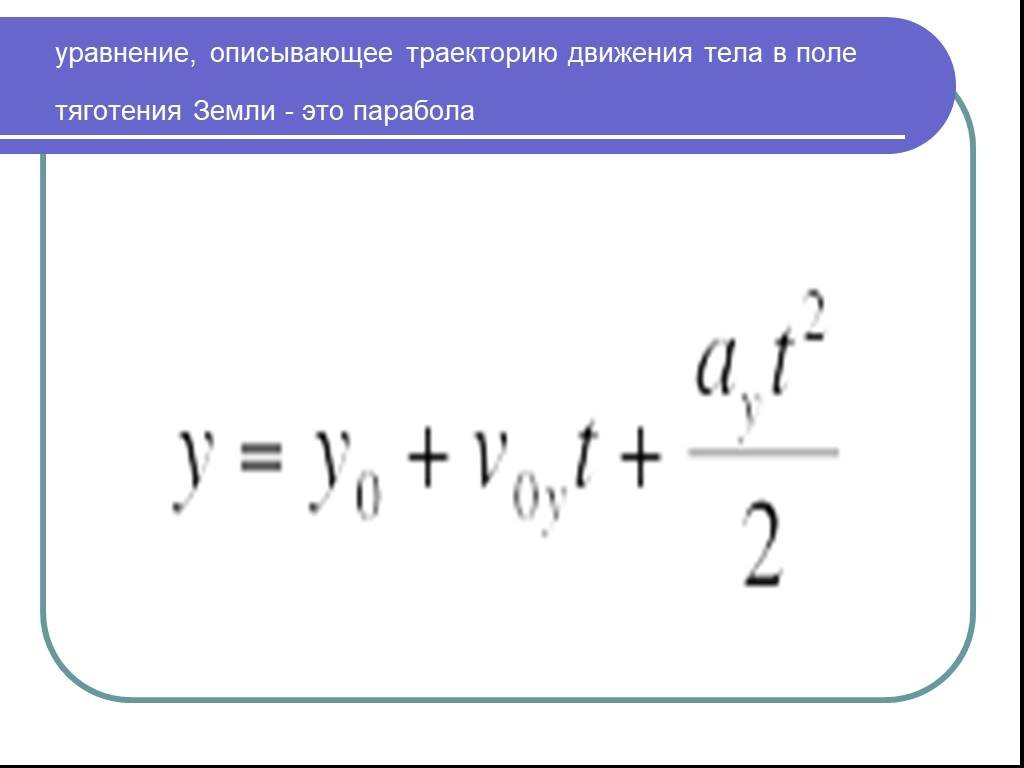
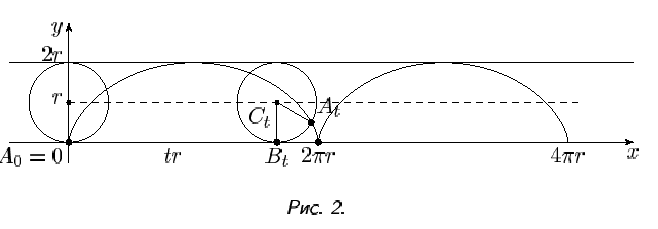
Экспериментируйте с различными параметрами, чтобы понять, как они влияют на форму траектории.
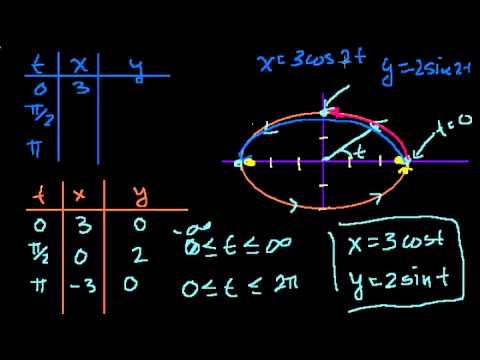
Параметрические уравнения (часть 4)

Применяйте параметры реальных объектов (масса, начальная скорость, угол) для моделирования траекторий в задачах физики.

Параметрические уравнения (часть 3)
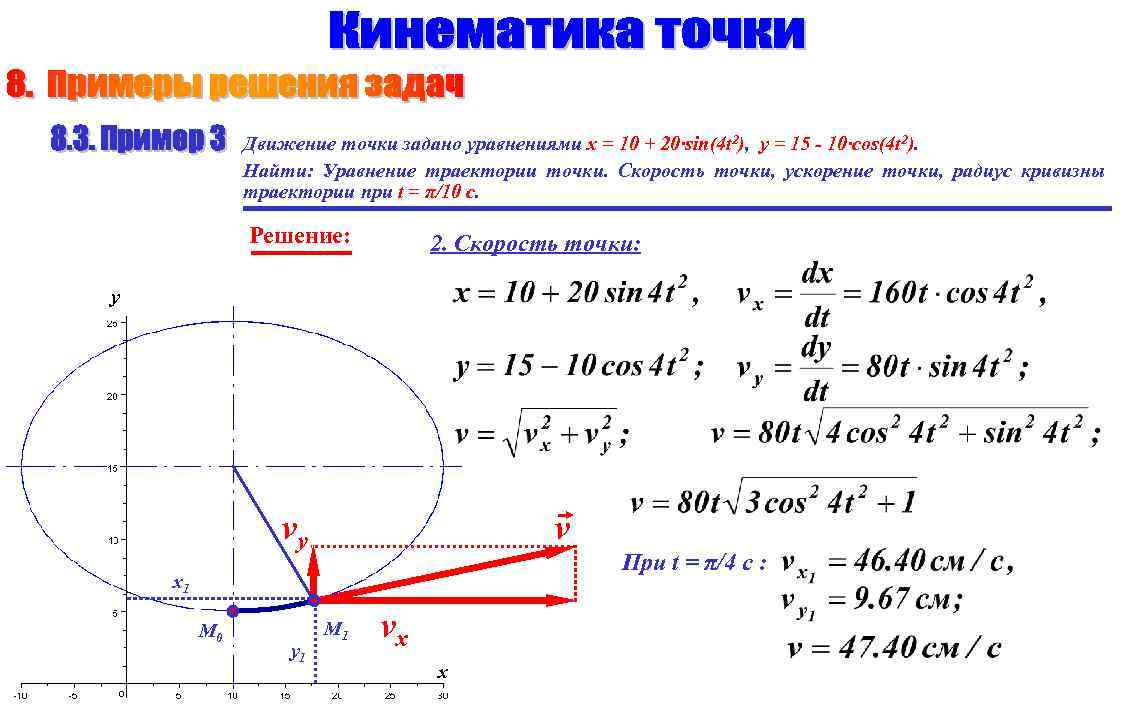
Изучайте классические примеры, такие как движение по параболе или окружности, чтобы лучше понять общие принципы.

Траектория и уравнения движения точки. Задача 1
Используйте аналитические методы для нахождения ключевых точек траектории, таких как вершины или точки пересечения.
Добавляйте ограничения в уравнения, если траектория должна учитывать реальные условия, например, гравитацию или сопротивление воздуха.

1 серия \
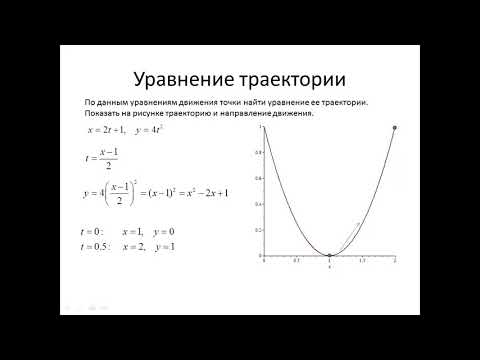
Теоретическая механика 2020 - Практика 1. Кинематика точки.


Работайте с параметрами времени и расстояния для создания анимаций движения.
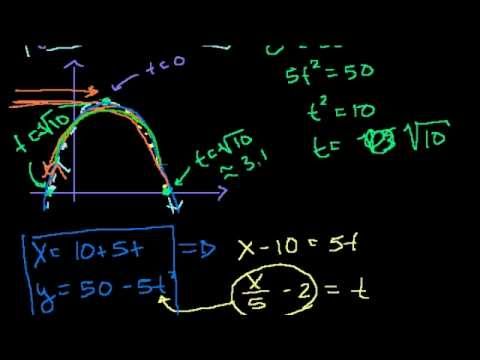
Параметрические уравнения (часть 2)


Проводите сравнение между теоретическими расчетами и экспериментальными данными для проверки точности модели.

Лекция 5.3 - Уравнение траектории - Александр Чирцов - Лекториум
