Как строить и интерпретировать фигуры Лиссажу с помощью параметрических уравнений

Фигуры Лиссажу представляют собой замкнутые кривые, которые получаются при наложении синусоидальных колебаний в двух перпендикулярных направлениях. Они используются для визуализации сложных периодических движений и могут быть построены с помощью параметрических уравнений. В данной статье вы найдете советы и рекомендации по построению таких фигур, а также примеры их применения в различных областях, от математического моделирования до искусства.

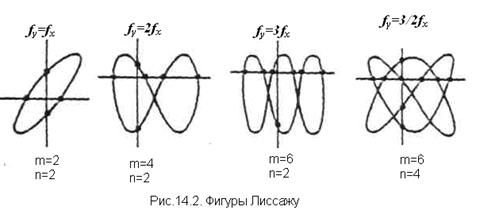
Для построения фигур Лиссажу используйте два синусоидальных уравнения для каждой из осей координат: x = A * sin(ω₁t + φ₁), y = B * sin(ω₂t + φ₂), где A и B — амплитуды, ω₁ и ω₂ — угловые частоты, а φ₁ и φ₂ — фазы.

При изменении соотношения амплитуд A и B вы можете изменять форму получаемой фигуры: когда амплитуды равны, получается круг, а когда одно значение значительно больше другого — эллипс или более сложные формы.

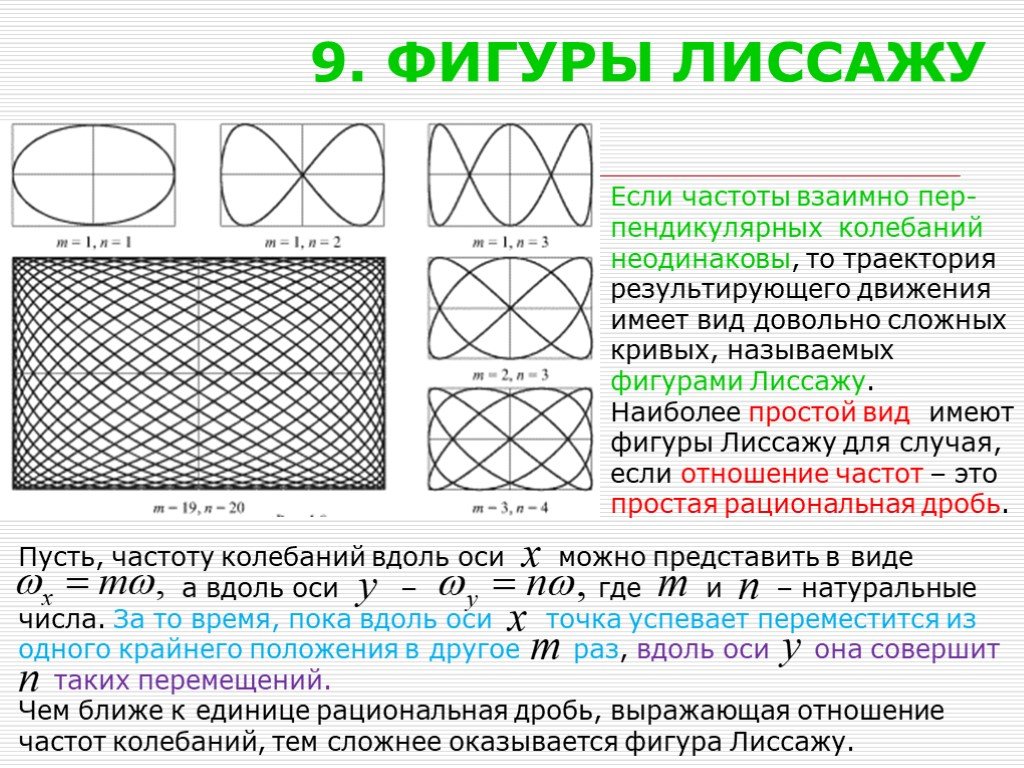
Если угловые частоты ω₁ и ω₂ не совпадают, то фигуры Лиссажу будут более сложными и могут создавать эффект петли или скручивания, в зависимости от соотношения этих частот.

Фазы φ₁ и φ₂ могут влиять на ориентацию и расположение фигуры на плоскости. Изменяя фазы, можно добиться различных эффектов, таких как вращение фигуры или изменение ее симметрии.

Для создания более сложных фигур Лиссажу можно использовать дополнительные гармоники или более сложные уравнения, добавляя новые компоненты в каждое из направлений.

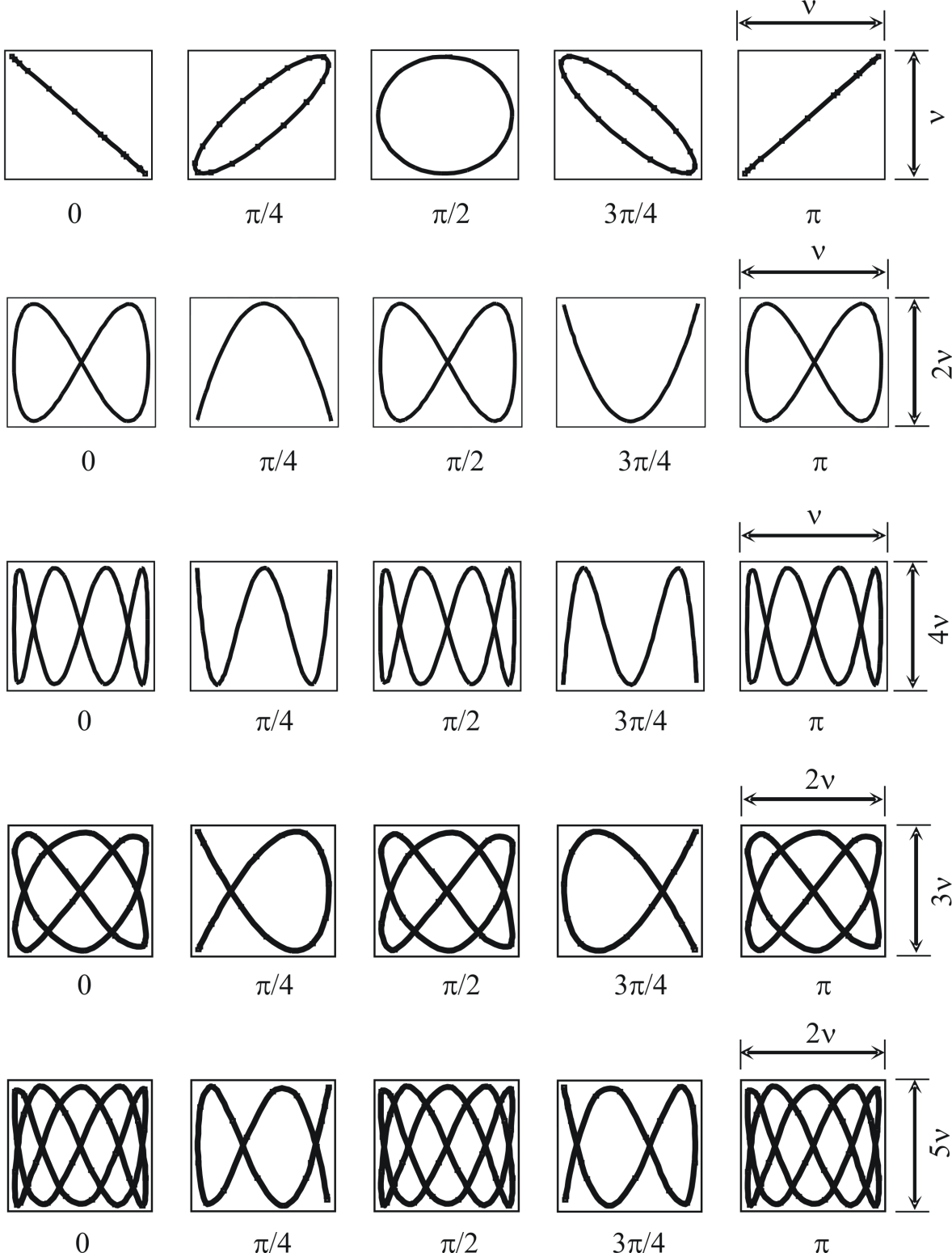
Используйте параметры уравнений для точной настройки рисунка: малые изменения в значениях частот или амплитуд могут существенно изменить внешний вид фигуры.

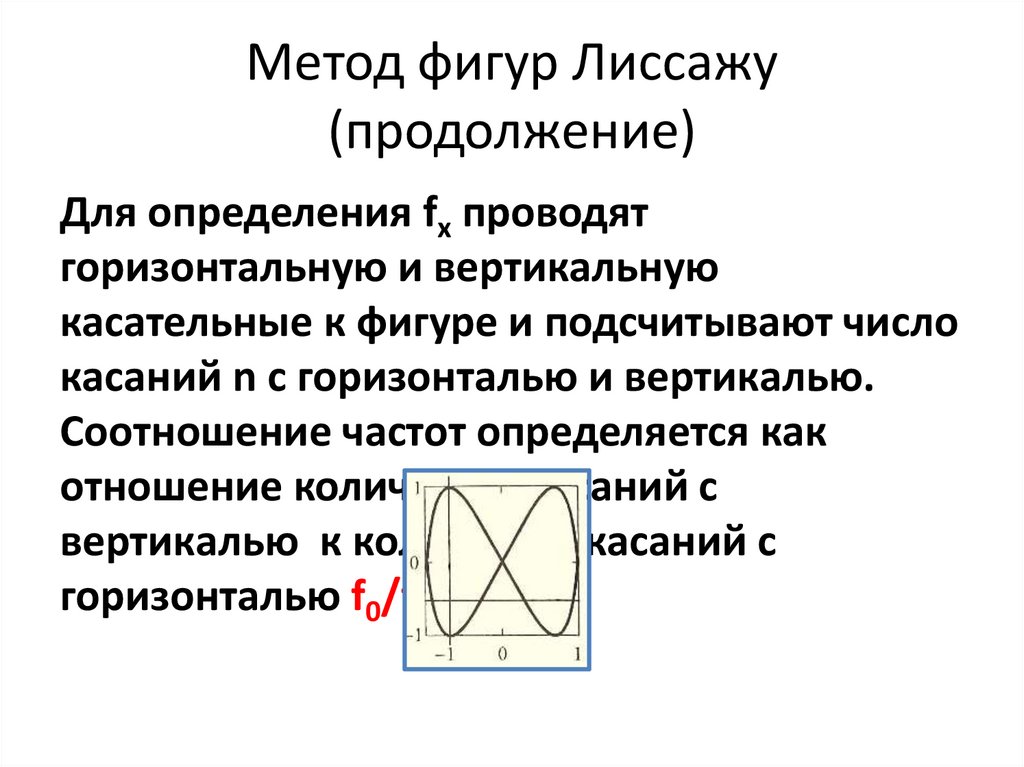
Попробуйте визуализировать фигуры Лиссажу с использованием программных средств, таких как Python (с использованием библиотеки Matplotlib) или MATLAB, для более детального анализа и моделирования.

Помимо математических приложений, фигуры Лиссажу могут использоваться для создания художественных изображений, например, в генеративном искусстве или в дизайне, где важна сложность и эстетика формы.

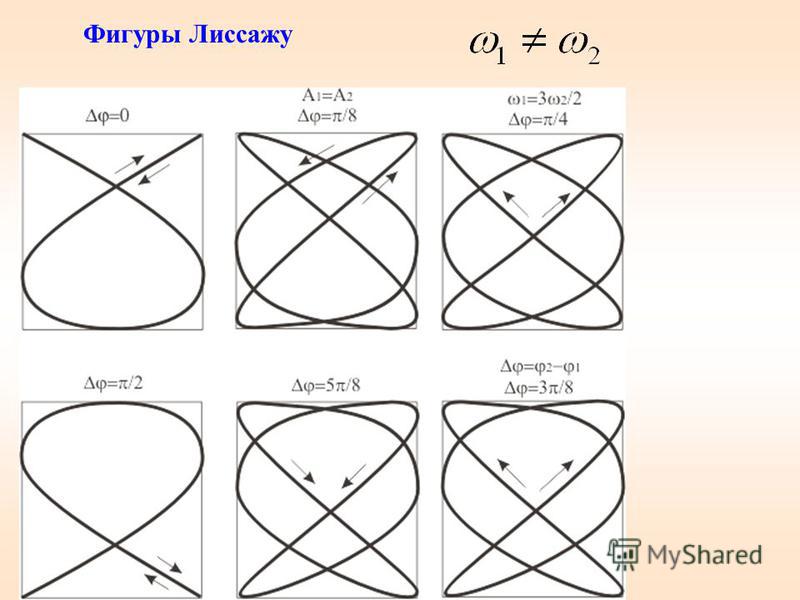
Обратите внимание на фазовые сдвиги между компонентами уравнений — они могут существенно изменить характер движения и образующиеся траектории.

Если хотите получить непрерывные и более плавные фигуры, используйте одинаковые или близкие значения для угловых частот ω₁ и ω₂, избегая резких изменений и переломов в форме.