Параллелограммы на чертежах: как решать задачи эффективно и быстро
На этой странице вы найдете полезные советы по решению задач с параллелограммами, представленных на готовых чертежах. Мы разберем основные подходы, особенности геометрии параллелограмма и различные методы вычислений, которые помогут вам успешно справиться с такими задачами. Применяя эти рекомендации, вы сможете ускорить процесс решения и повысить точность своих ответов.
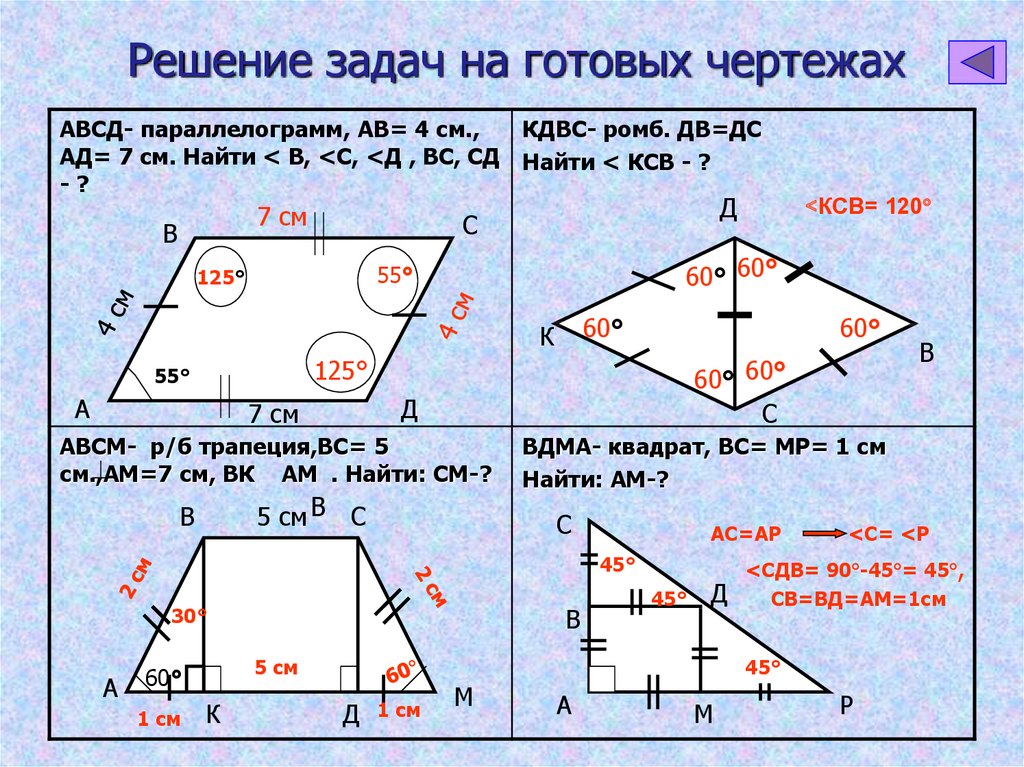
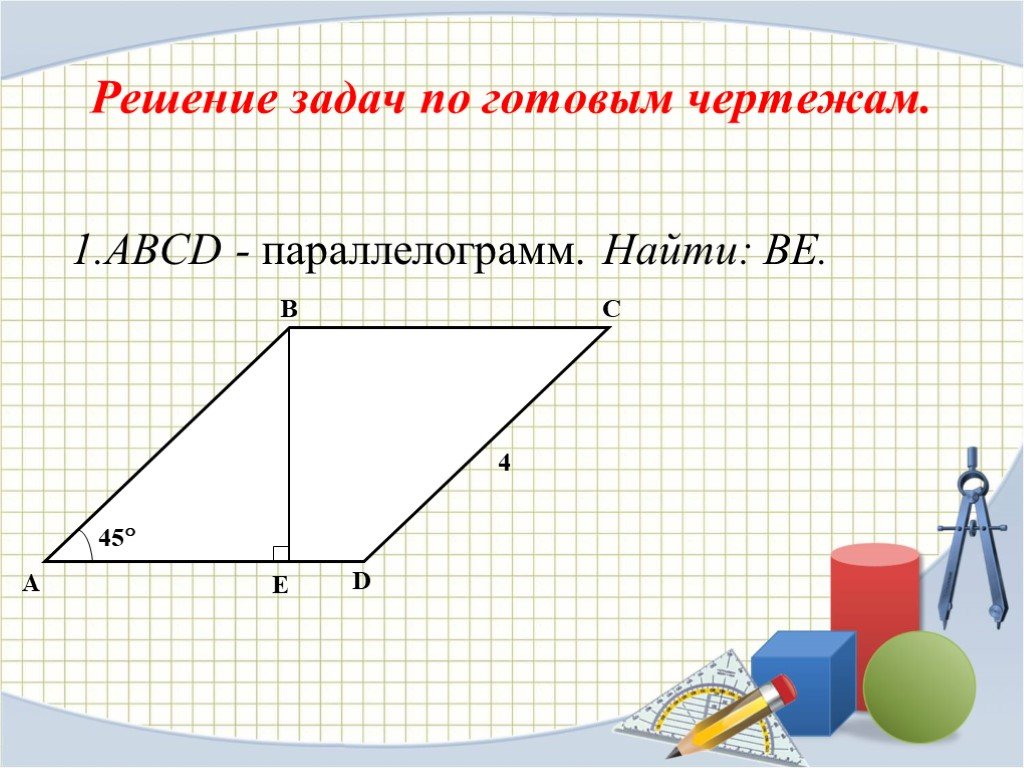

Для решения задач на параллелограммы используйте свойства фигур, такие как параллельность противоположных сторон и равенство углов.

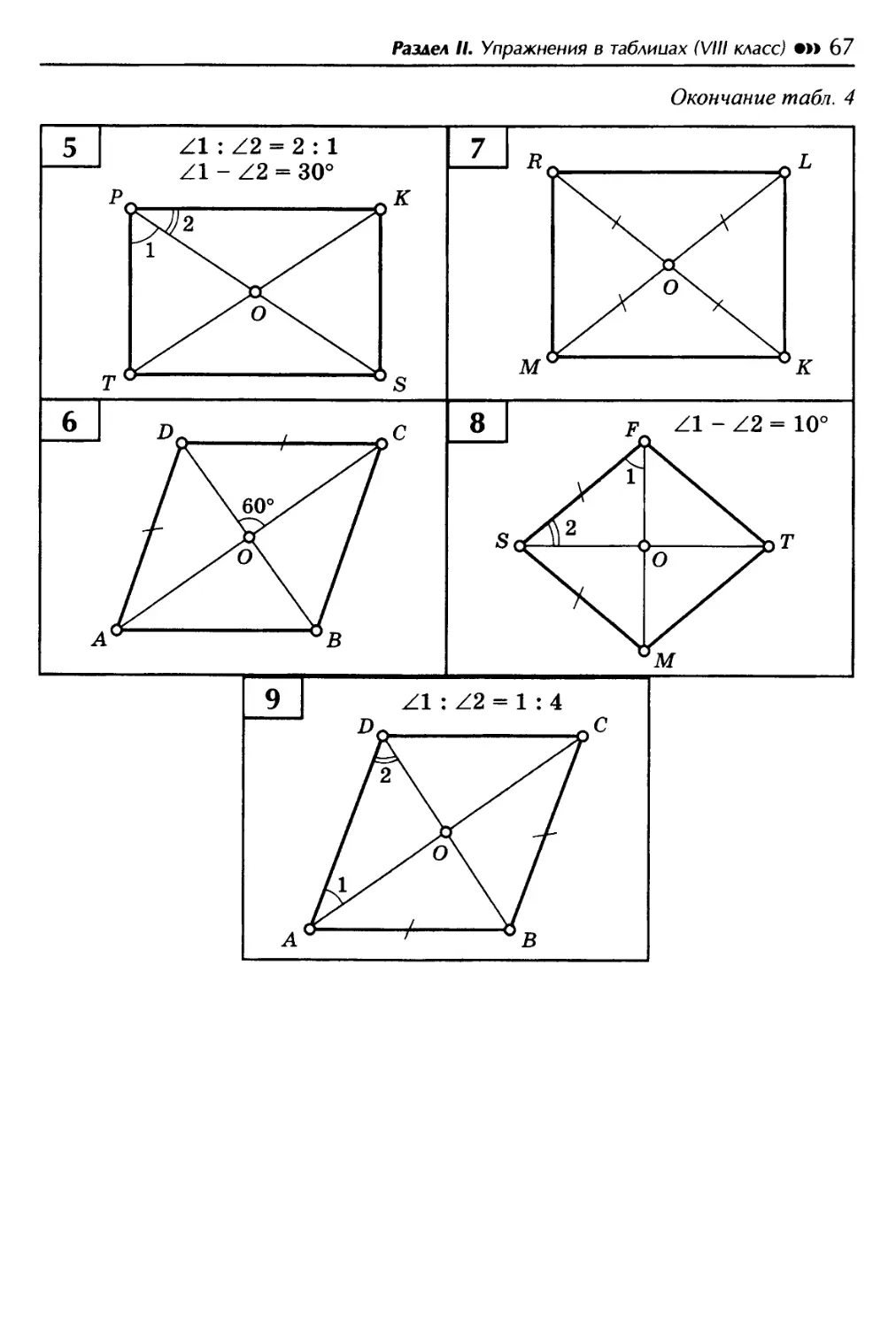
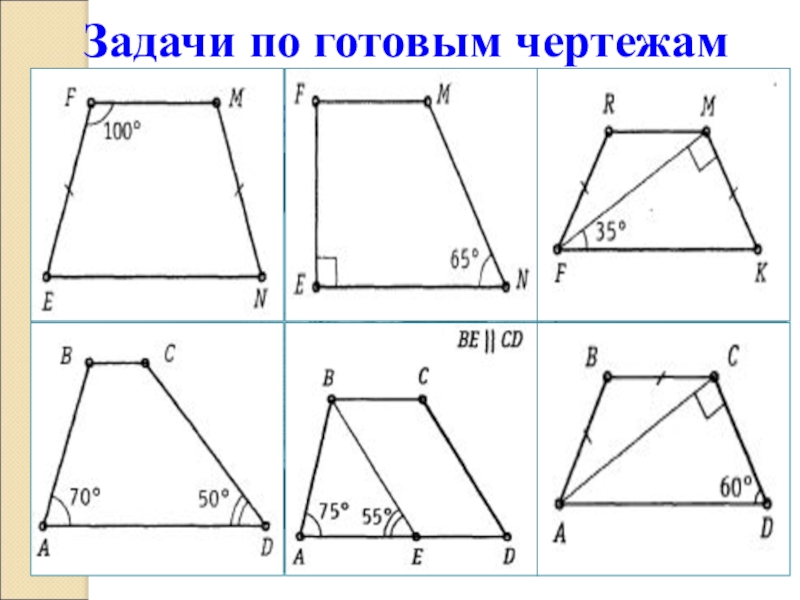
Параллелограмм. Задачи на готовых чертежах. Найдите неизвестные углы №№ 1, 2.


Обратите внимание на чертежи: часто дополнительная информация о длине сторон или углах помогает быстрее найти решение.
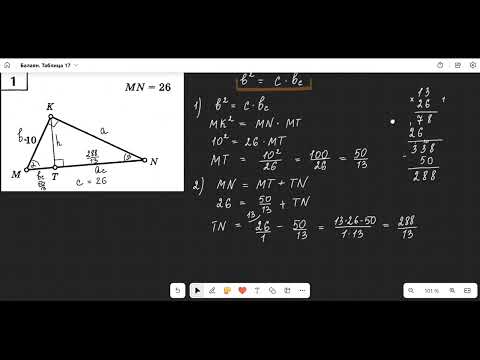
1️⃣ ЗАДАЧИ НА ГОТОВЫХ ЧЕРТЕЖАХ БАЛАЯН
Если на чертеже указаны диагонали параллелограмма, попробуйте использовать их для нахождения углов или площади.

Параллелограмм. Практическая часть - решение задачи. 8 класс.

Помните, что для нахождения площади параллелограмма можно использовать формулу S = a * h, где a — основание, а h — высота.

Балаян 7-9. Геометрия. Параллелограмм. стр 62.
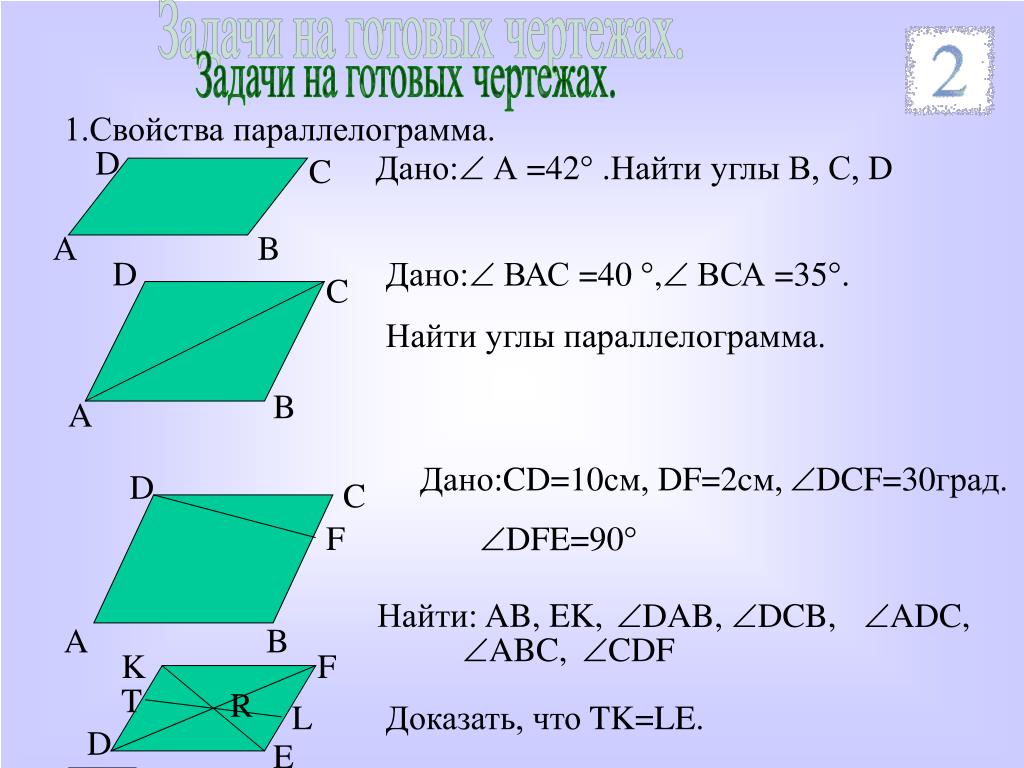
Не забывайте проверять, что на чертеже правильно обозначены все элементы: углы, стороны и высоты. Ошибки в обозначениях могут привести к неверным результатам.

Параллелограмм. Задачи на готовых чертежах. Найдите неизвестные углы №№ 4 и 5.

Для анализа углов параллелограмма используйте теорему о том, что противоположные углы равны.
Если вам нужно найти периметр, вспомните, что периметр параллелограмма равен 2 * (a + b), где a и b — длины смежных сторон.

Геометрия 8. Параллелограмм. Практикум. Решение задач № 1 - 4
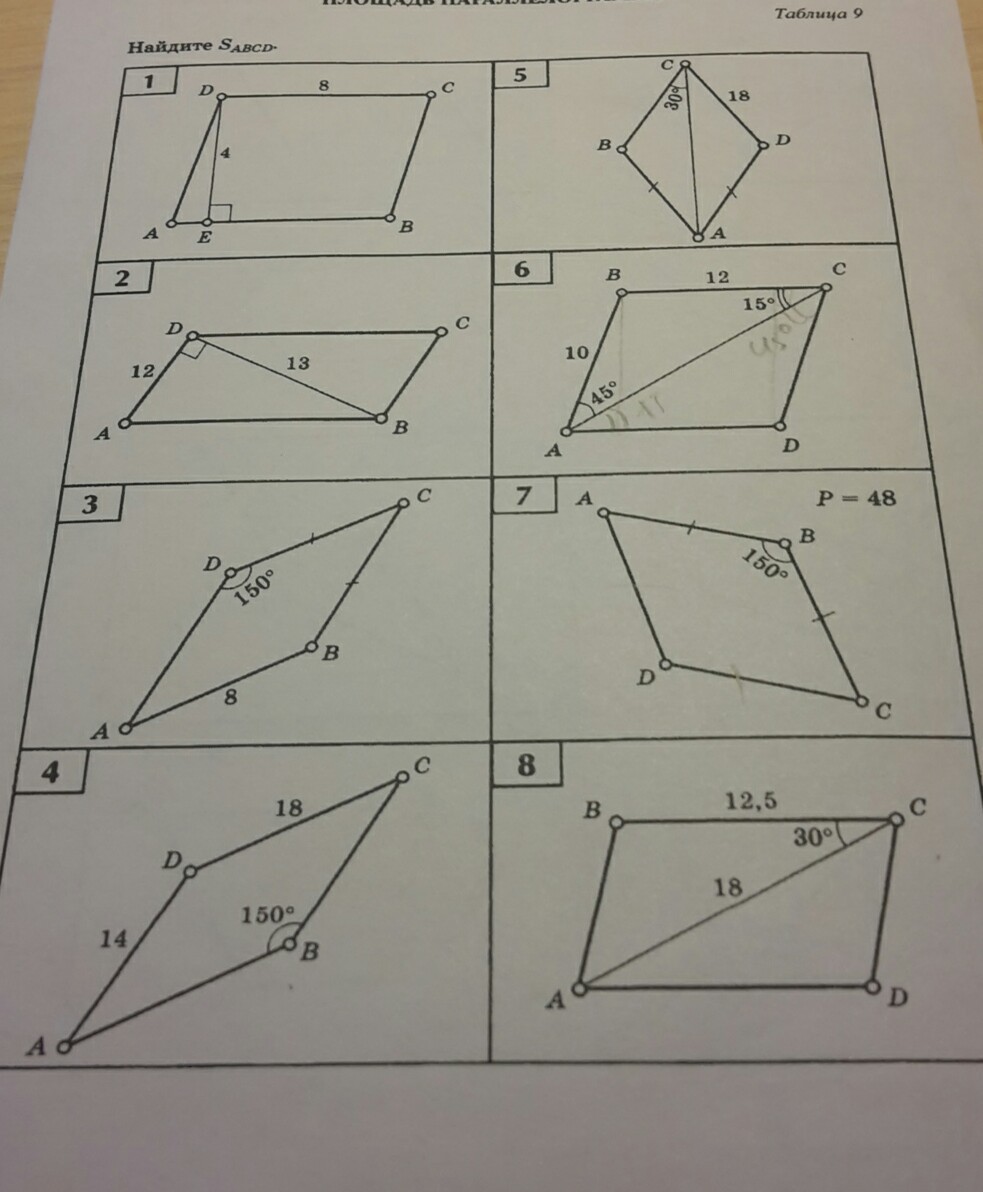
Когда задача требует нахождения диагонали, используйте теорему Пифагора для вычисления длины с учетом прямоугольных треугольников, образующихся при диагоналях.

Параллелограмм. Практическая часть - решение задачи. 8 класс.

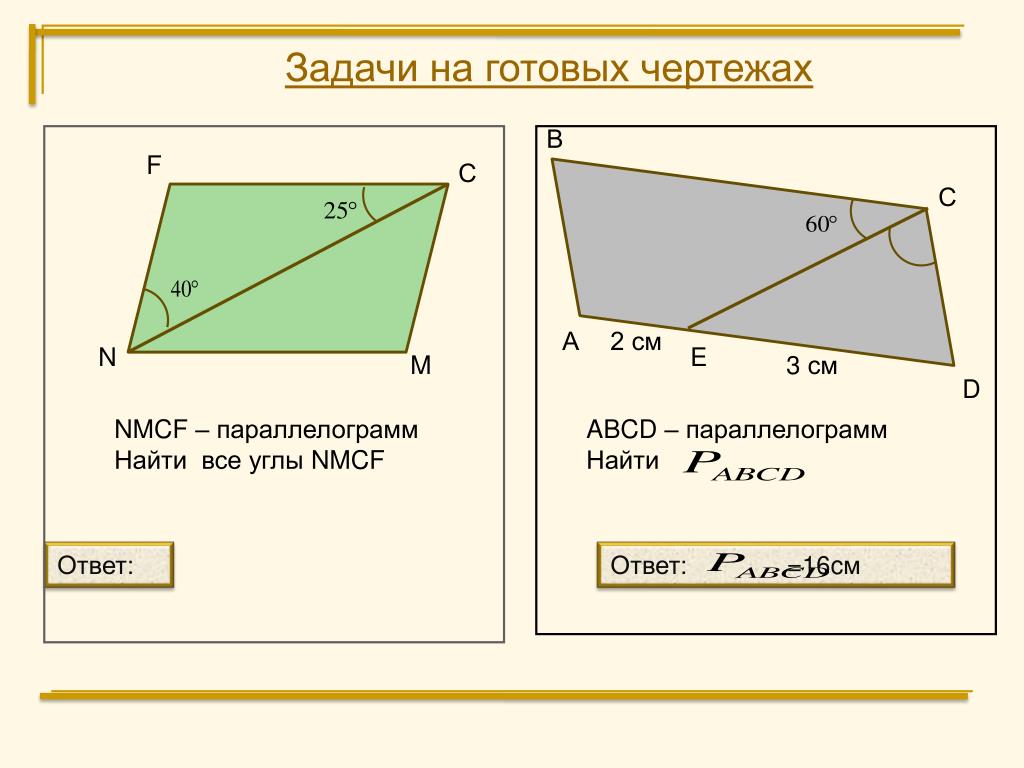
Если на чертеже указаны углы между диагоналями, то используйте их для поиска других углов и сторон параллелограмма.

Все про ПАРАЛЛЕЛОГРАММ за 8 минут: Свойства, Признаки, Формулы Периметра и Площади // Геометрия

Не стесняйтесь использовать различные методы, такие как проекций и векторов, если задача становится слишком сложной для стандартных методов решения.