Ключевые характеристики векторного произведения и его значение для анализа векторов
Векторное произведение — это операция, которая играет важную роль в различных областях науки, от физики до инженерии. Оно позволяет вычислять перпендикулярные векторы, определять площадь параллелограмма и другие геометрические характеристики, важные для решения задач с векторами. Знание основных свойств векторного произведения поможет вам глубже понять многие математические концепции и их практическое применение.


При вычислении векторного произведения всегда следите за правильным направлением полученного вектора — он будет перпендикулярным к плоскости, в которой лежат исходные векторы.

Математика без Ху%!ни. Смешанное произведение векторов


Для удобства запоминания порядка векторов при вычислении используйте правило правой руки: если пальцы правой руки направлены вдоль первого вектора, то большой палец укажет направление результата векторного произведения.

Математика без Ху%!ни. Свойства скалярного и векторного произведений.
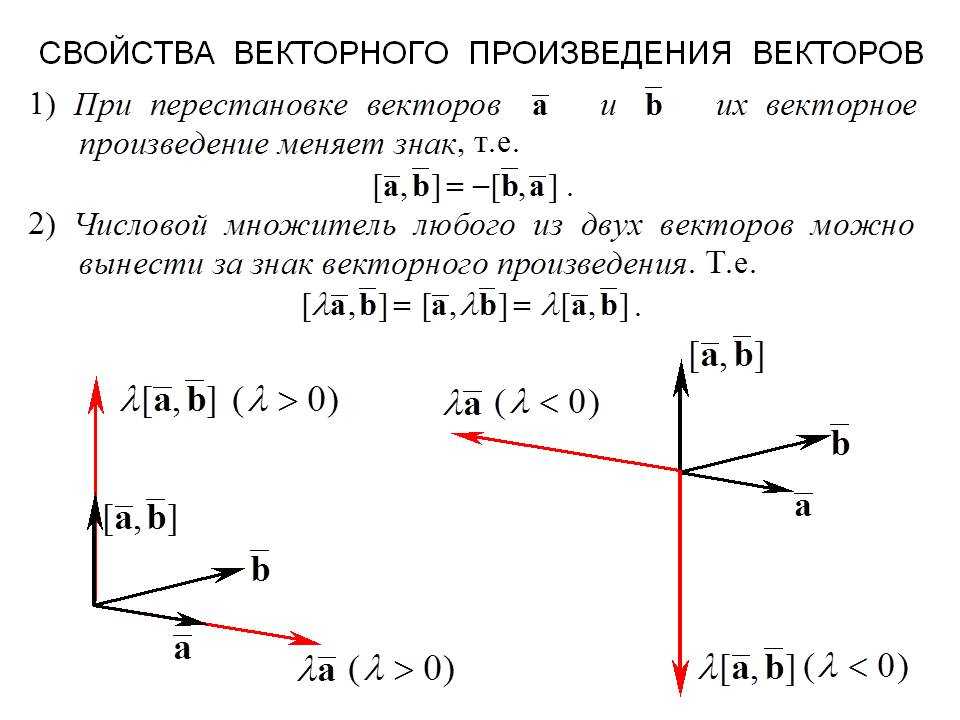
Помните, что векторное произведение не коммутативно, то есть порядок векторов имеет значение: a×b≠b×a/mathbf{a} /times /mathbf{b} /neq /mathbf{b} /times /mathbf{a}a×b=b×a, а результат отличается по направлению на 180 градусов.

Векторное произведение векторов


Векторное произведение всегда равно нулю, если два вектора коллинеарны, то есть лежат на одной прямой.

§13 Свойства векторного произведения
Используйте векторное произведение для нахождения площади параллелограмма, построенного на двух векторах — площадь равна модулю их векторного произведения.

Аналитическая геометрия, 3 урок, Векторное произведение


При вычислениях с векторным произведением всегда проверяйте, что векторы не являются нулевыми, иначе результат операции не будет определён.

Определение векторного произведения векторов

Если вам нужно вычислить векторное произведение в трёхмерном пространстве, используйте детерминант с координатами векторов для удобства вычислений.
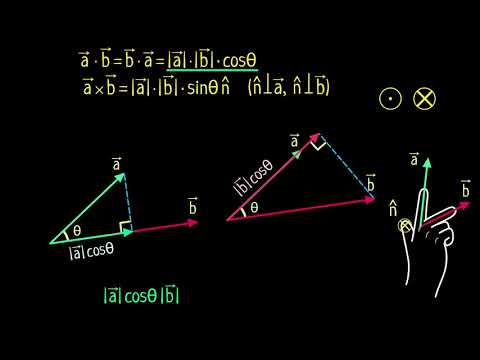
Сравнение скалярного и векторного произведений векторов (видео 16) - Магнетизм - Физика
Векторное произведение может быть полезно при вычислении моментов силы и углов между плоскостями или прямыми в механике и физике.
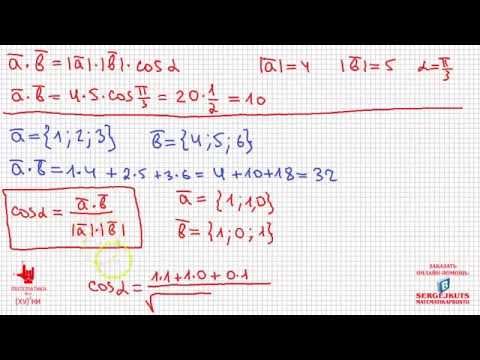
18+ Математика без Ху%!ни. Скалярное произведение векторов. Угол между векторами.

Вычисление векторного произведения векторов
Не забывайте, что для удобства использования векторного произведения часто применяют его свойства в контексте координатных систем и систем отсчёта.


Обратите внимание на то, что векторное произведение можно трактовать как операцию, которая помогает находить направление вращения или ориентацию объекта в пространстве.

18+ Математика без Ху%!ни. Векторное произведение.