Разбор понятия случайной величины и её роли в теории вероятностей
Случайная величина — это важное понятие в теории вероятностей и статистике, которое описывает числовое значение, которое может быть получено в результате случайного эксперимента. Различают дискретные и непрерывные случайные величины, и каждую из них характеризуют свои особенности. В этой статье мы разберем основные принципы и определения, связанные с случайными величинами, и предложим полезные советы для лучшего понимания этого фундаментального понятия.


При изучении случайных величин важно понимать разницу между дискретными и непрерывными величинами, так как это влияет на методы их анализа.

11. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ 📚 Теория вероятностей

Не забывайте, что для дискретных случайных величин часто используется таблица распределений вероятностей, а для непрерывных — функции плотности вероятности.

Математика без Ху%!ни. Ряд распределения дискретной случайной величины. Мат ожидание и дисперсия.

Для практического применения случайных величин полезно изучить математическое ожидание и дисперсию, так как эти параметры позволяют характеризовать основные свойства величины.

2 Определение случайной величины примеры - курс тервер до дыр на гребне волн


Понимание распределений случайных величин (например, нормальное, биномиальное, пуассоновское) поможет вам лучше интерпретировать результаты экспериментов и данных.

Прогноз на 2025 год от нумеролога Кристины Егиазаровой

Важно помнить, что случайная величина может быть описана как случайный процесс, что означает её зависимость от случайных факторов, влияющих на результат.

5000 лет назад: Наследие ануннаков, изменившее историю человечества

Для изучения случайных величин не забудьте ознакомиться с понятиями независимости и корреляции между различными величинами, которые играют ключевую роль в анализе данных.
Случайные величины. 10 класс.

Практическое применение случайных величин часто встречается в таких областях, как экономика, физика, инженерия и медицина, где важно учитывать случайные факторы в моделях.

A.4.4 Распределение случайной величины. Матожидание, дисперсия и их свойства.
При работе с случайными величинами важно учитывать вероятность возникновения экстремальных значений, так как это может существенно повлиять на результаты анализа.
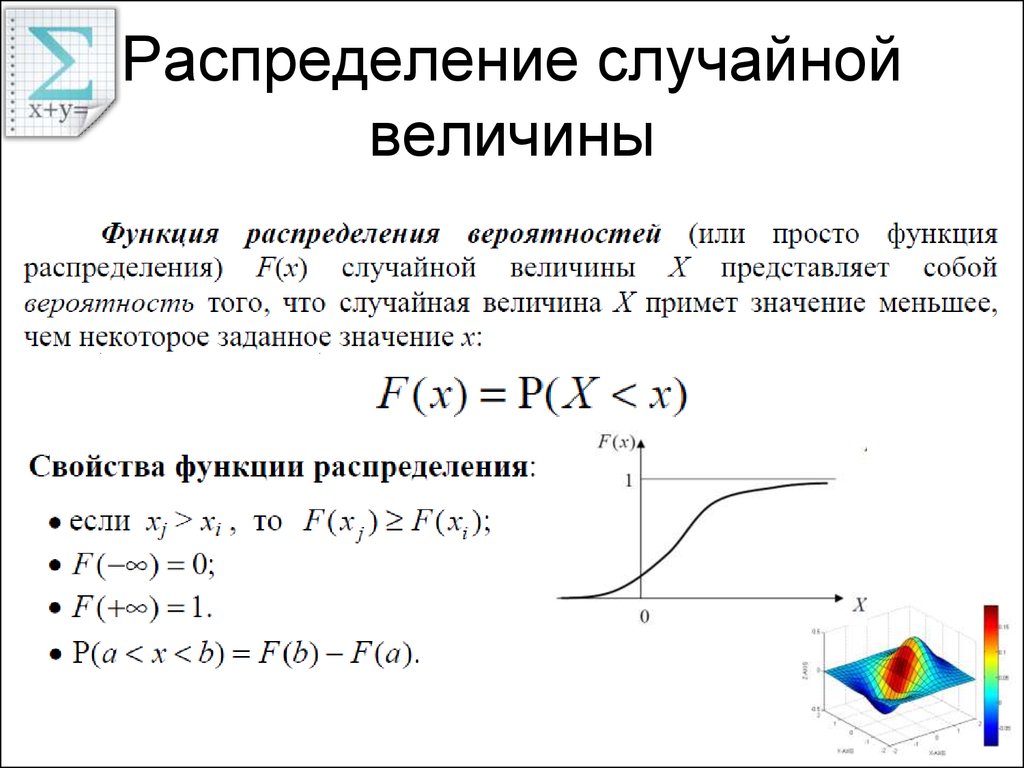

Используйте симуляции и статистические методы для проверки гипотез о случайных величинах, чтобы убедиться в корректности выбранной модели.


Не забывайте, что на практике случайные величины часто моделируются с помощью компьютерных алгоритмов, что позволяет эффективно анализировать большие объемы данных и находить скрытые закономерности.
