Как правильно работать с неориентированными планарными графами: советы и примеры
На этой странице представлены важные советы по работе с неориентированными планарными графами. Вы найдете полезную информацию о том, как лучше всего использовать этот тип графов в различных задачах, а также увидите примеры визуализаций, которые помогут лучше понять их структуру и особенности.
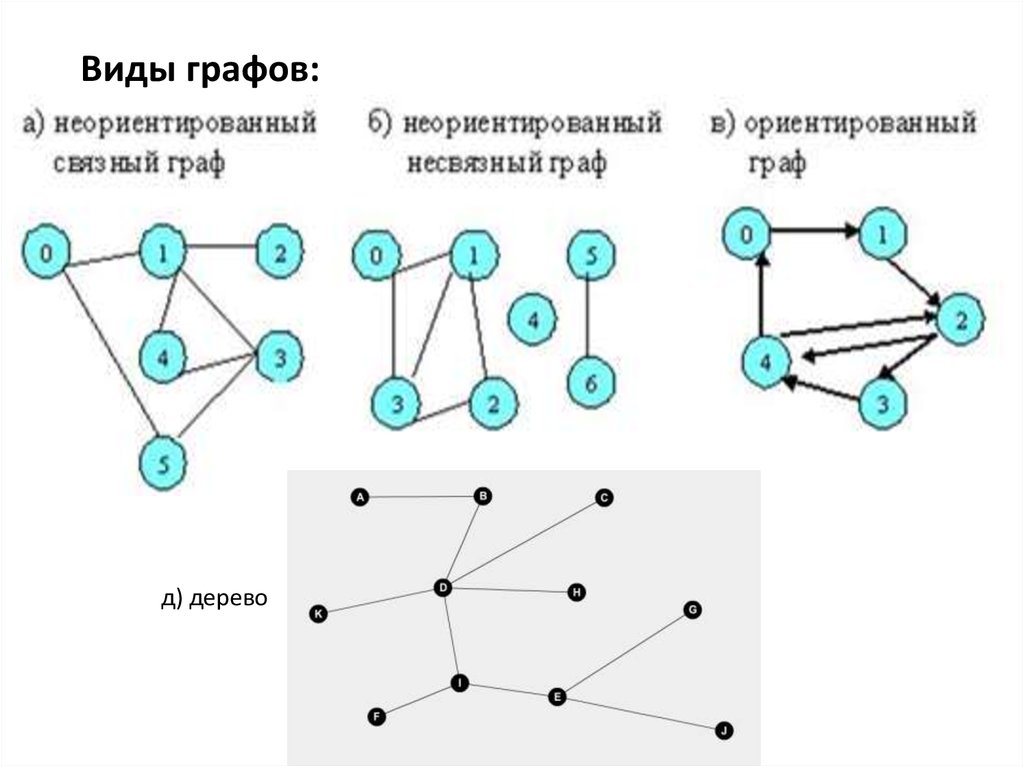
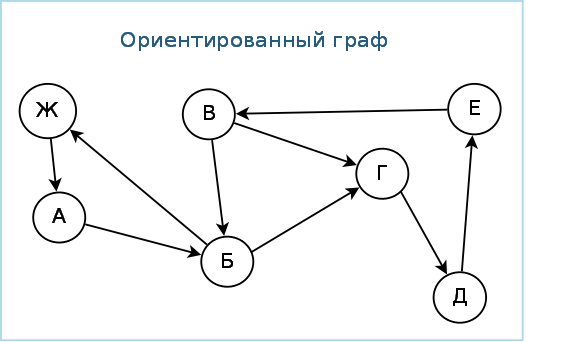
Перед тем как приступить к работе с неориентированными планарными графами, убедитесь, что вы четко понимаете основные характеристики таких графов, включая их возможные представления и важнейшие алгоритмы для обработки.

Что такое граф? - Дискретная математика - Умскул
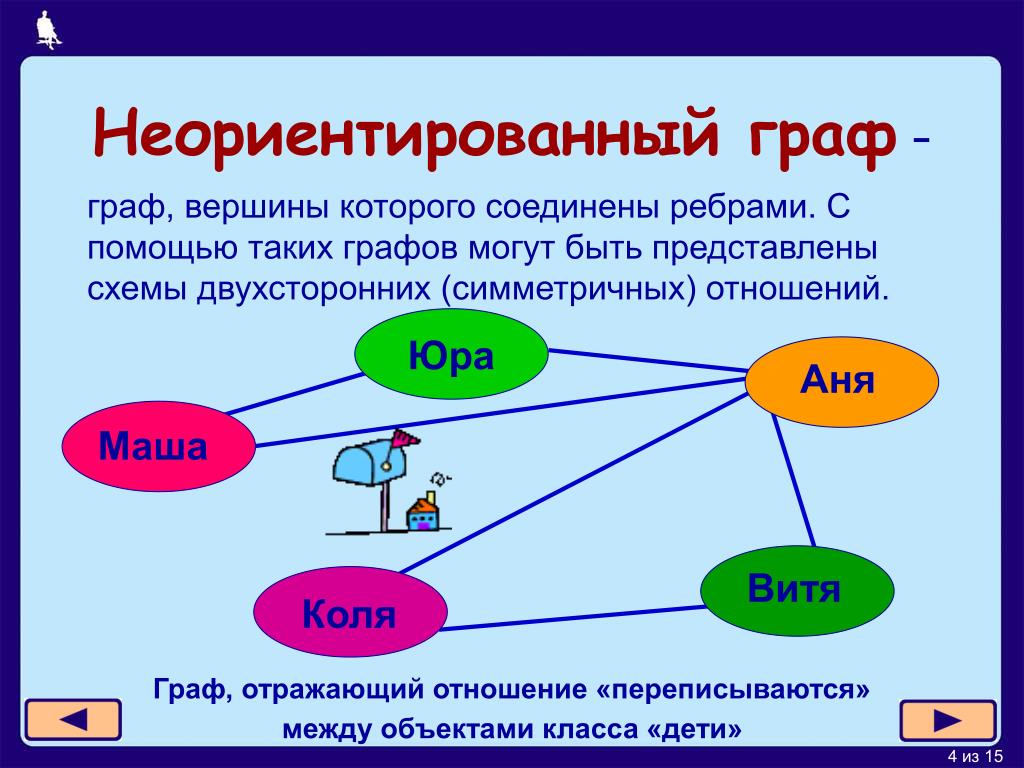
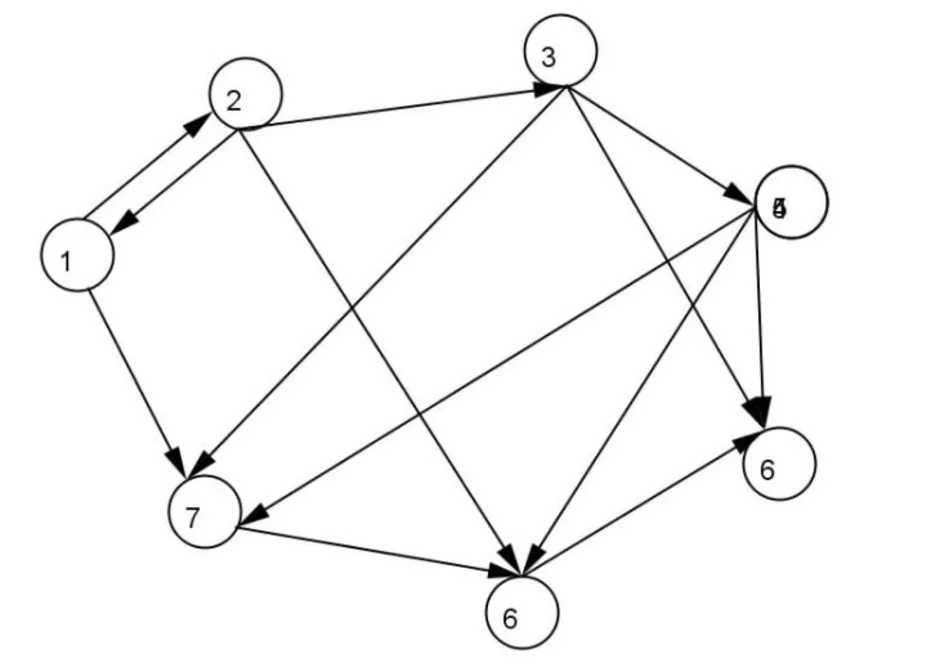
Для упрощения анализа планарных графов используйте визуализацию. Построение графов на плоскости с минимальными пересечениями рёбер позволит лучше увидеть их структуру и легко понять топологические особенности.

85 Двудольный ориентированный граф

При решении задач с планарными графами полезно обращать внимание на теорему Куранта–Фалкерсона, которая утверждает, что любой планарный граф можно нарисовать на плоскости так, чтобы его рёбра не пересекались.
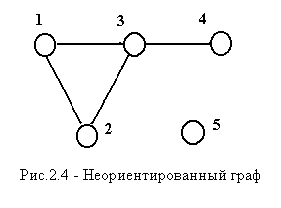
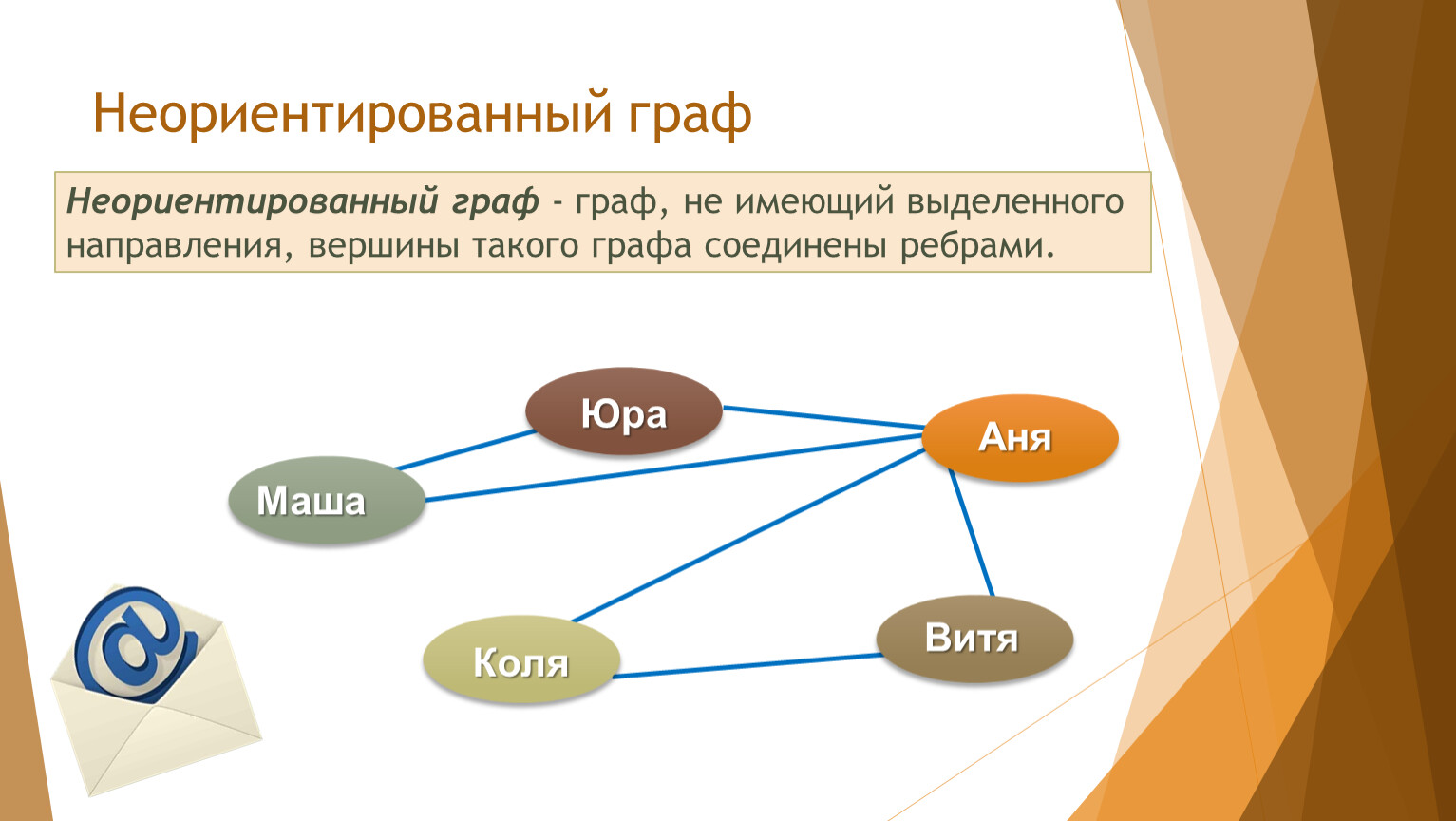
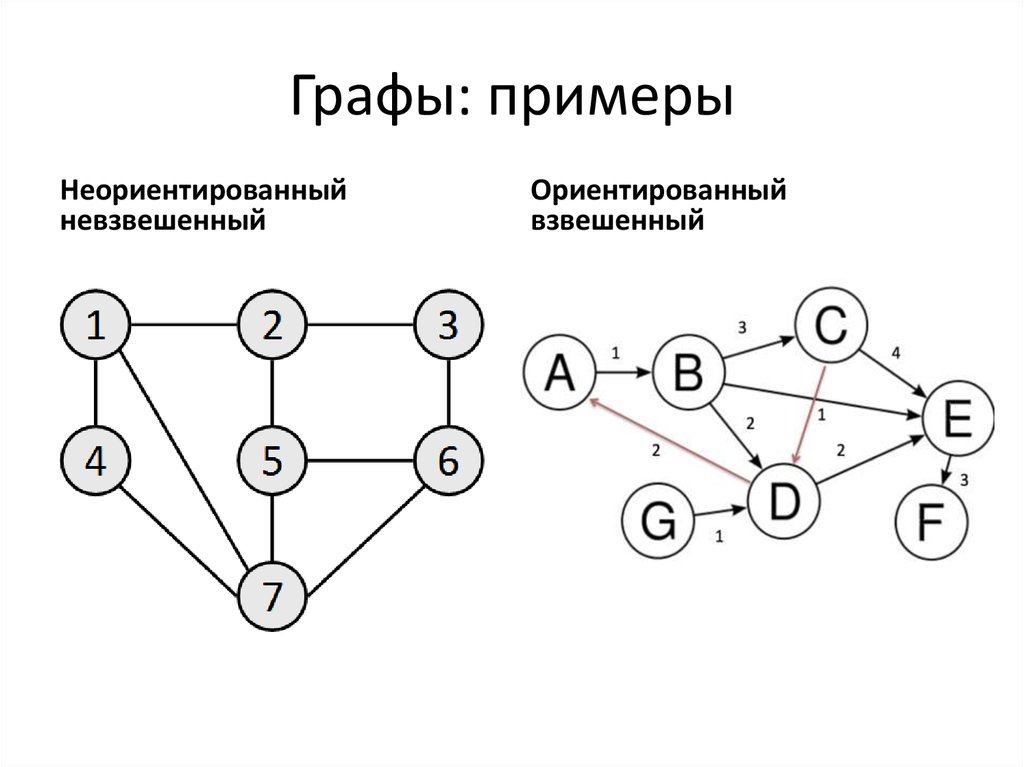
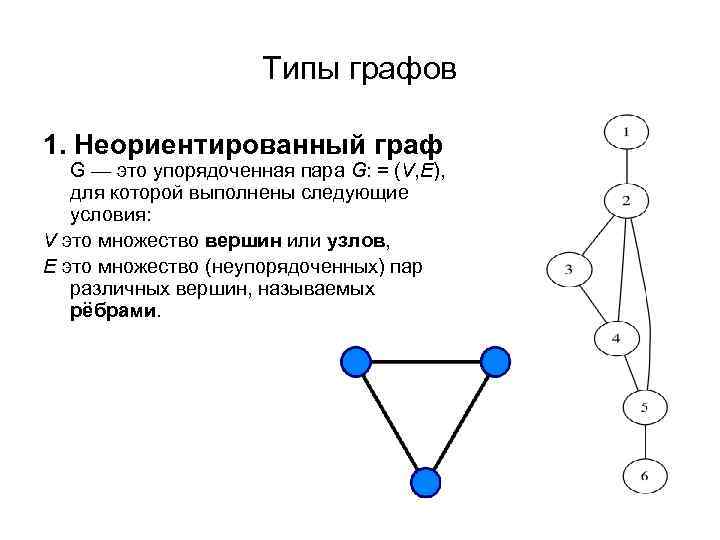
Неориентированный граф
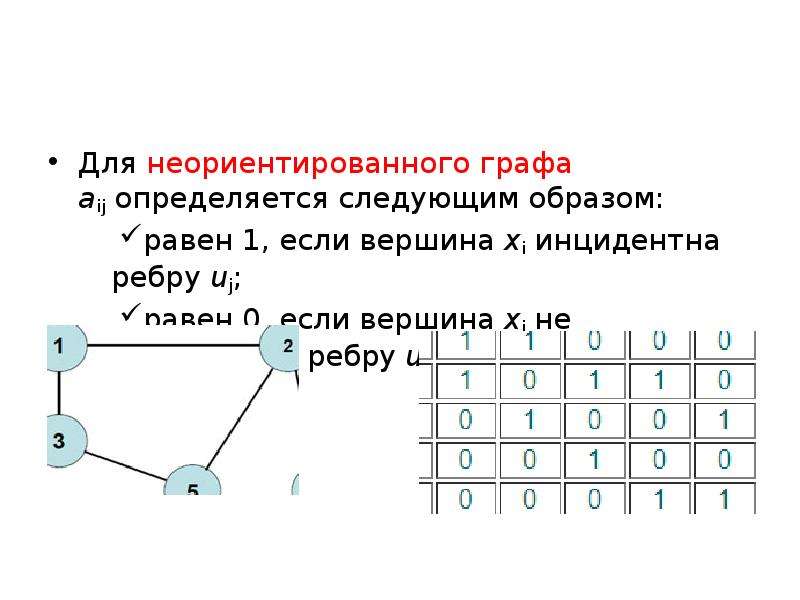
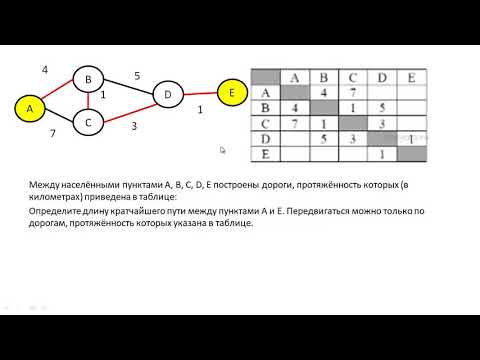
Важным аспектом при работе с планарными графами является использование алгоритмов поиска в глубину (DFS) или поиска в ширину (BFS) для эффективного обхода графа.

5-часовой веб по ГРАФАМ

Используйте методы разбиения графа на компоненты связности, чтобы упростить задачу анализа и поиска оптимальных решений в сложных планарных структурах.

Разбор 1 Задания. Графы - ЕГЭ информатика - Артем Пальчиков. Информатика. Онлайн школа EXAMhack

Для нахождения планарных графов, которые не допускают нахождение определённых подграфов (например, K5 или K3,3), применяйте теорему Куртеса, которая помогает в решении задач 3-раскрашиваемости.

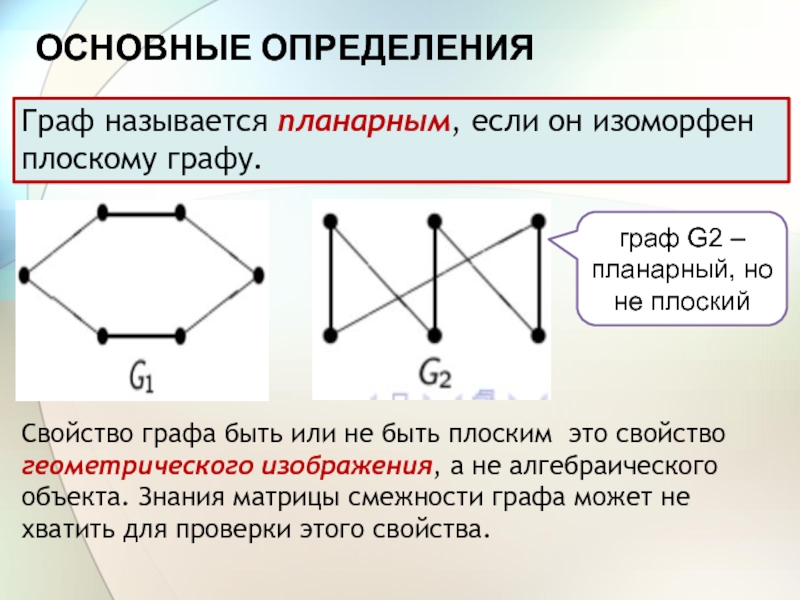
Планарные графы


Для оптимизации работы с графами применяйте различные структуры данных, такие как матрицы смежности или списки смежности, в зависимости от размера и плотности графа.

Планарные графы
Не забывайте о важности использования корректных алгоритмов для планарных графов, таких как алгоритм Прима или Краскала для нахождения минимального остова, что особенно важно при моделировании реальных сетей.
При анализе планарных графов важно помнить о том, что не все графы можно представить как планарные, поэтому перед началом работы стоит проверить граф на планарность с помощью теоремы Куранта.

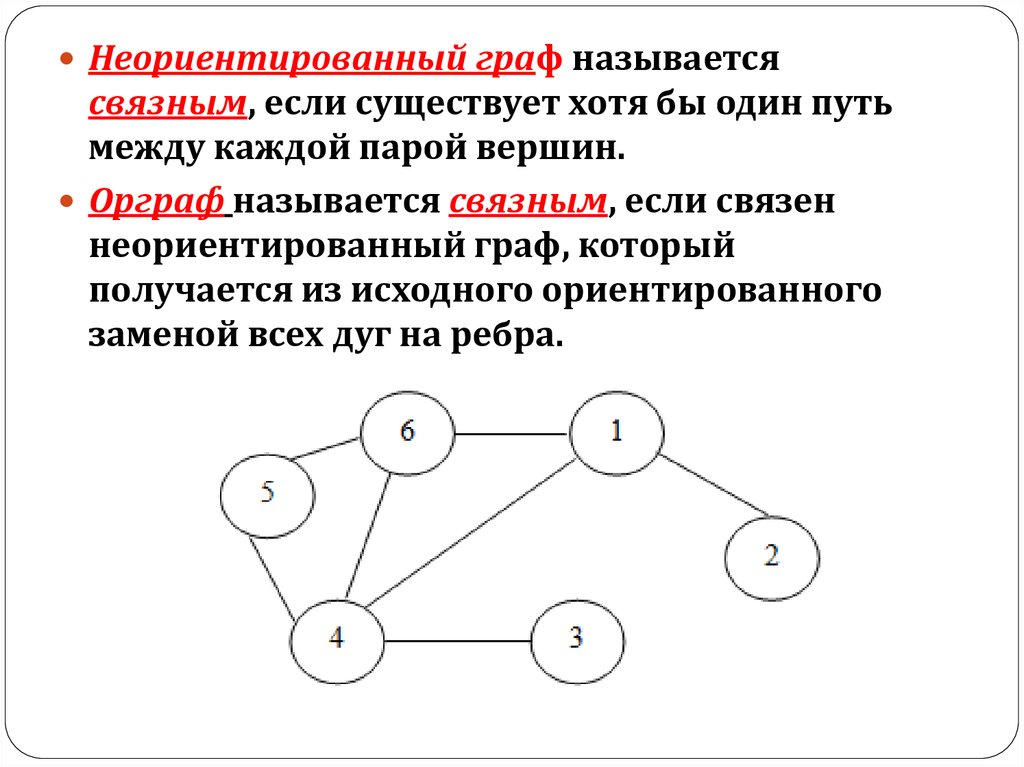
Планарные графы
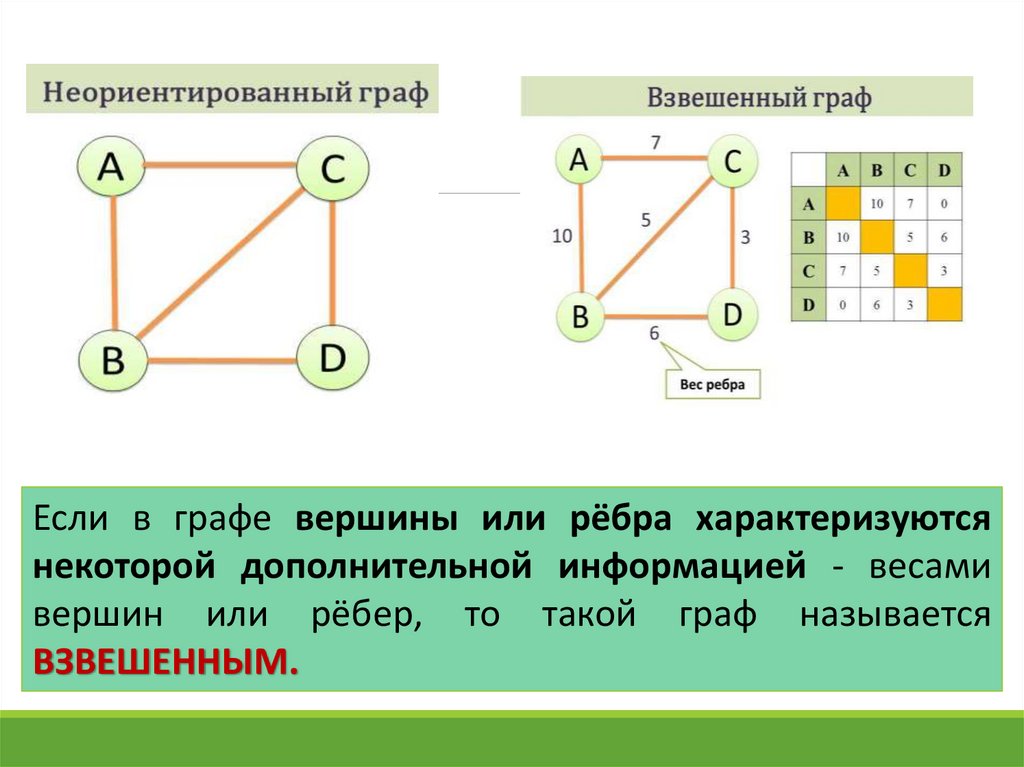

Не стоит забывать о вычислительной сложности различных операций с графами. Например, проверка на планарность может быть дорогой операцией, поэтому важно выбирать оптимальные подходы для решения задачи.

Плоские графы. Формула Эйлера
4 Непланарность графа Петерсена