Определение расстояния между точками с помощью координат для нахождения стороны треугольника
В этой статье представлены советы и методы, как найти длину стороны треугольника по координатам его вершин. Этот процесс включает в себя использование формулы расстояния между двумя точками на плоскости, что является основой для расчета длины стороны в треугольнике. Мы рассмотрим подробные примеры и полезные советы для удобства и точности вычислений.


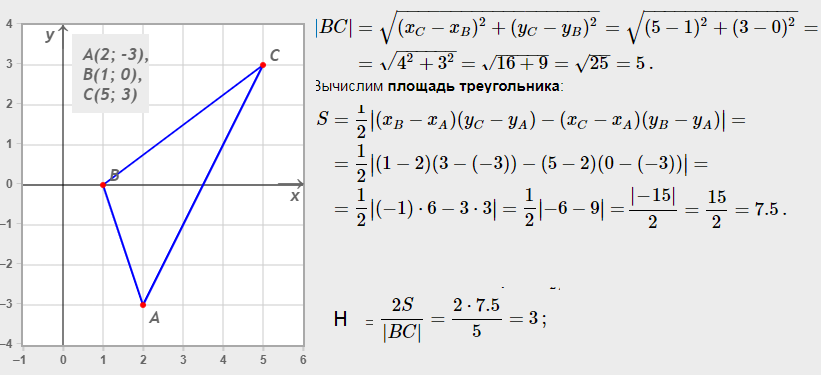
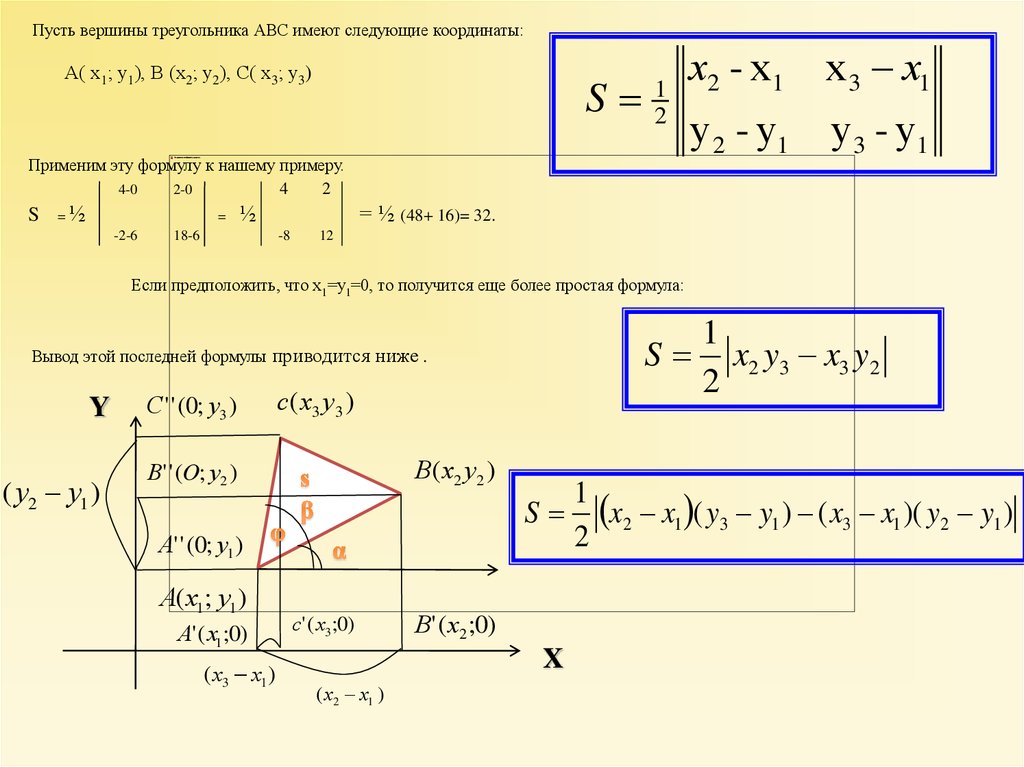
Для вычисления длины стороны треугольника по координатам, используйте формулу расстояния между двумя точками: √((x2 - x1)² + (y2 - y1)²).

Метод координат. Как найти медиану треугольника, если известны координаты его вершин?


Помните, что для нахождения всех сторон треугольника нужно вычислить расстояния между каждой парой вершин.

Нахождение длины отрезка по координатам

Чтобы избежать ошибок, внимательно определяйте координаты всех трех вершин, особенно если они заданы в разных системах отсчета.

Классный способ для разметки любого угла без транспортира.

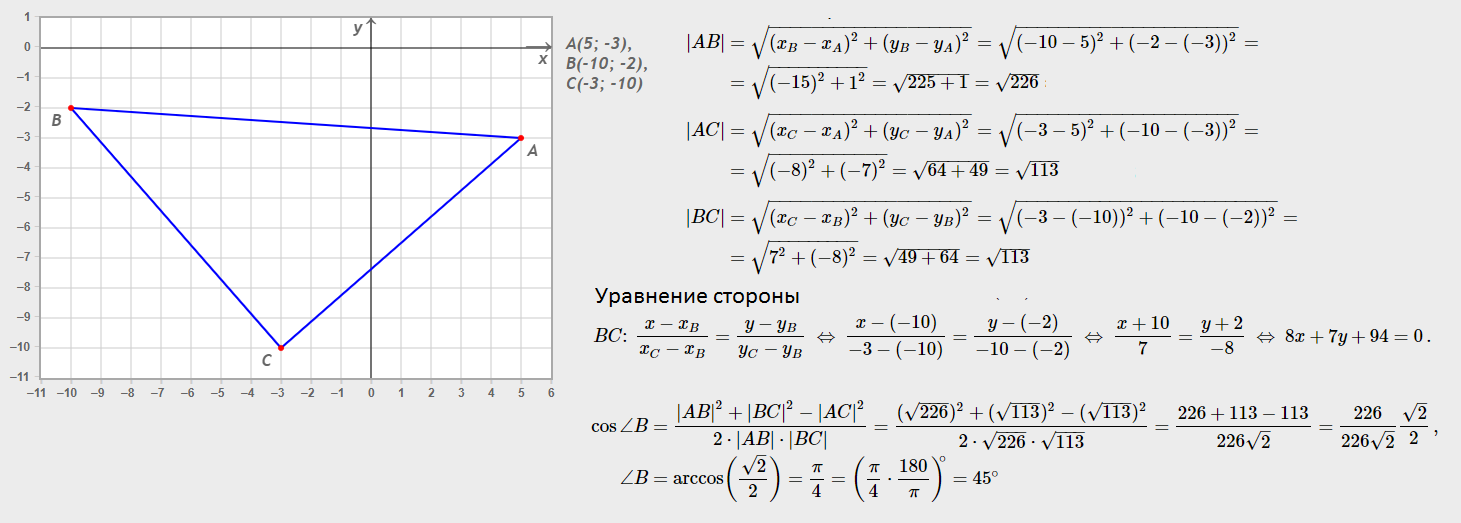
Для лучшего понимания используйте графический метод: нанесите вершины треугольника на координатную плоскость.

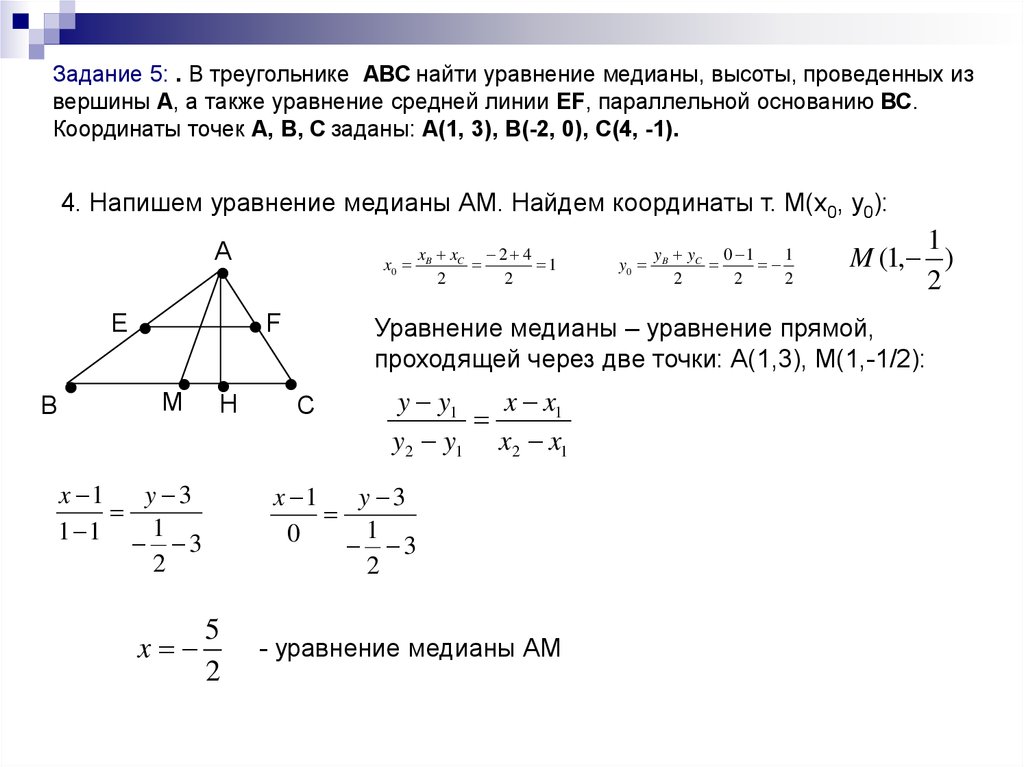
Уравнения стороны треугольника и медианы
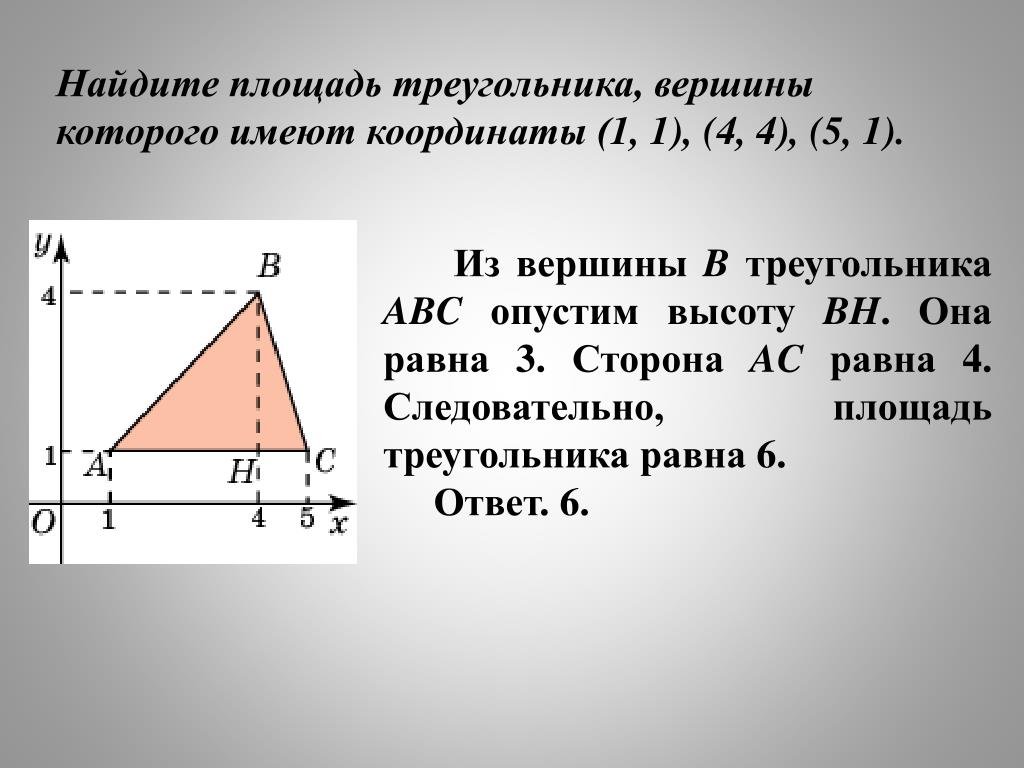
Если треугольник имеет прямой угол, используйте теорему Пифагора для упрощения вычислений длины стороны.

Азимут магнитный. Дирекционный угол. Как их определить на карте. Гринвичский меридиан.

При работе с декартовыми координатами убедитесь, что все значения координат заданы правильно: по оси X и Y.
Для вычислений используйте калькулятор или математическое ПО, чтобы минимизировать возможные ошибки при извлечении корня.

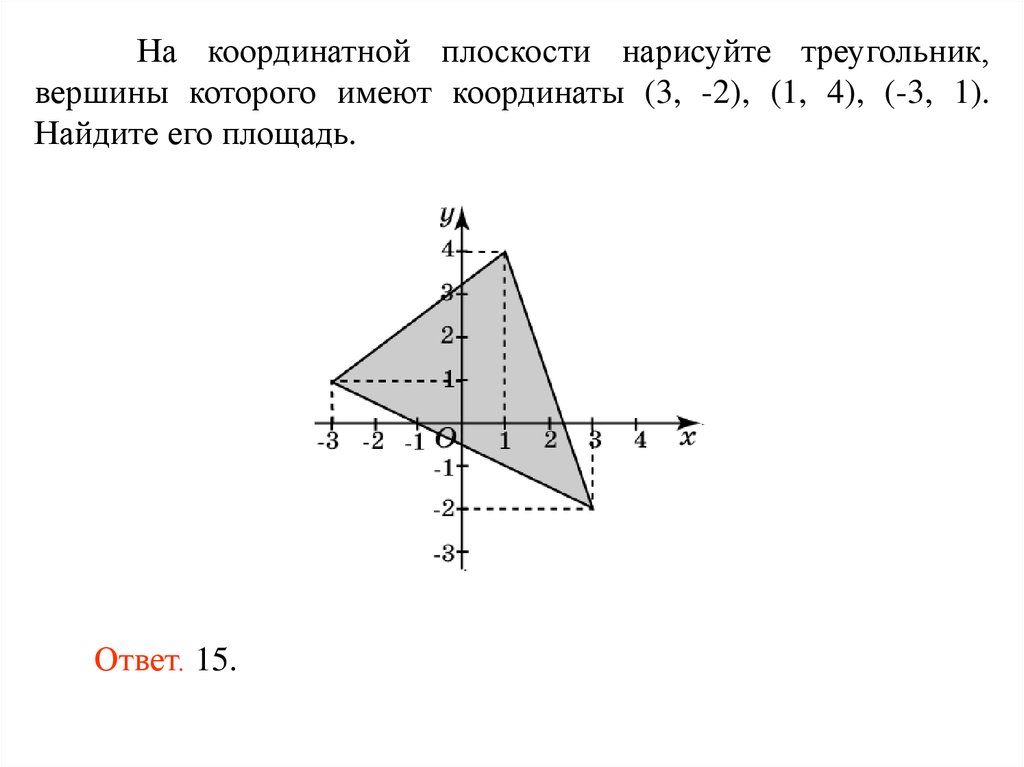
Важно помнить, что порядок координат в формуле не влияет на результат, так как квадрат разности всегда положительный.
Для точных расчетов можно использовать более сложные методы, такие как матричные вычисления, если треугольник задан в трехмерной системе координат.
как найти диагональ.
При работе с большими наборами данных лучше использовать программирование для автоматизации вычислений длин сторон треугольников.
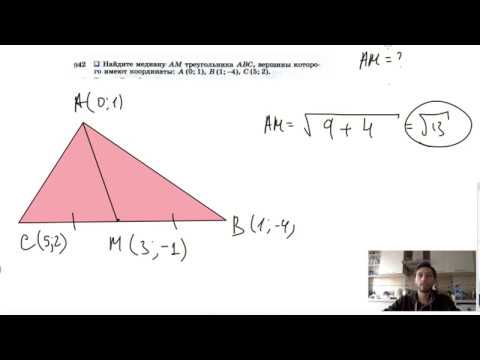
№942. Найдите медиану AM треугольника ABC, вершины которого имеют координаты: А(0; 1), В(1; -4)