Основные методы поиска минимального остовного дерева в графах
Минимальное остовное дерево графа является важной задачей в теории графов, решаемой с помощью различных алгоритмов, таких как алгоритм Прима и Краскала. На этой странице собраны полезные советы и методы для поиска оптимальных решений, которые помогут вам глубже понять и эффективно применять эти алгоритмы на практике.

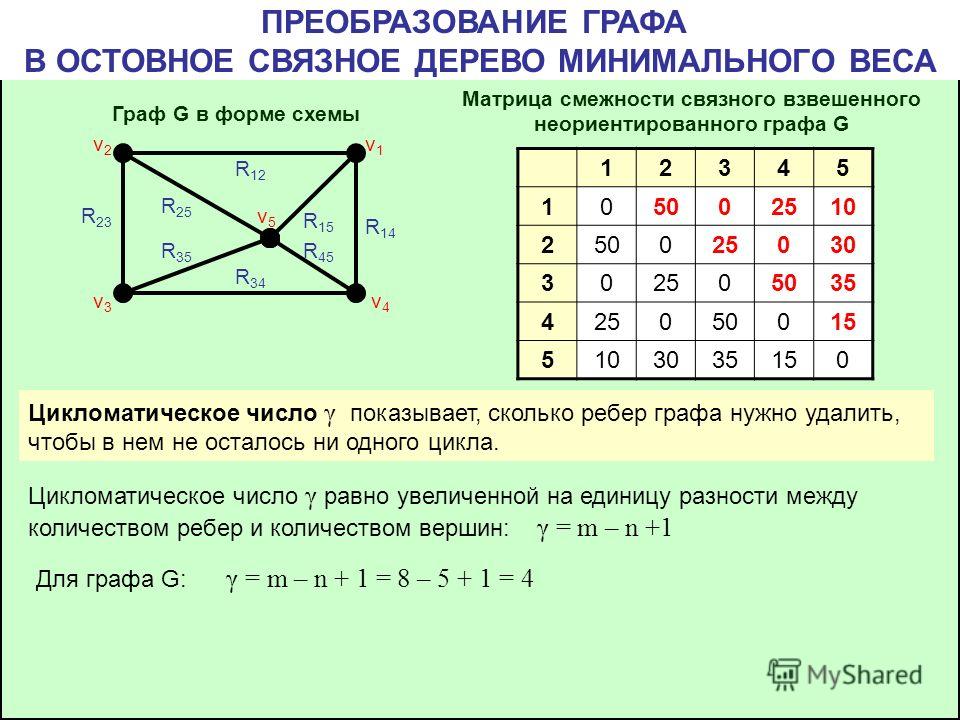
Используйте алгоритм Краскала для графов с разреженной связностью.

Лекция 11. Минимальное остовное дерево

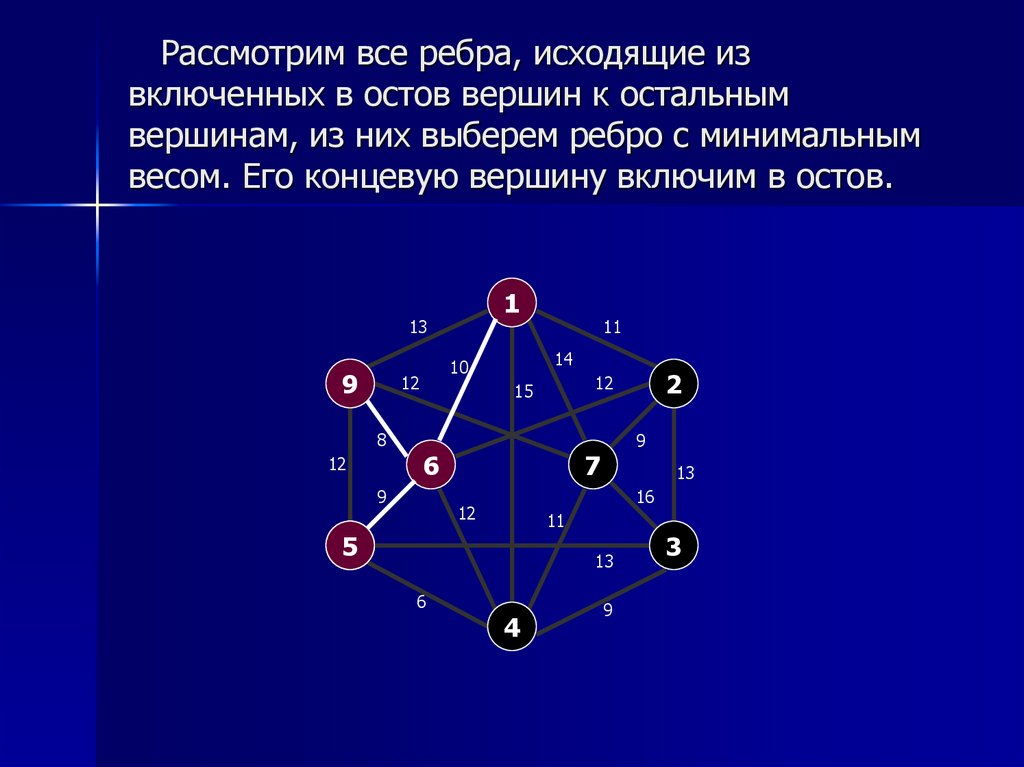
Алгоритм Прима более эффективен для плотных графов с большим количеством рёбер.
15. Поиск кратчайшего пути и построение минимального остовного дерева

Проверьте граф на наличие циклов перед применением алгоритмов поиска остовного дерева.
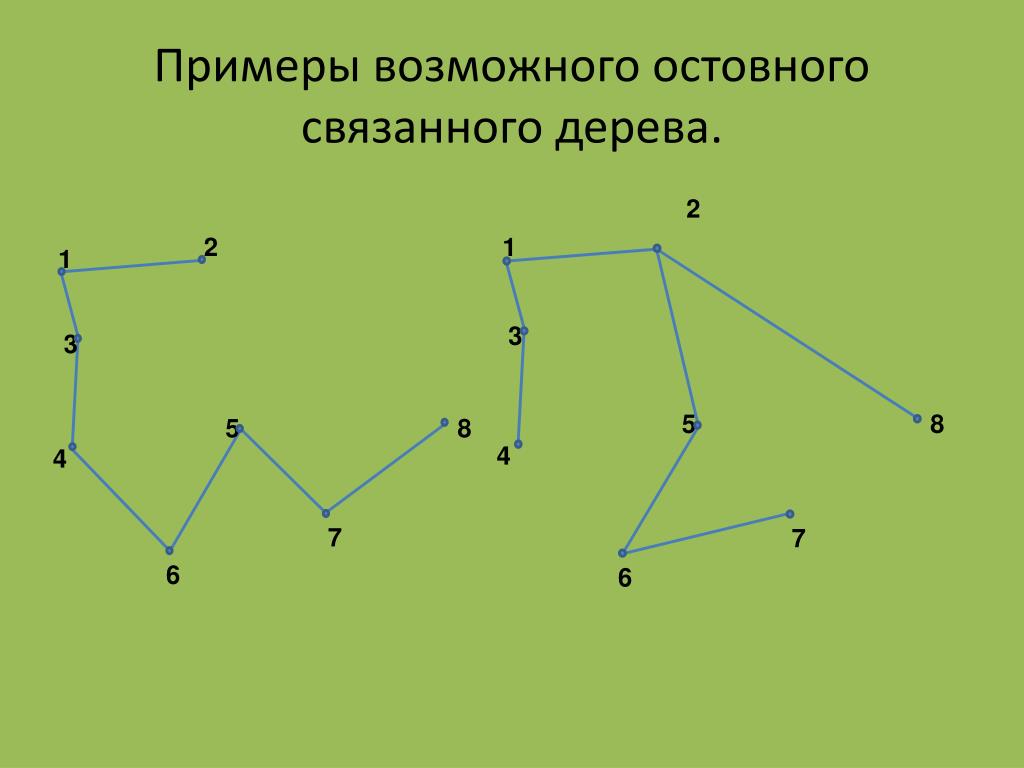
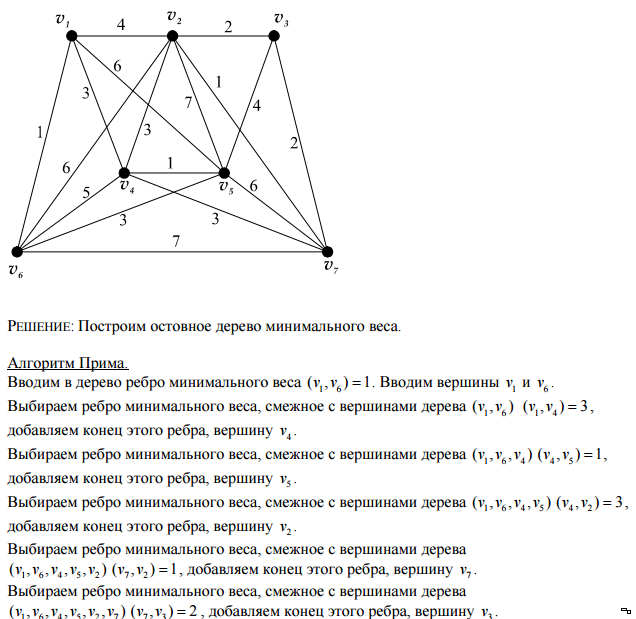
Построение минимального остовного дерева графа. Метод Прима.
Для реализации алгоритма Краскала используйте структуру данных «объединение-по-рангу».
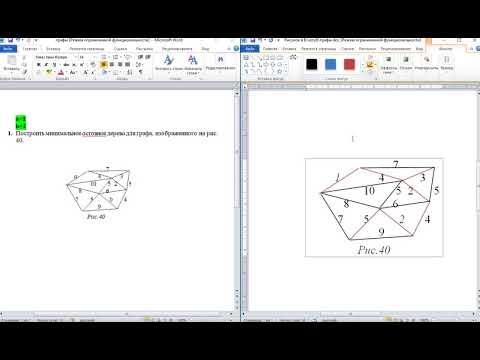
Минимальное остовное дерево

Для быстрого поиска минимального ребра в алгоритме Прима применяйте кучу Фибоначчи.

Алгоритм Краскала для поиска минимального остовного дерева во взвешенном графе

В случае нескольких равных остовных деревьев выбирайте тот, который минимизирует сумму весов рёбер.
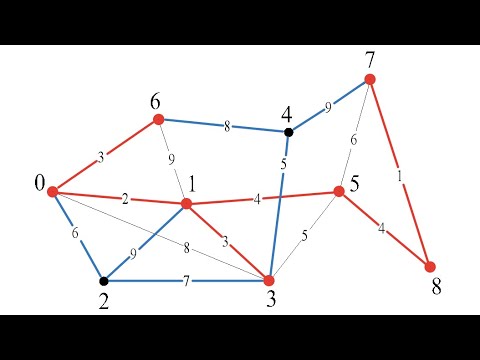
Минимальное остовное дерево. Алгоритм Прима

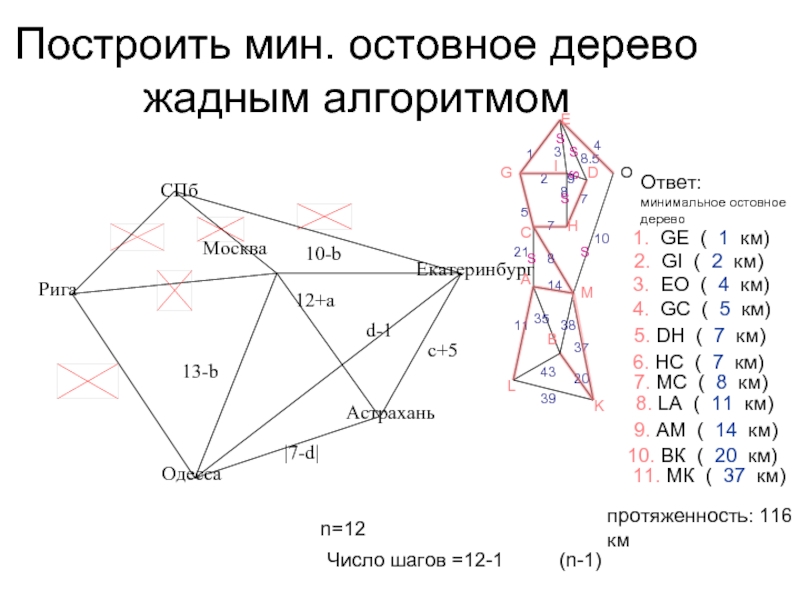
Использование жадных алгоритмов помогает быстро находить минимальные остовные деревья.
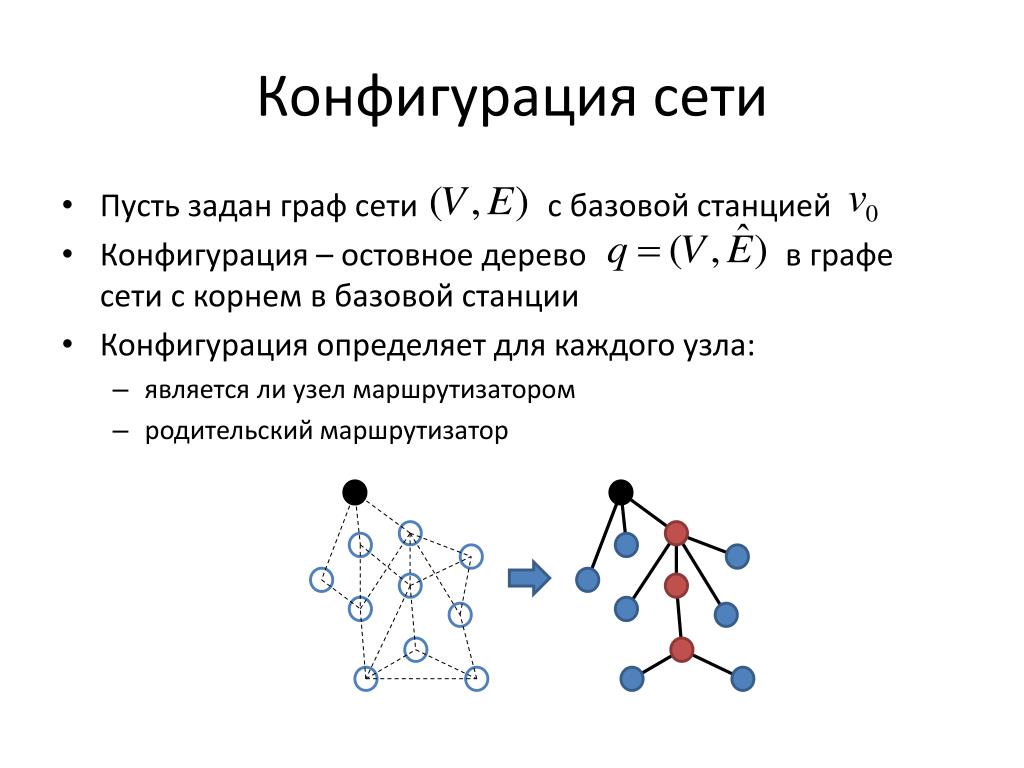
Рассматривайте возможность использования динамического программирования для сложных вариантов задачи.
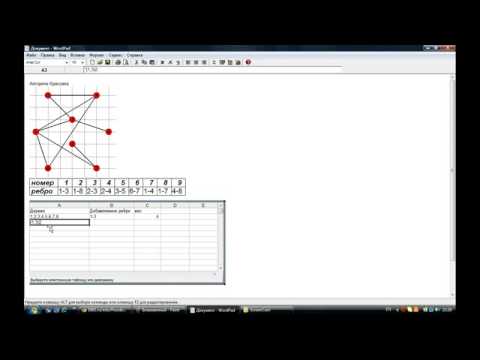
Построение минимального остовного дерева графа. Метод Краскала.
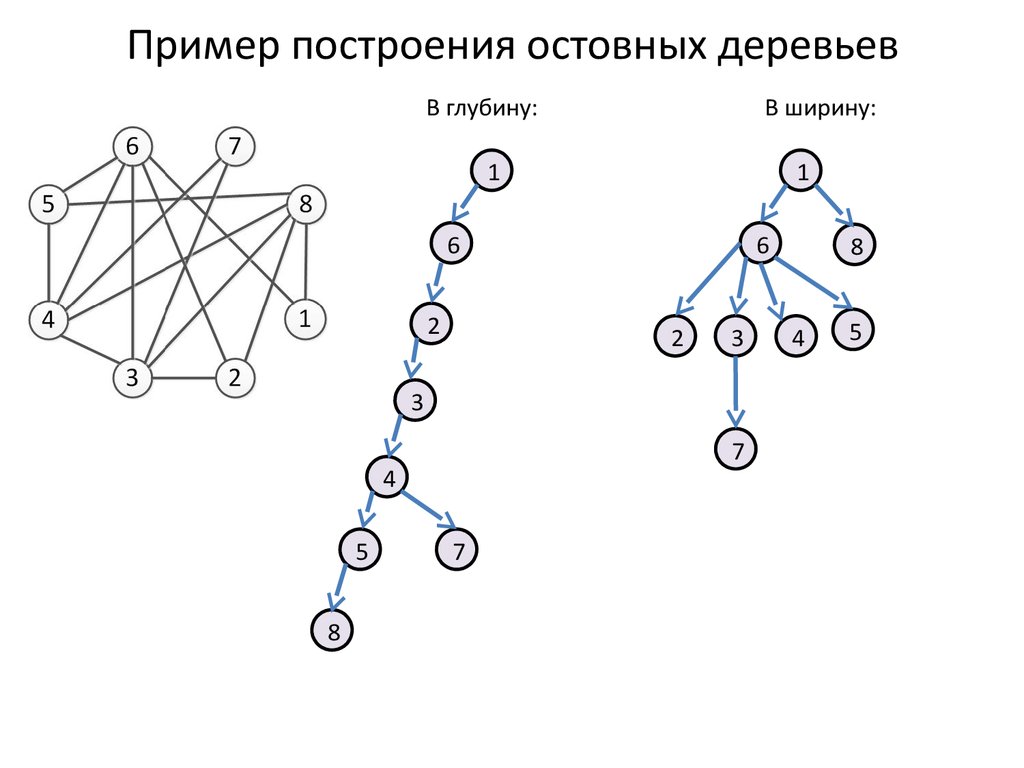
Применение эвристических методов может ускорить решение задачи в реальных приложениях.

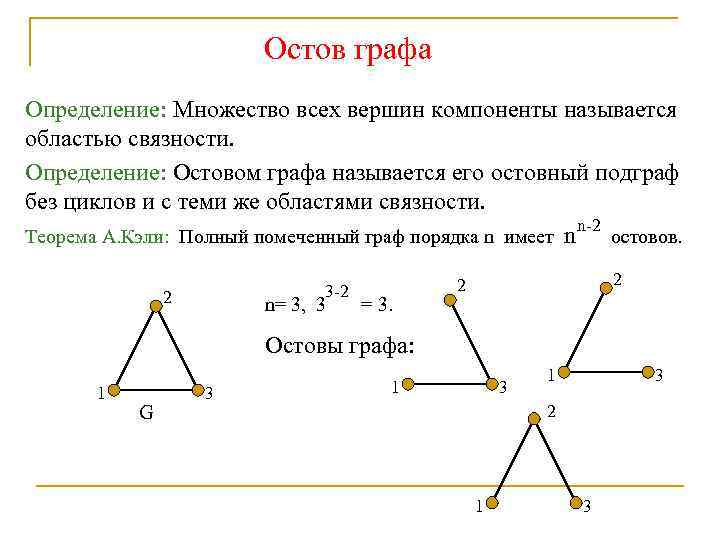
Графы. Деревья. Остов графа
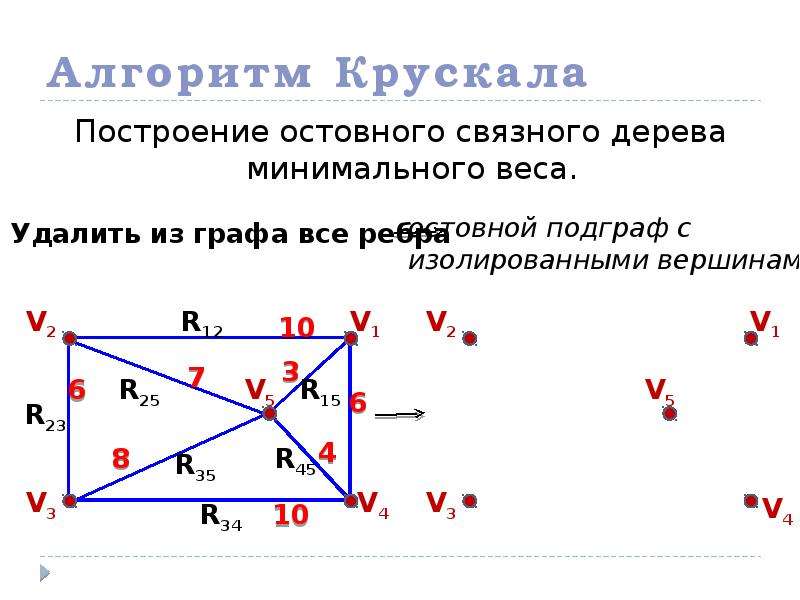
При решении задачи на больших графах используйте методы параллельной обработки для улучшения производительности.
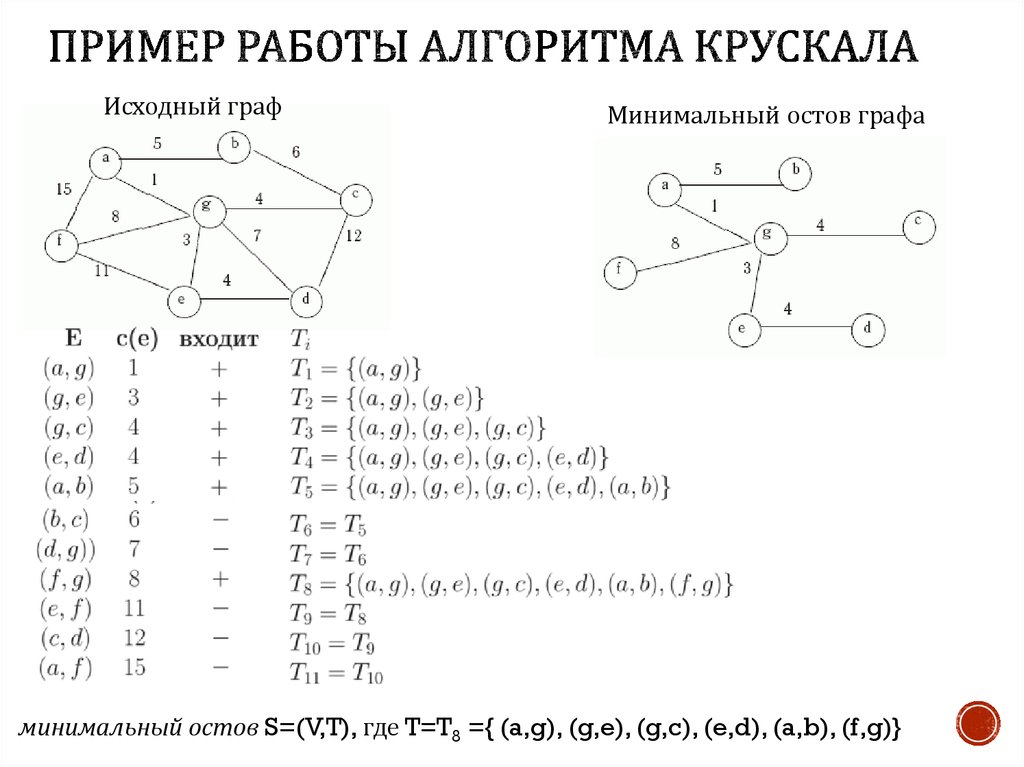

Минимальное остовное дерево графа