Множества в высшей математике: понимание и практическое применение
Множества являются основой многих концепций высшей математики, играя ключевую роль в теории чисел, анализе и других областях. Изучение их структуры и свойств позволяет глубже понять математические системы и их взаимосвязи.

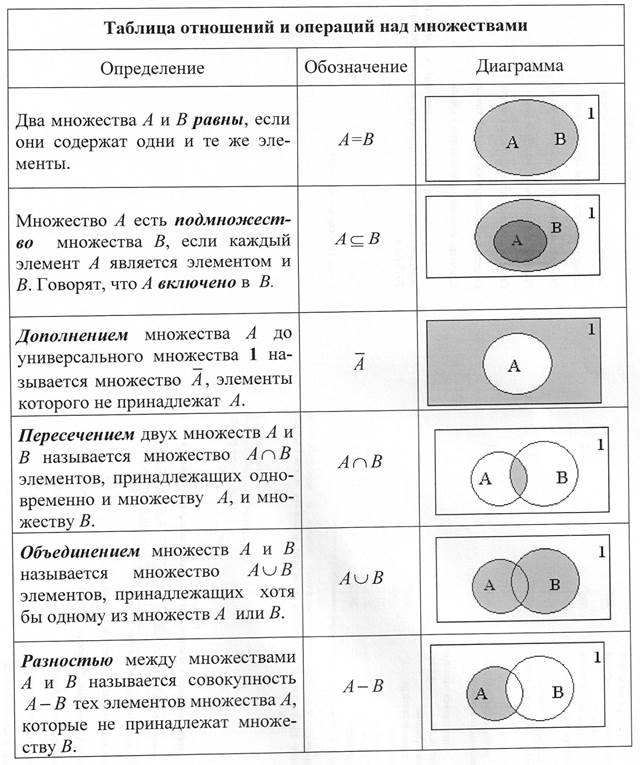
Изучение множества начинается с простых понятий, таких как элементы, объединение и пересечение.
Множество. Элементы множества. 5 класс.


Освойте операции с множествами: дополнение, разность и симметрическая разность, чтобы улучшить навыки работы с ними.

Введение в математический анализ 1. Множества и функции

Внимательно подходите к понятиям подмножества и супермножества, так как они являются основой для многих теорем.

Множества — Принципы математического мышления — уровень 5 из 5
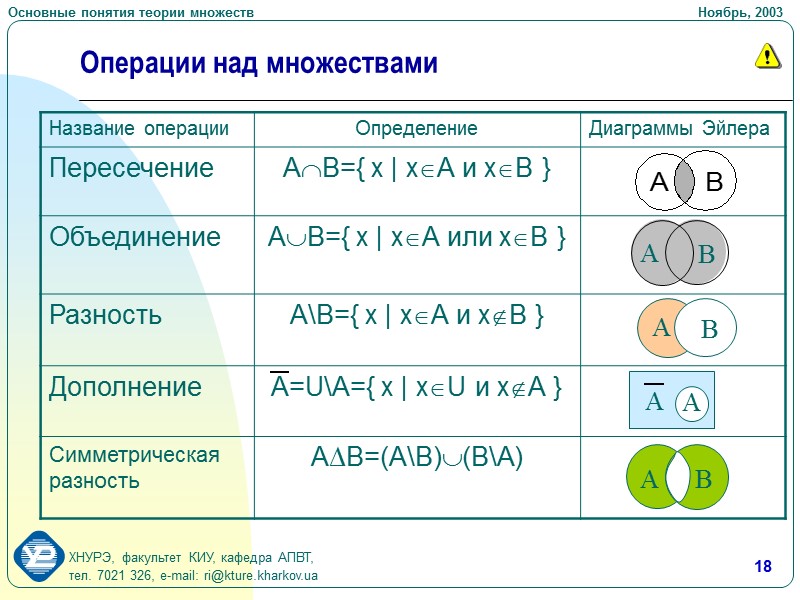
Часто полезно визуализировать множества с помощью диаграмм Венна для лучшего понимания их взаимодействий.

✓ Введение в математический анализ. Множество действительных чисел - матан #001 - Борис Трушин
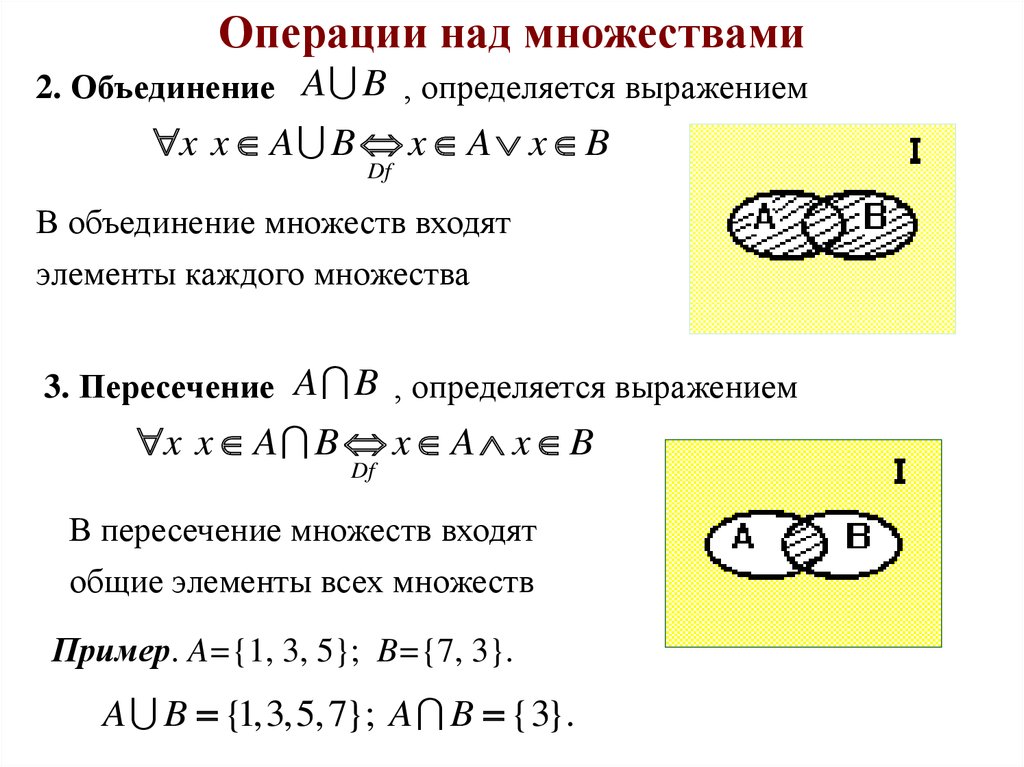
Не забывайте о кардинальности множества, особенно при работе с бесконечными множествами.
КАК РАЗОБРАТЬСЯ В ВЫСШЕЙ МАТЕМАТИКЕ


Изучите аксиомы теории множеств, такие как аксиома выбора и аксиома регулярности, чтобы глубже понять структуру множеств.

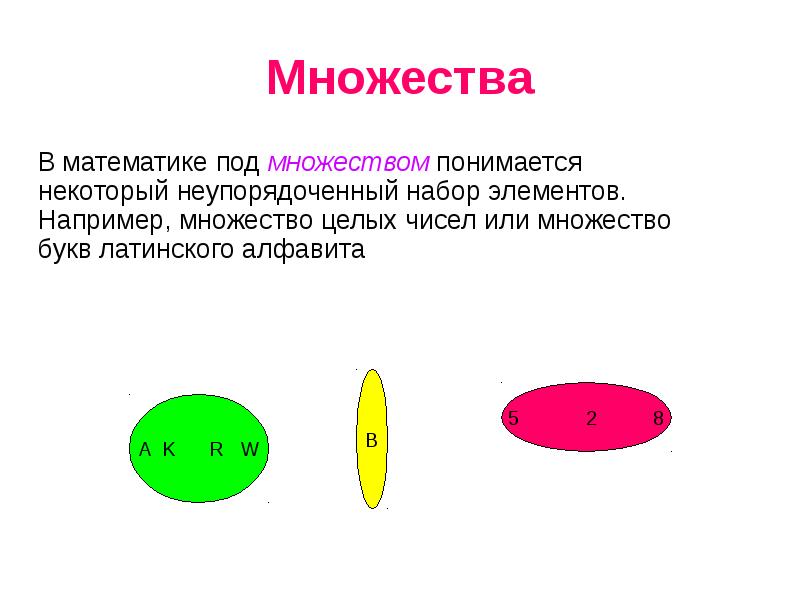
Понимание различий между конечными и бесконечными множествами крайне важно для решения более сложных задач.

SSC Higher Math 2025( উচ্চতর গণিত ) -- Chapter 1(1.1) -- সেট ও ফাংশন -- Set and Function // Part 1
Практикуйтесь на решении задач, используя свойства различных типов множеств (например, открытые, замкнутые множества).

9 класс, 2 урок, Множества и операции над ними

Изучите методы доказательства, такие как доказательство от противного, которые часто используются при работе с множествами.

Множества и операции над ними


Обратите внимание на важность теории множеств в других областях математики, таких как топология и теория вероятностей.
