Разнообразие методов нахождения решений для уравнений параболы
Параболы играют важную роль в различных областях математики и физики. На этой странице собраны разнообразные способы решения задач, связанных с параболами, а также полезные советы, которые помогут вам понять основные методы и их применения.

Для решения уравнений параболы часто используется метод выделения полного квадрата, что позволяет преобразовать уравнение в удобную форму.
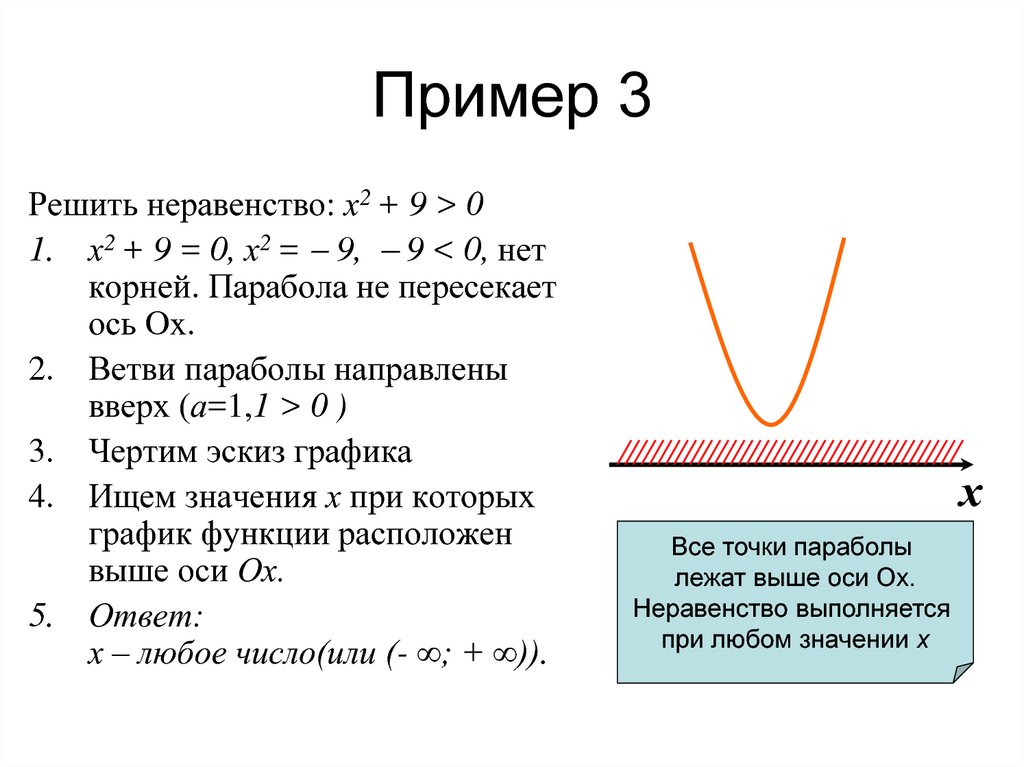
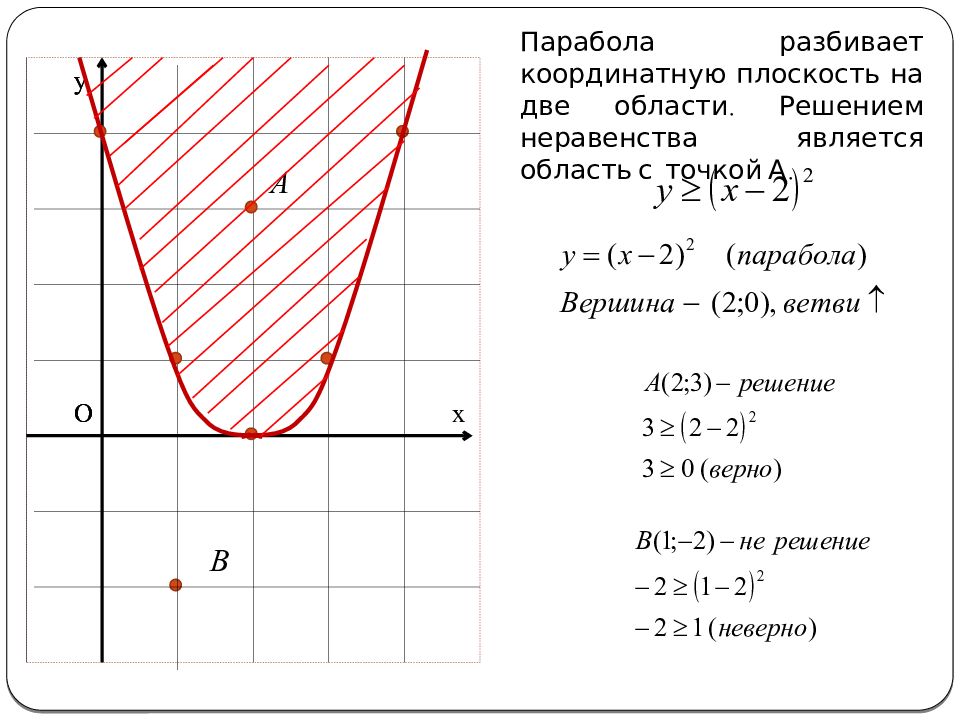
Квадратное неравенство. Бесконечное множество решений


Внимательно анализируйте координаты вершины параболы, они могут значительно упростить решение задачи, если использовать их для нахождения экстремума функции.
Математика 4 класс. Решение неравенства. Множество решений
Если у вас есть уравнение параболы в каноническом виде, сразу можно определить её фокус и директрису, что полезно для многих задач.

Как понять неравенства? Квадратные неравенства. Линейные и сложные неравенства - TutorOnline
Использование симметрии параболы может помочь в упрощении вычислений, особенно если задача имеет симметричную структуру.

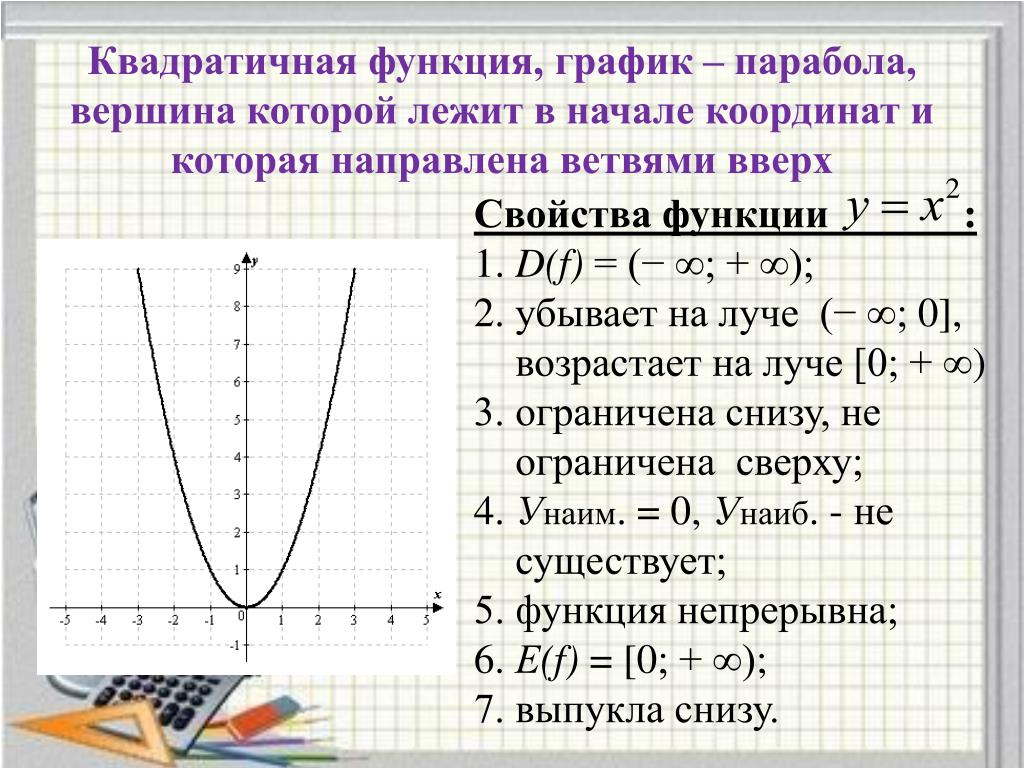
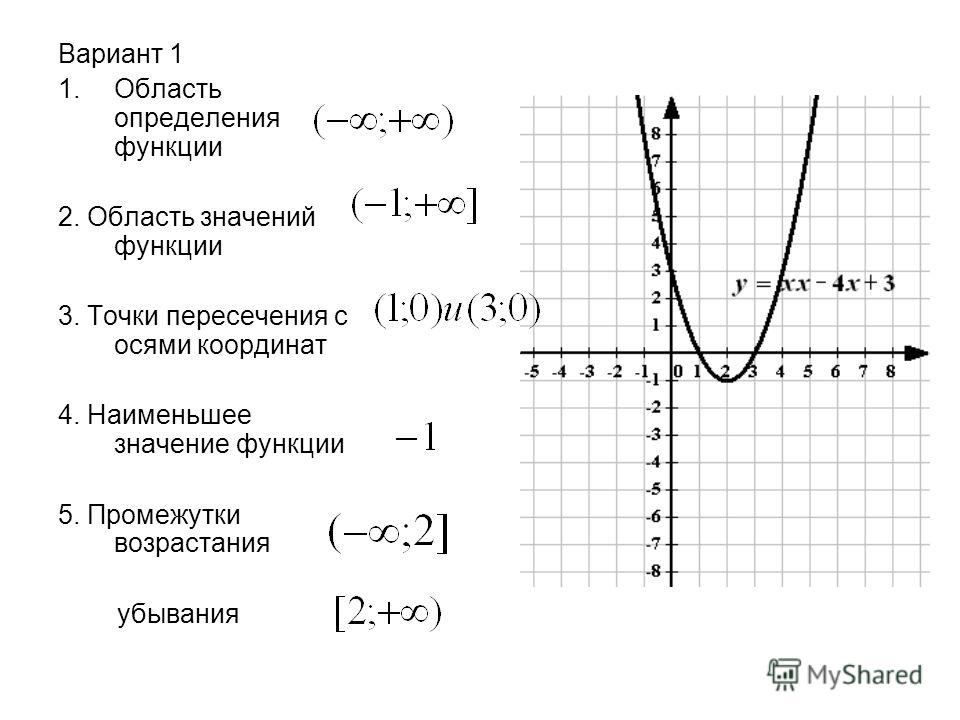
Всё о квадратичной функции. Парабола - Математика TutorOnline
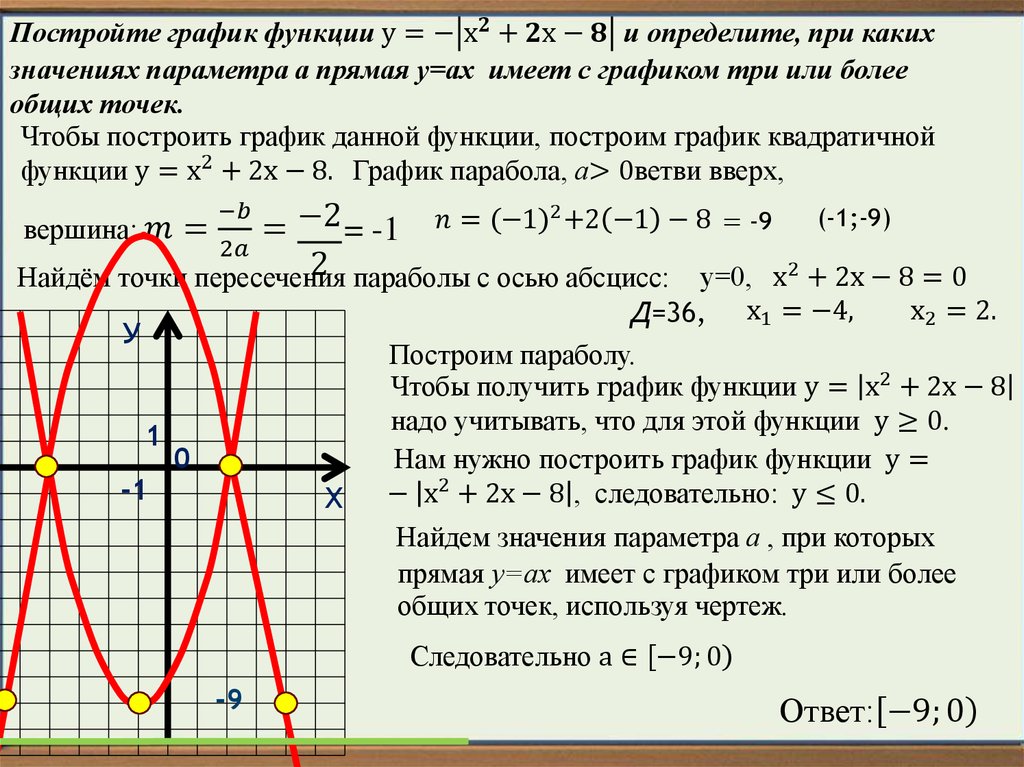
При решении задач, связанных с параболами, полезно помнить о свойствах фокуса и директрисы, которые могут помочь в геометрическом решении.

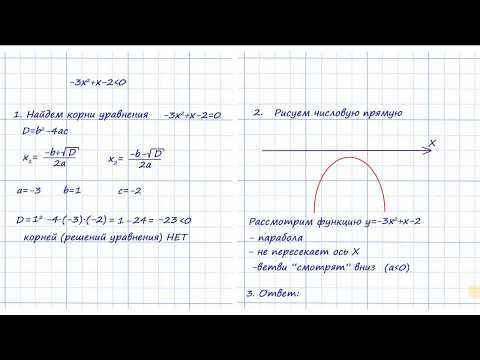
Решение квадратных неравенств - Математика
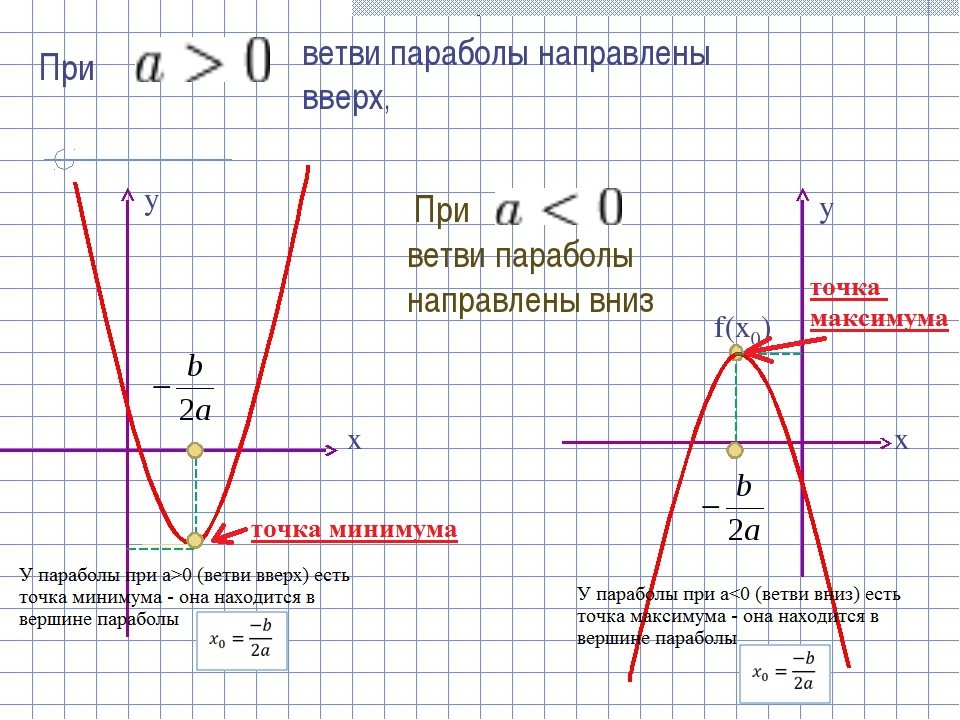
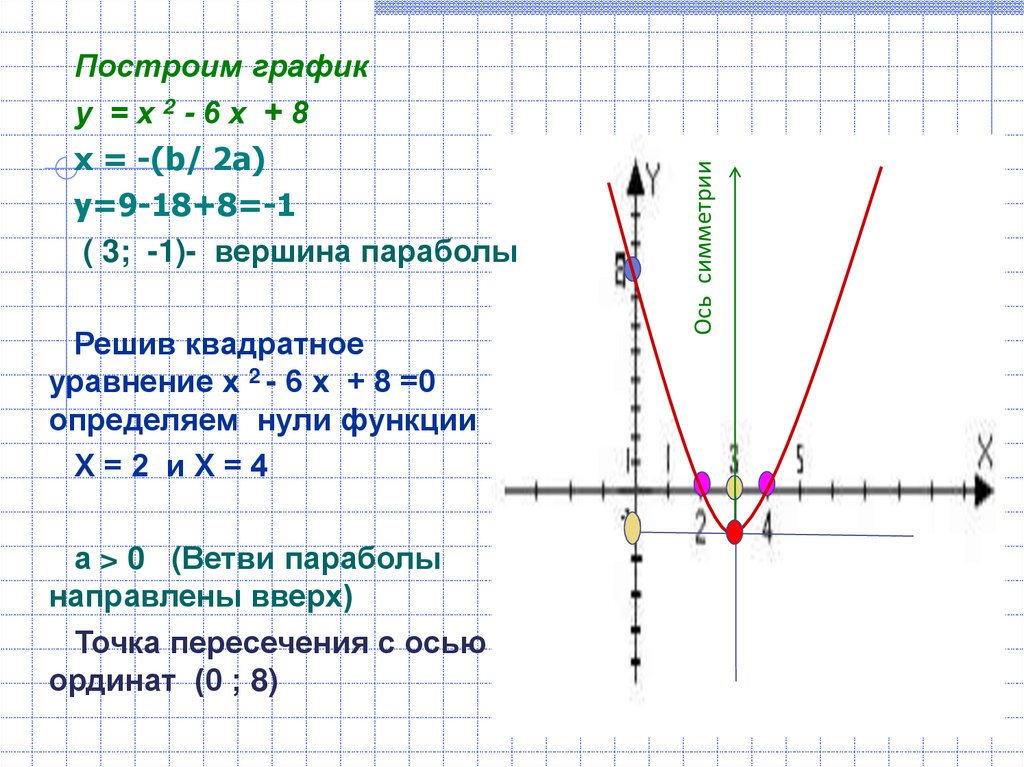
Не забывайте про метод касательных, который помогает найти точки касания параболы с прямой, а также их координаты.

ЭЛЕМЕНТАРНО, ВАТСОН! Квадратичная Функция и ее график Парабола
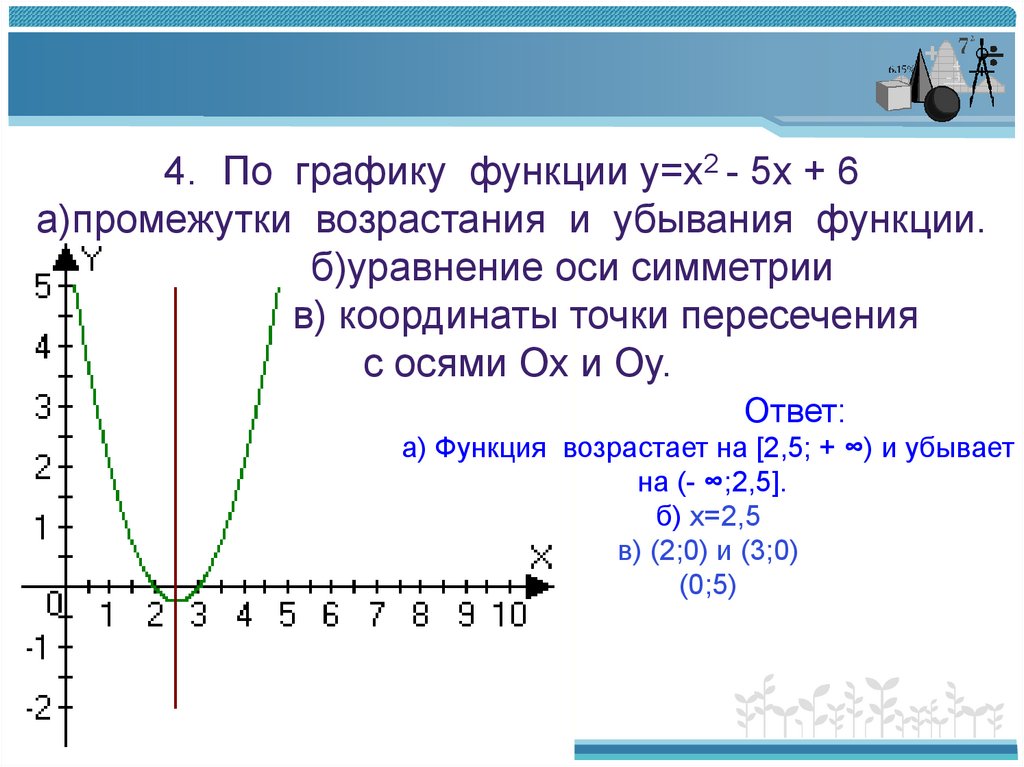
При анализе параболы важно учитывать её ориентацию (вверх, вниз, влево, вправо), так как это влияет на расположение вершин и фокуса.

1. Решение квадратных неравенств с помощью параболы.
Если парабола задана не в стандартном виде, преобразование уравнения в каноническую форму может значительно упростить решение.

Решение квадратных неравенств методом интервалов. 8 класс.
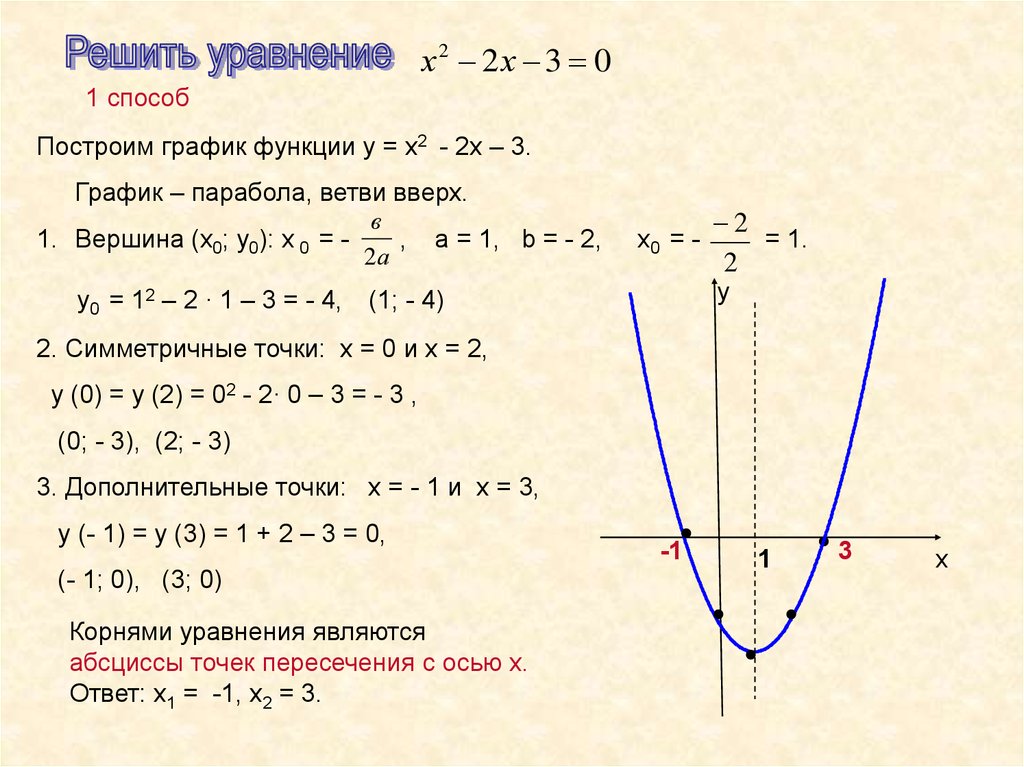
Использование производных и методов нахождения критических точек также может быть полезным для нахождения минимумов и максимумов параболической функции.
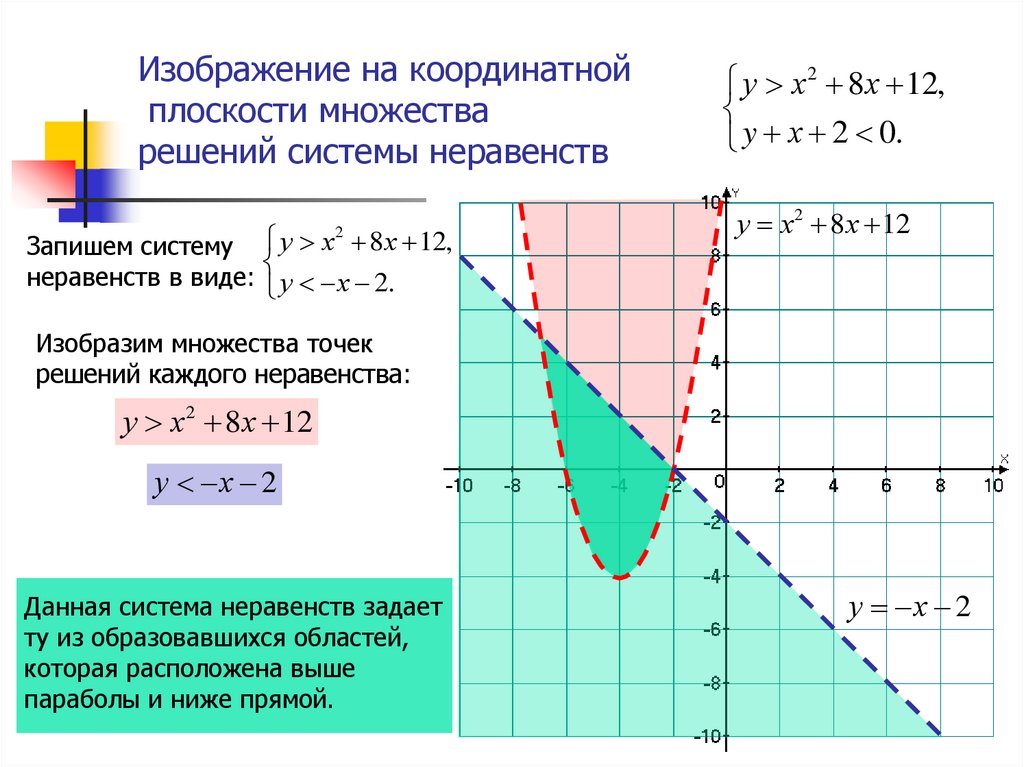

Практика с графиками парабол помогает лучше понять их форму и свойства, а также способы нахождения решений с помощью графических методов.