Как найти координаты равностороннего треугольника на координатной плоскости: пошаговое руководство
Данная страница содержит подробные инструкции и советы по нахождению координат вершин равностороннего треугольника на плоскости. Вы узнаете, как правильно вычислить координаты, используя геометрические принципы и формулы, а также какие полезные методы применимы для различных задач в математике и инженерии.

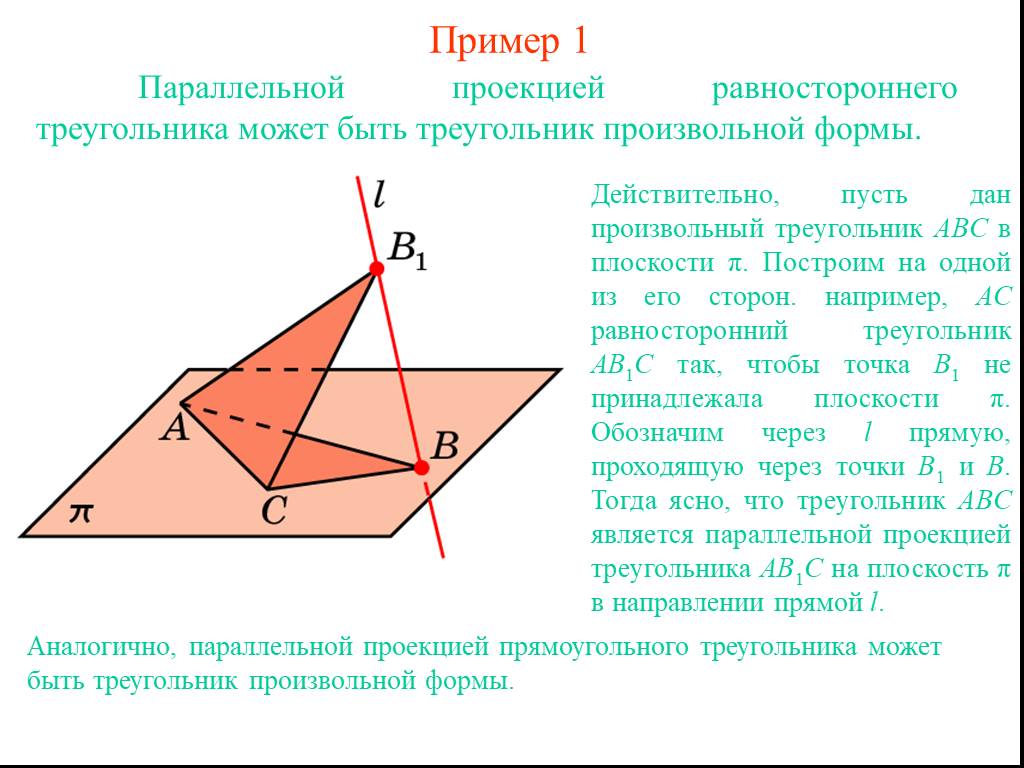
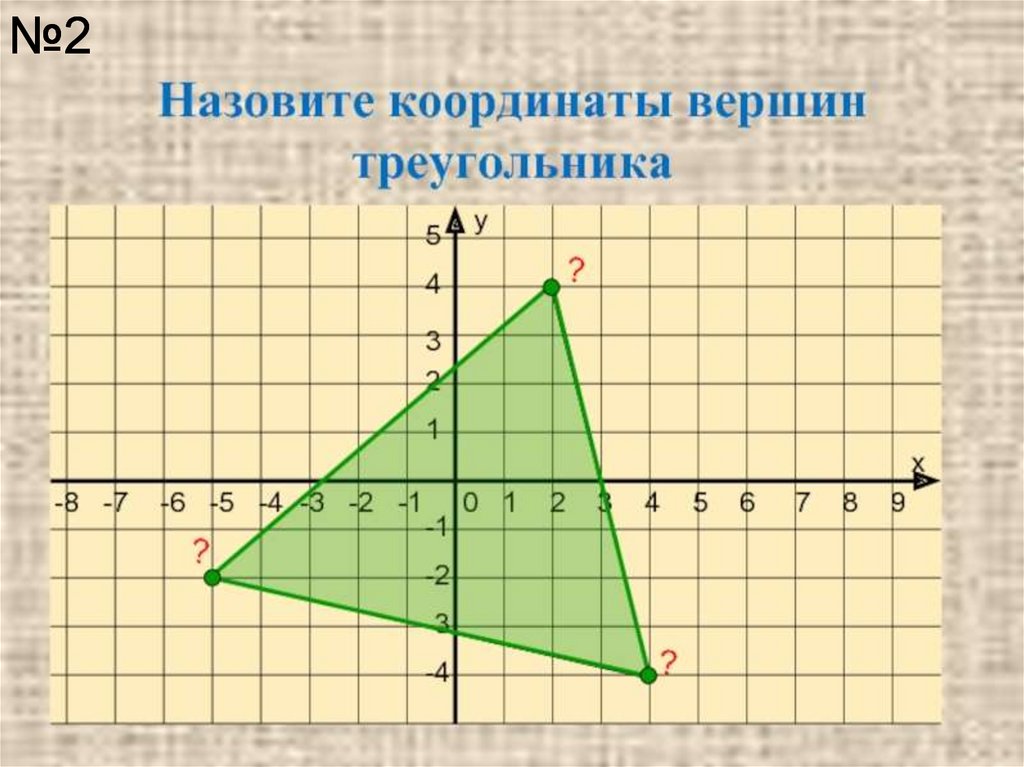
Для нахождения координат равностороннего треугольника на плоскости используйте его симметричные свойства, учитывая расположение одной вершины на оси X.

Что скрывает фрактальный треугольник? // Vital Math
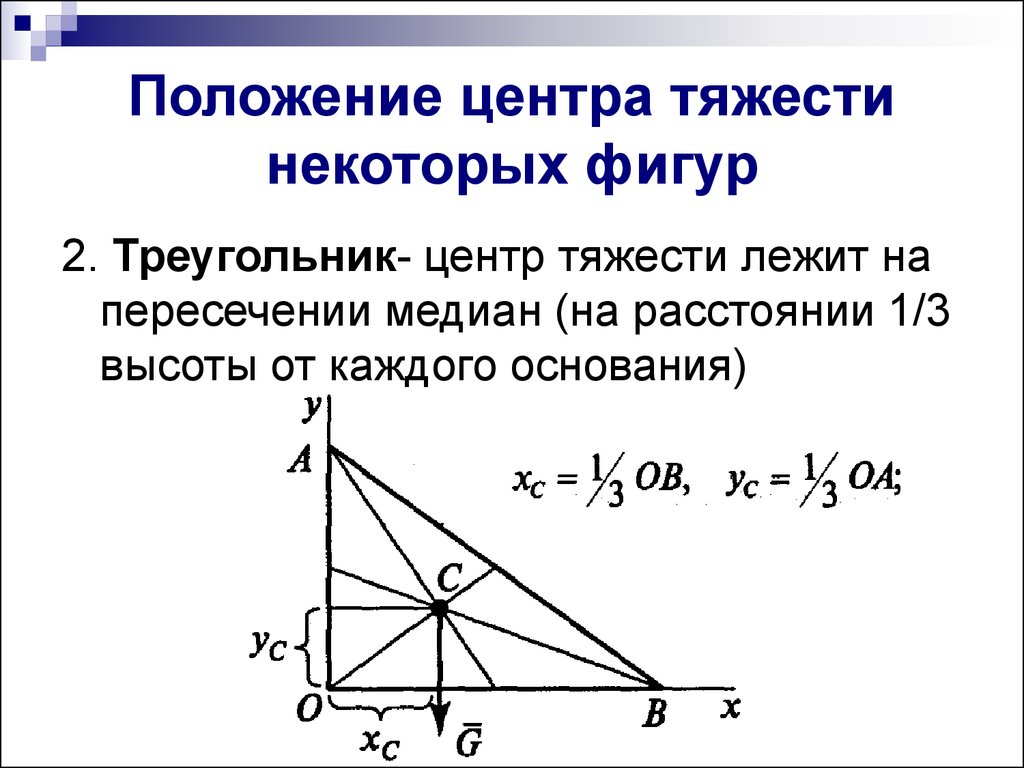
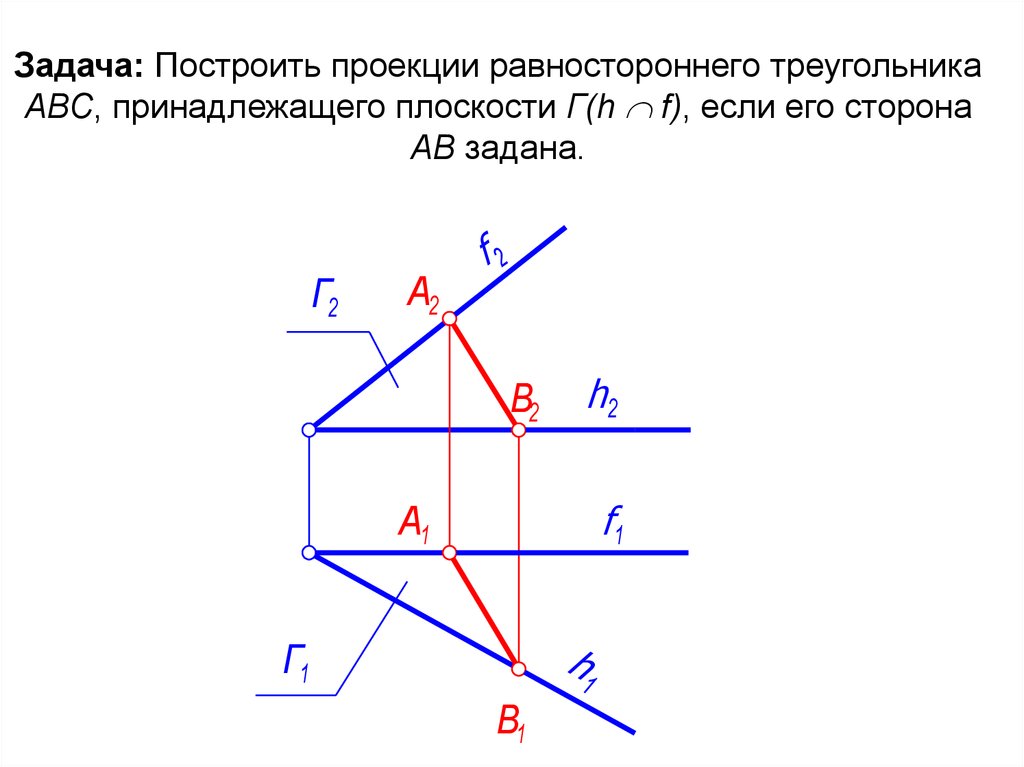
Рассматривайте равносторонний треугольник как правильный, где углы между всеми сторонами составляют 60 градусов.

Пересечение двух плоскостей. Плоскости в виде треугольника

Для точных вычислений важно выбрать правильную систему координат и правильно ориентировать треугольник относительно осей.
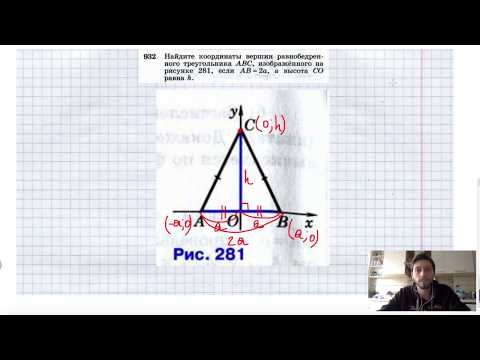
№932. Найдите координаты вершин равнобедренного треугольника ABC, изображенного на рисунке
Используйте теорему Пифагора для определения расстояний между вершинами треугольника на плоскости, чтобы проверить правильность расчетов.
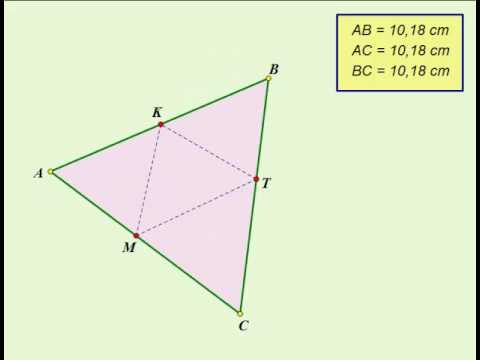
Постройте равносторонний треугольник по трём точкам на его сторонах
Для нахождения координат другой вершины, используйте формулу для расстояния между точками и угол 60 градусов между сторонами треугольника.
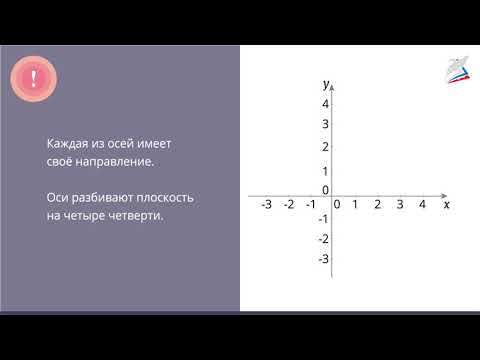
Декартова система координат на плоскости
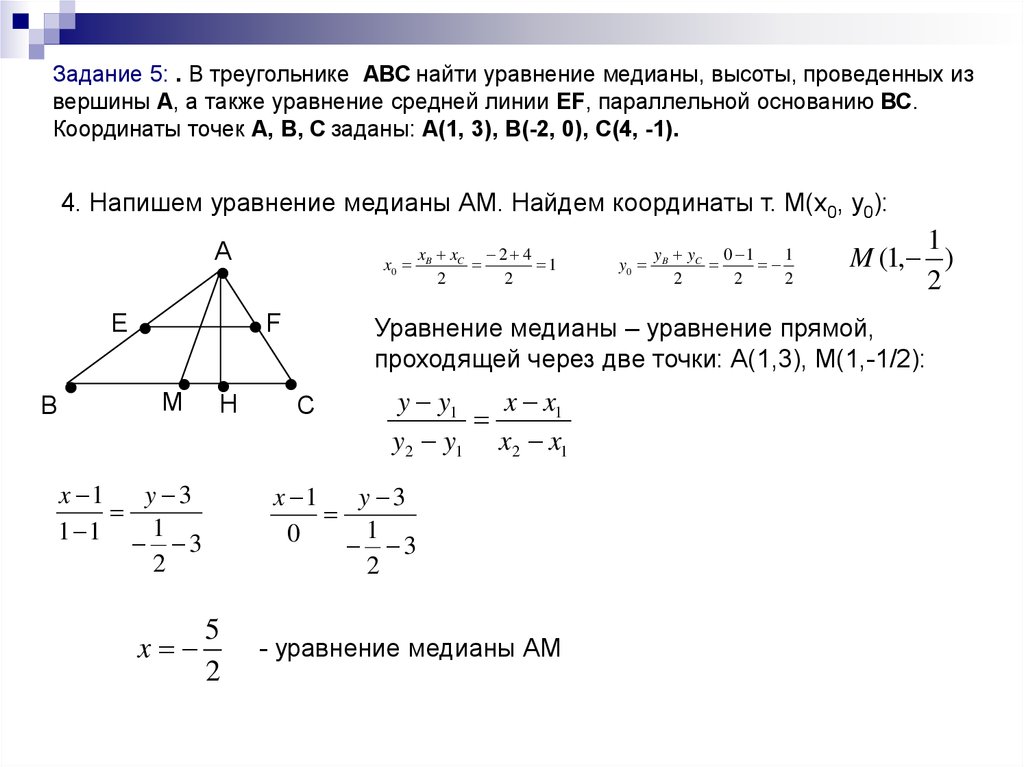
При вычислениях учитывайте, что стороны равностороннего треугольника равны, а углы между ними составляют 60 градусов.

ПОСТРОИТЬ ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЬНИКА ПО ЗАДАННЫМ УСЛОВИЯМ. НАЧЕРТАТЕЛЬНАЯ ГЕОМЕТРИЯ.
Если одна вершина треугольника задана координатами, можно использовать поворот точки на угол 60 градусов для нахождения остальных вершин.
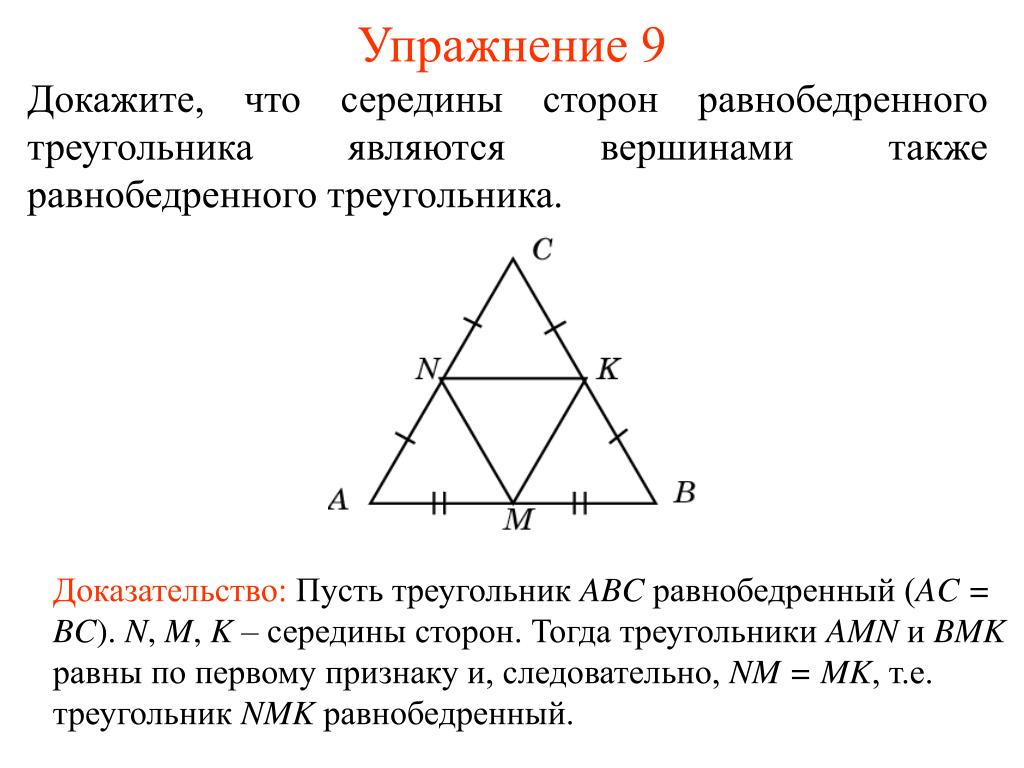

При решении задач на плоскости используйте векторы для упрощения расчетов координат равностороннего треугольника.

ПРОЕКЦИИ РАВНОСТОРОННЕГО ТРЕУГОЛЛЬНИКА НА П1/П2 и углы наклона его плоскости к плоскостям проекций
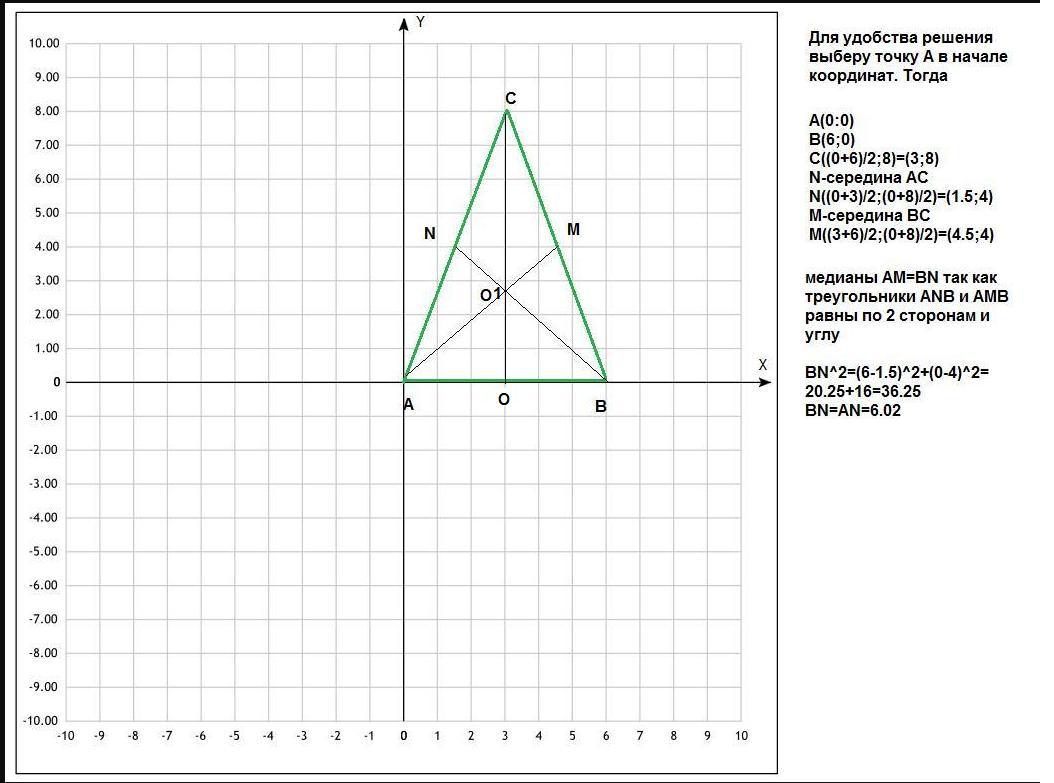
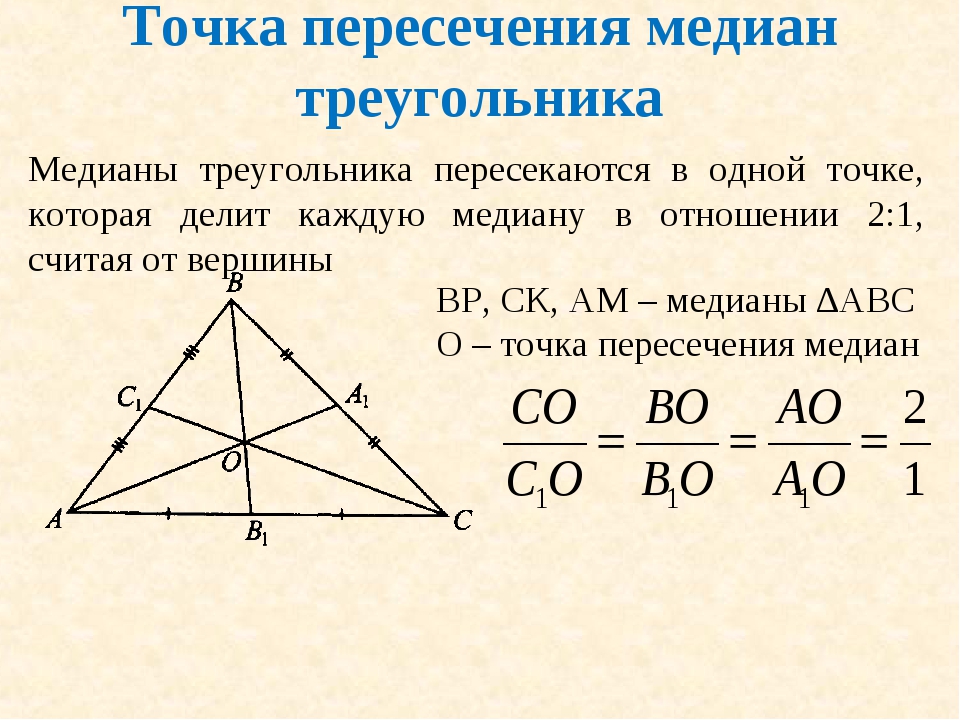
Для упрощения процесса используйте симметричные свойства треугольников, например, равенство сторон и углов.

Практика работы с координатами и геометрическими преобразованиями поможет быстрее освоить алгоритм нахождения вершин равностороннего треугольника на плоскости.

Определение натуральной величины треугольника АВС методом замены плоскостей проекции

Декартова система координат на плоскости