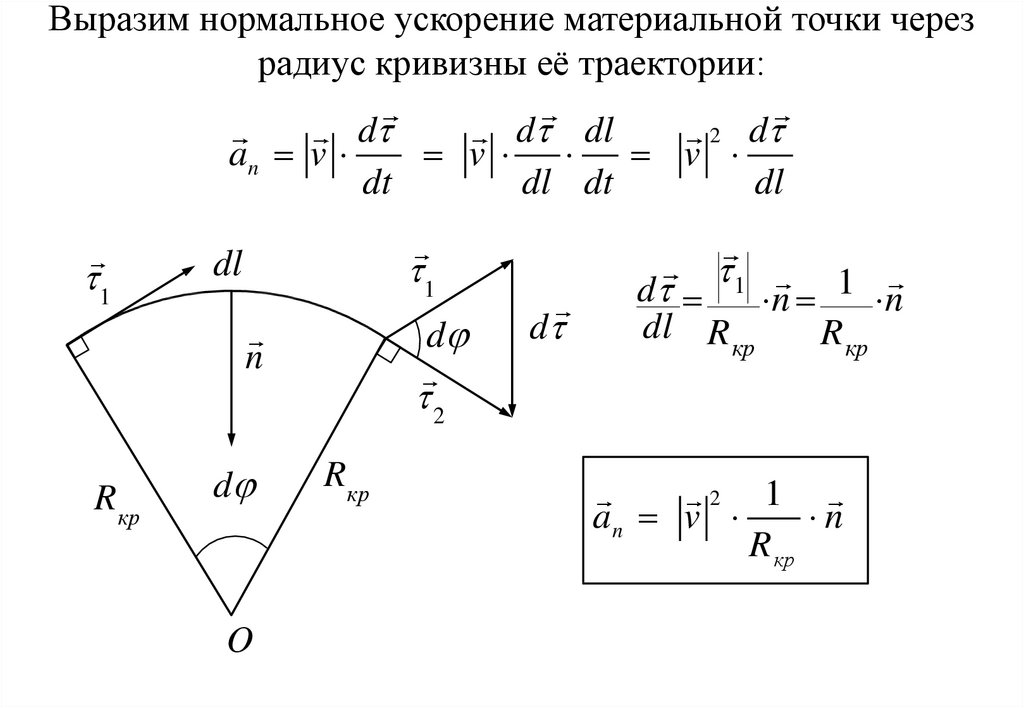
Как правильно вычислять касательное и нормальное ускорение: формулы и практическое применение
Этот материал познакомит вас с теорией касательного и нормального ускорения, объяснит основные формулы и методы их применения в различных физических задачах. Мы рассмотрим ключевые аспекты, которые помогут вам глубже понять процессы ускорения в движении объектов.
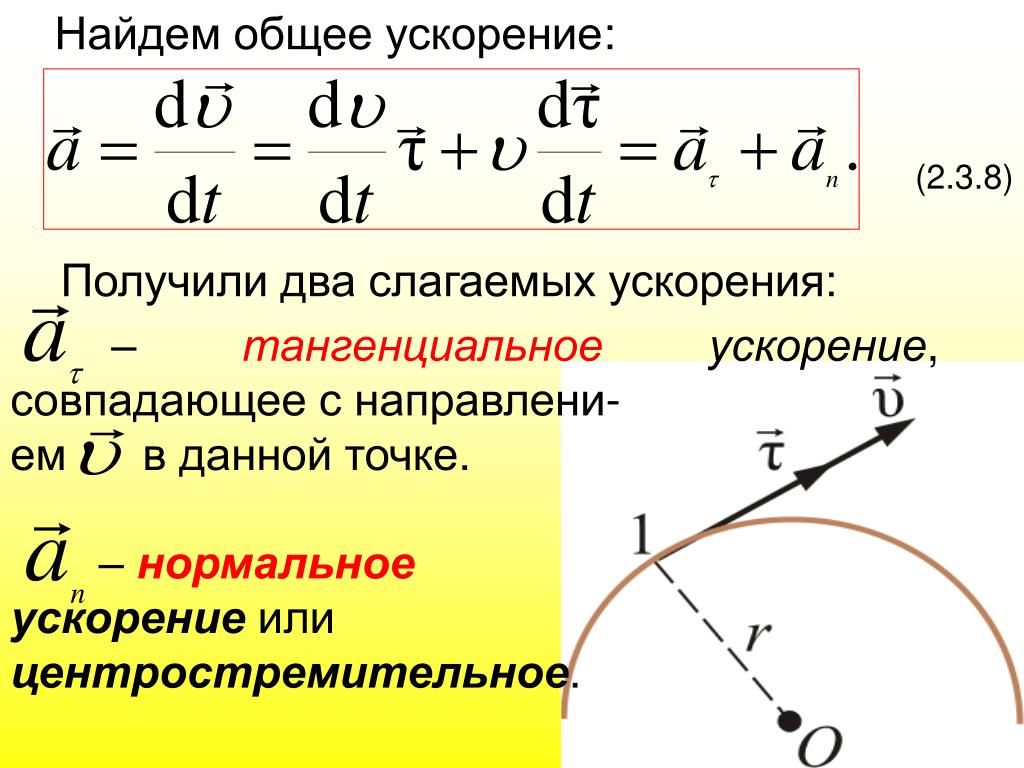

Для определения касательного ускорения используйте формулу a_t = dv/dt, где v — скорость объекта, а t — время.
Рассмотрение темы: \

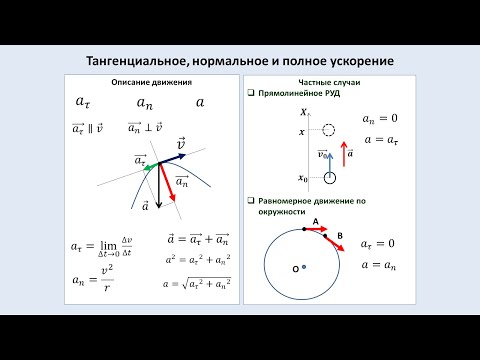
Нормальное ускорение можно найти через формулу a_n = v^2 / r, где v — скорость, а r — радиус кривизны траектории.

Лекция 6.5 - Нормальное и тангенциальное ускорение - Александр Чирцов - Лекториум
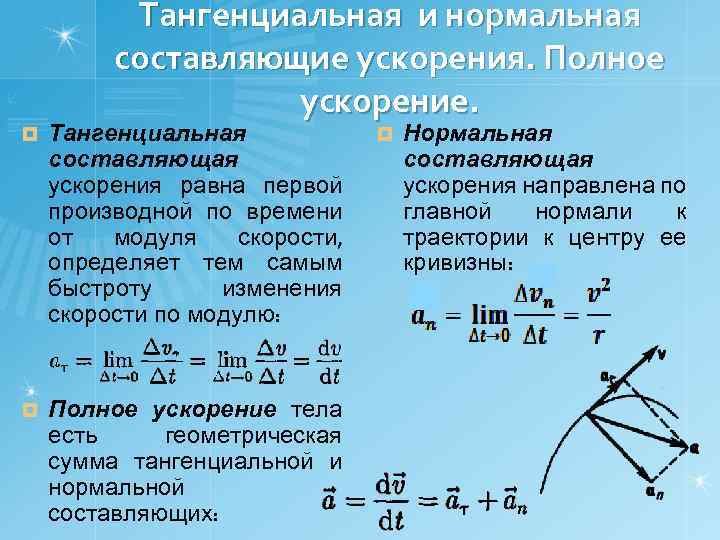

При движении по окружности, касательное и нормальное ускорение могут быть связаны через полный ускорение: a = √(a_t^2 + a_n^2).

Движение по окружности. Нормальное и тангенциальное ускорение - 50 уроков физики (4/50)

Не забывайте, что касательное ускорение всегда направлено по касательной к траектории, а нормальное — перпендикулярно.

Коэффициент мощности (cos φ) Активная, реактивная и полная мощность. Как исправить плохой коэфицент.
Для решения задач с ускорением полезно помнить, что касательное ускорение связано с изменением скорости по направлению движения, а нормальное — с изменением направления скорости.
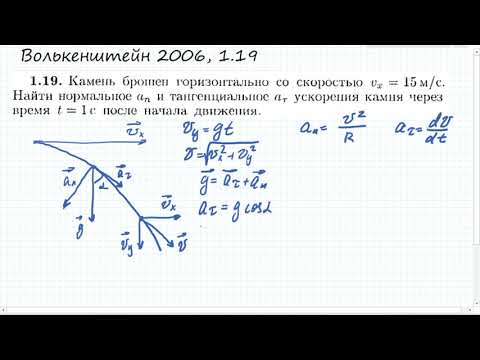
Хитрый способ нахождения тангенциального и нормального ускорений: Волькенштейн 1.19
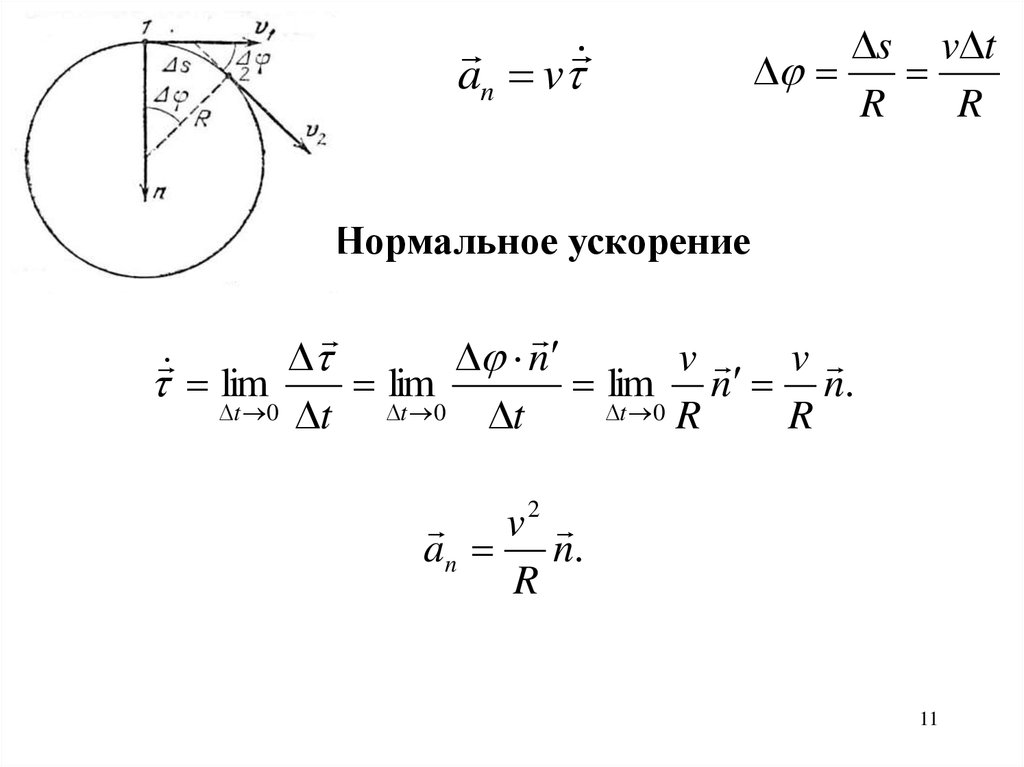
Если движение осуществляется по окружности, нормальное ускорение всегда направлено к центру окружности, что важно учитывать при решении задач.

Вращение по окружности, нормальное ускорение


Для определения величины ускорений в задачах часто необходимо вычислять радиус кривизны, что требует дополнительных геометрических знаний.

2.5. Векторные формулы для скоростей и ускорений

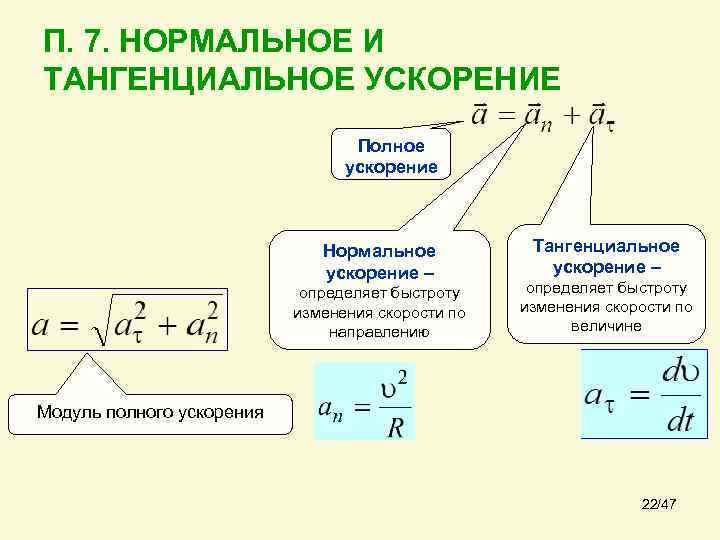
В задачах на движение по кривой важно не только рассчитать ускорения, но и учитывать их взаимное влияние на результат.

Скорости и ускорения точек вращающегося тела

Центростремительное ускорение. 9 класс.
Когда задачи касаются движения в круге, важно правильно понимать разницу между линейной и угловой скоростью для правильного применения формул.

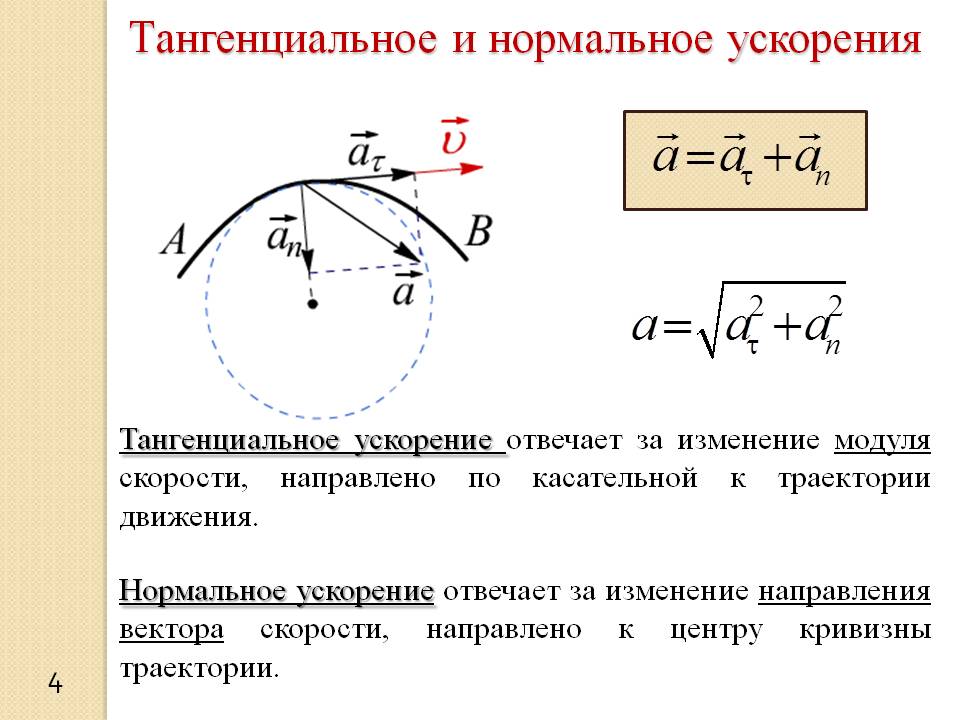
Для сложных траекторий с изменяющимися радиусами кривизны потребуется использовать более сложные методы анализа движения, такие как дифференциальные уравнения.

Построение планов ускорений. Абсолютное ускорение. Нормальное ускорение. Касательное ускорение.