Пошаговое руководство по созданию канонической системы координат для гиперболы
Этот материал поможет вам разобраться в принципах построения канонической системы координат для гиперболы, которая упрощает анализ и решение задач. Мы расскажем о ключевых аспектах, которые нужно учитывать, и предложим полезные советы для работы с гиперболами в различных контекстах.

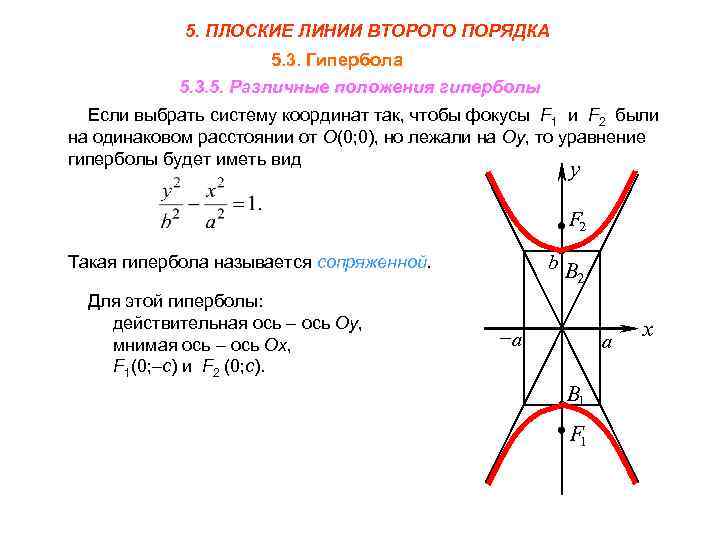
Для начала важно понять, что каноническая система координат для гиперболы основывается на использовании осей, перпендикулярных друг другу, с фокусами на главной оси.

§31.1 Приведение уравнения кривой к каноническому виду
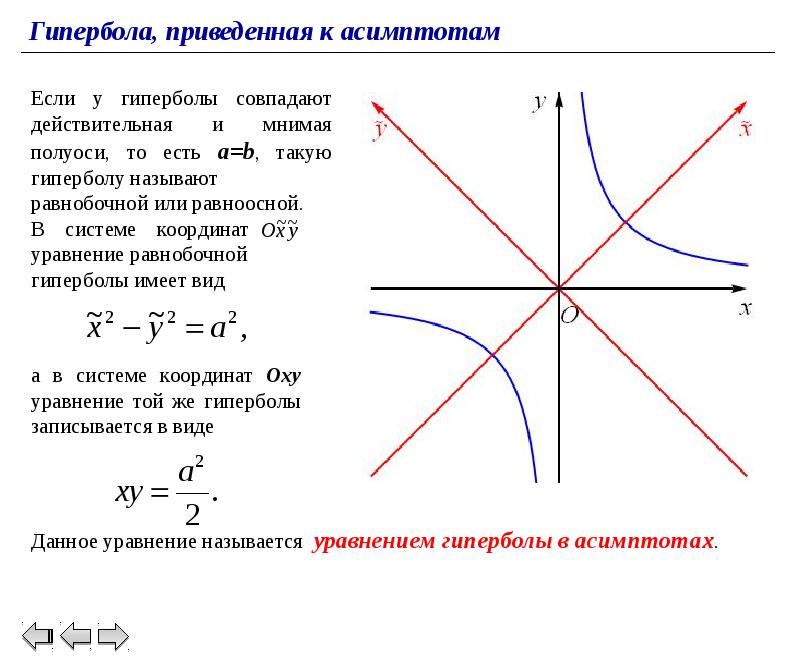

Преимущество канонической формы заключается в том, что уравнение гиперболы становится гораздо проще и легче поддается анализу.
§21 Каноническое уравнение гиперболы
Не забывайте, что в канонической системе координат гипербола имеет два фокуса, и расстояние между ними определяет основные характеристики кривой.

Кривые второго порядка. Гипербола. Приведение к каноническому виду и чертеж
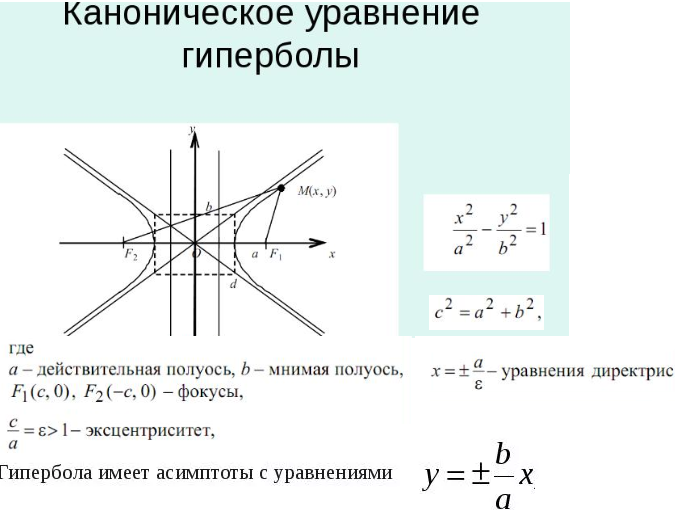

Важно правильно выбрать положение гиперболы относительно координатных осей для минимизации вычислительных ошибок и упрощения решения задач.
функция y=k/x и ее график (гипербола) - 8 класс алгебра
При переходе к канонической форме гиперболы важно уметь правильно использовать стандартные уравнения, такие как (x²/a²) - (y²/b²) = 1 для гиперболы с горизонтальной осью.
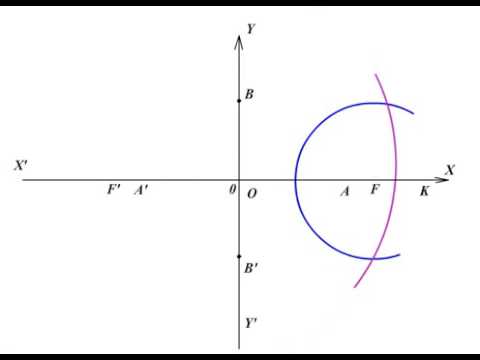
Построение гиперболы

Определите, какой вид гиперболы вам нужен (горизонтальная или вертикальная), так как от этого зависит форма канонического уравнения.

Гипербола. (Аналитическая геометрия - урок 10)

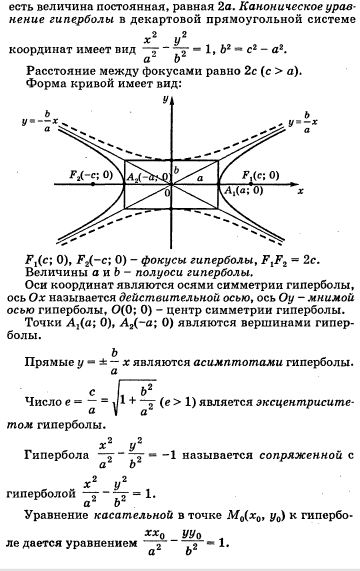
Для гиперболы, имеющей вертикальную ось, уравнение будет выглядеть как (y²/a²) - (x²/b²) = 1, что также важно учитывать при переходе к канонической форме.


При изменении координатных осей старайтесь сохранять пропорции, чтобы правильно отразить характеристики гиперболы в новой системе координат.
Используйте диаграммы и графики, чтобы визуализировать преобразования и лучше понять структуру гиперболы в канонической системе координат.

Применяйте методы оптимизации при решении задач, связанных с гиперболами, чтобы повысить точность расчетов и сократить время на выполнение вычислений.
