Методы нахождения производной по графику функции и касательной к ней

В этой статье мы рассмотрим, как можно определить производную функции, анализируя её график и касательную прямую. Такие методы особенно полезны для визуального восприятия производных, а также в случае, если аналитическое выражение функции неизвестно. Мы дадим практические советы, которые помогут вам правильно вычислить производную, используя графические подходы.

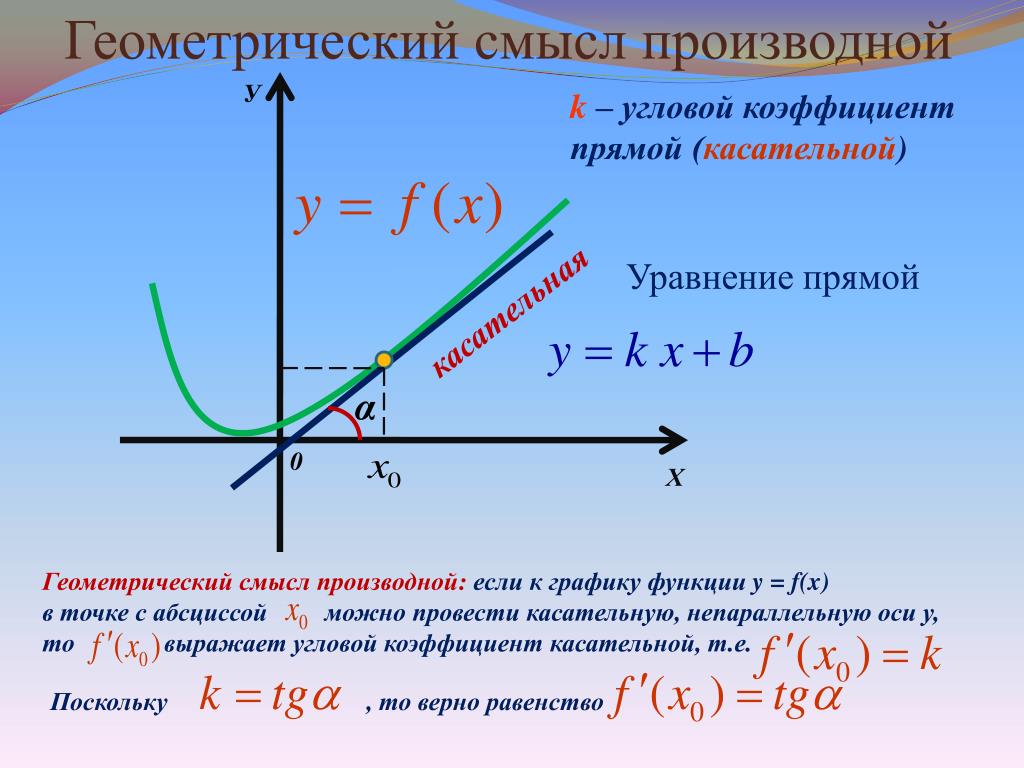
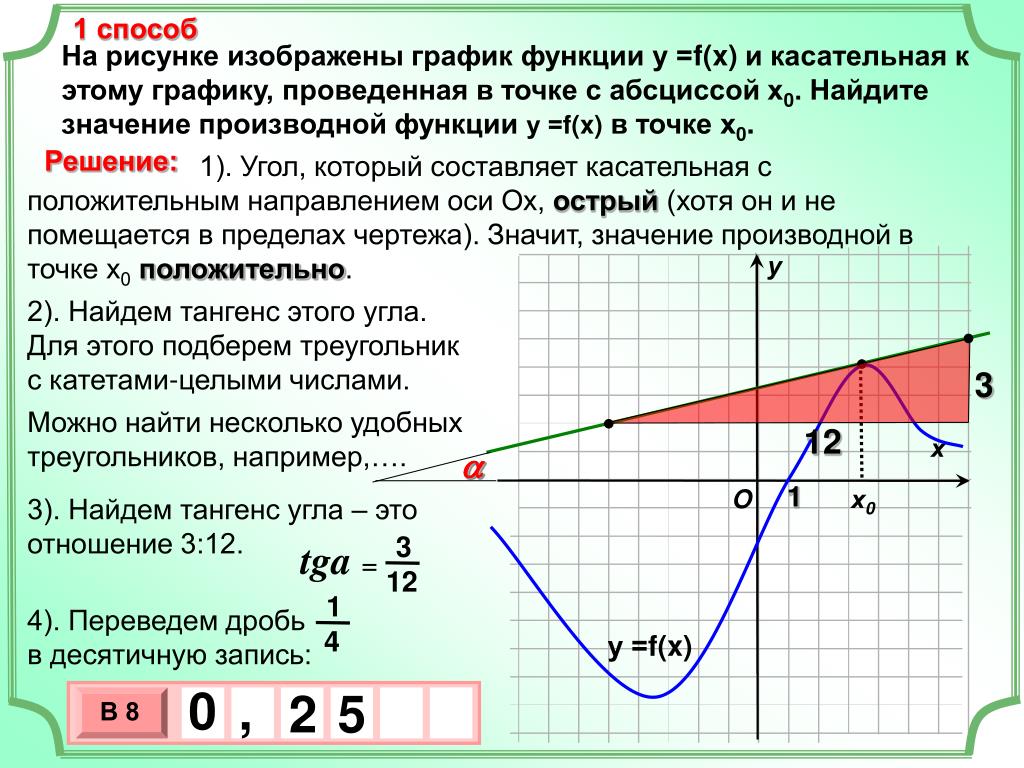
При анализе графика функции для нахождения производной ориентируйтесь на угловой коэффициент касательной к графику в нужной точке.

Запомните, что касательная прямая к графику функции в точке имеет такой же наклон, как и сама производная функции в этой точке.

Если график функции имеет резкие углы или разрывы, то в этих точках производная может быть несуществующей.

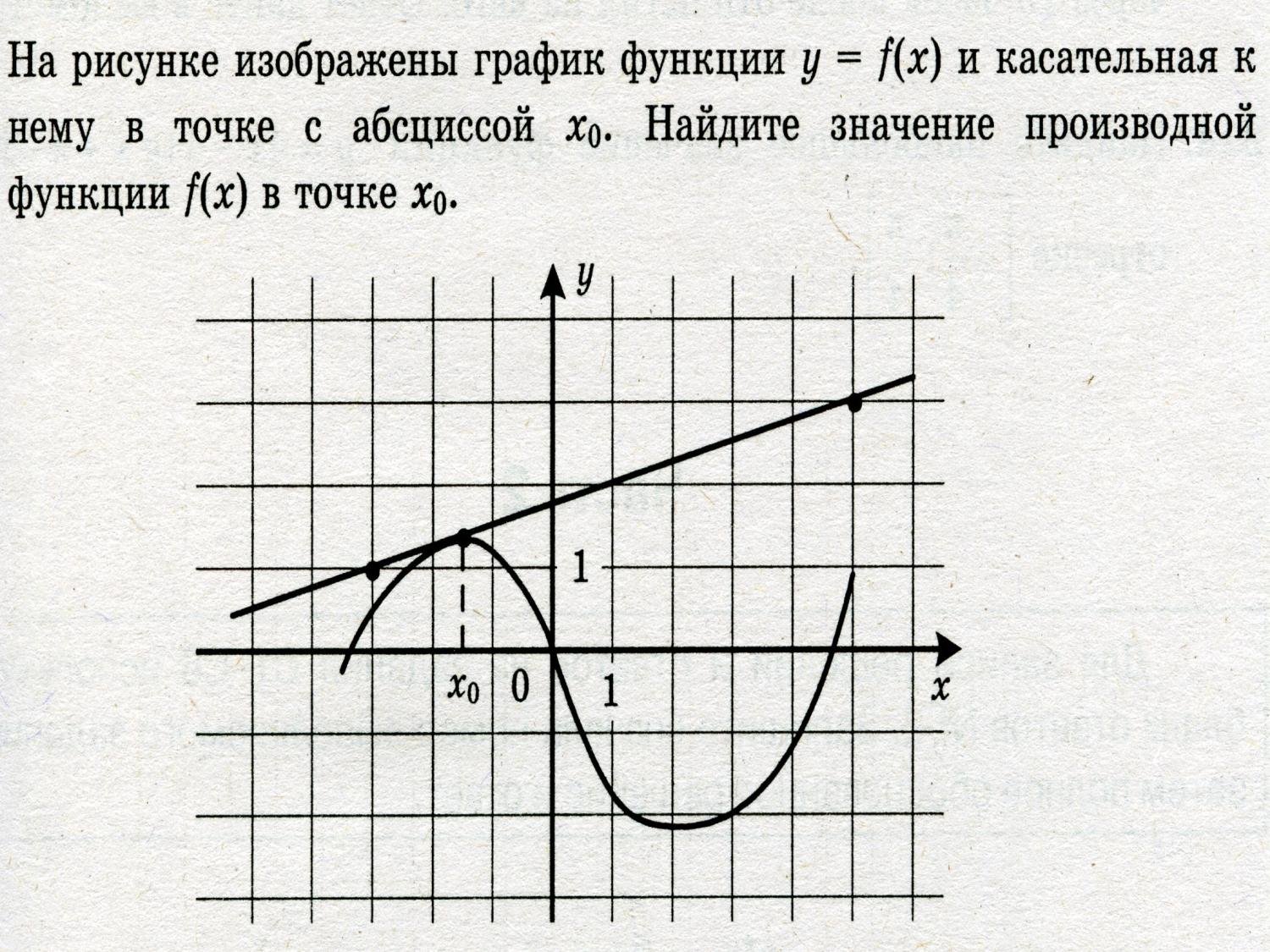
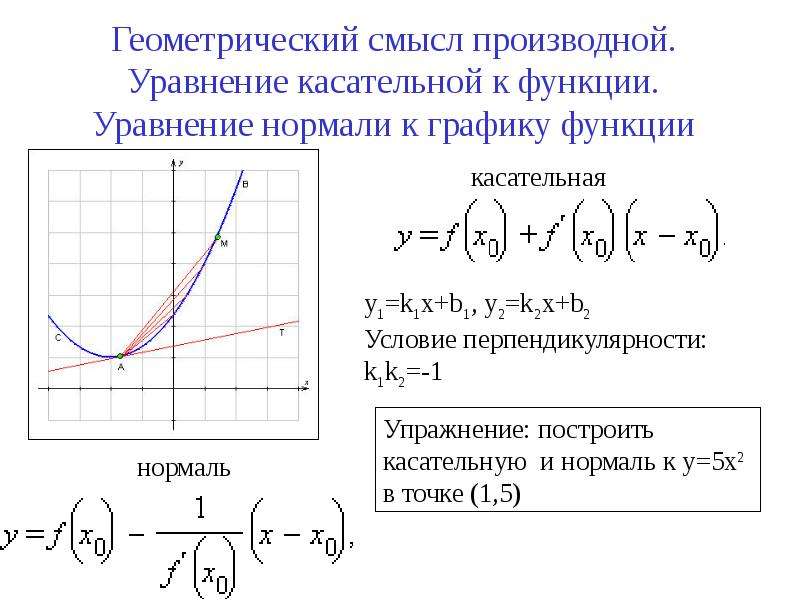
Для нахождения производной по графику обращайте внимание на моменты, где график функции резко изменяет направление — это признаки локальных экстремумов.

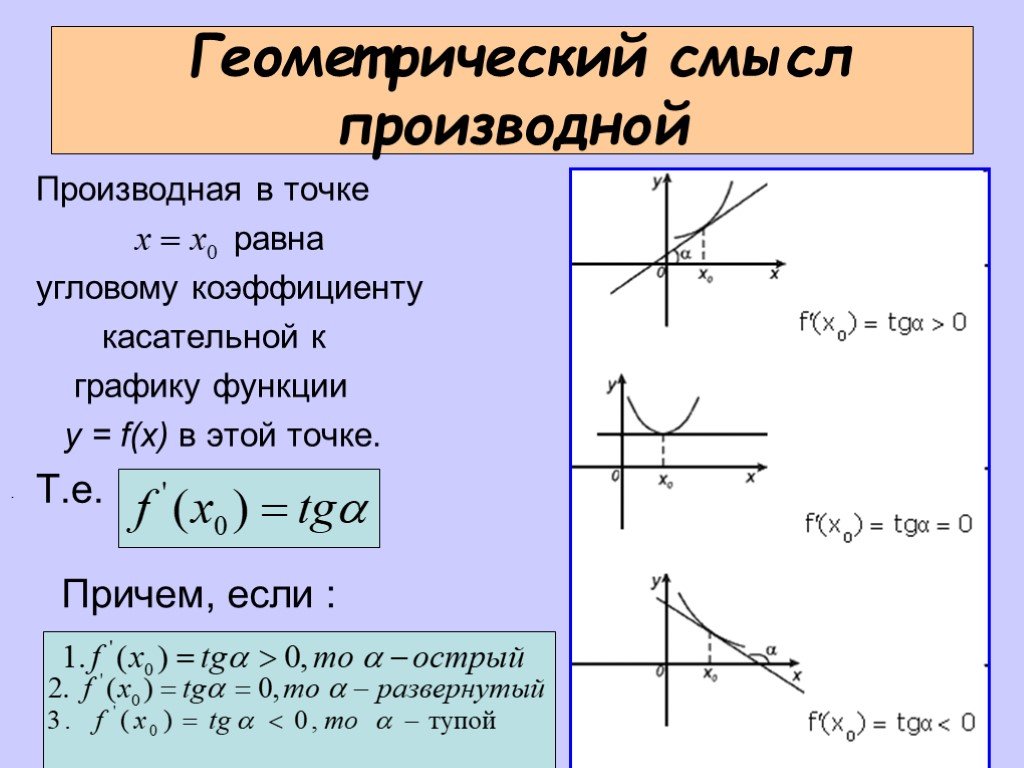
На участке, где график функции возрастает, производная будет положительной, а на убывающем участке — отрицательной.

Используйте касательную для точного определения наклона функции в каждой точке. Чем ближе точка, тем точнее будет определение производной.

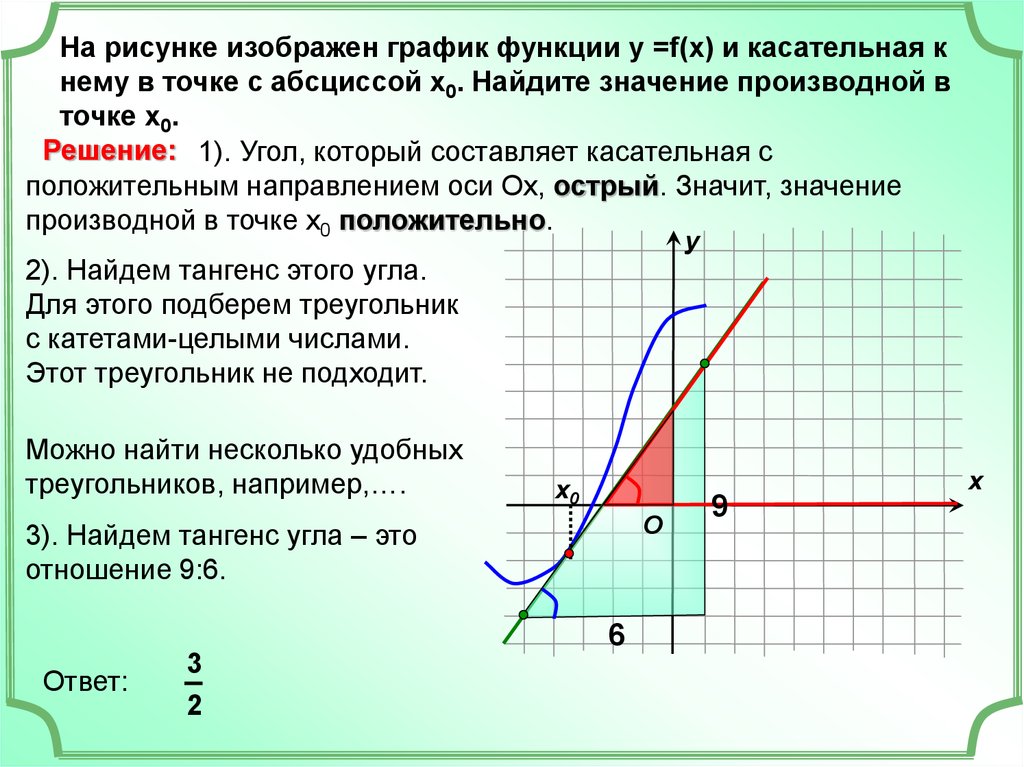
Если касательная прямая горизонтальна, это означает, что производная в этой точке равна нулю.

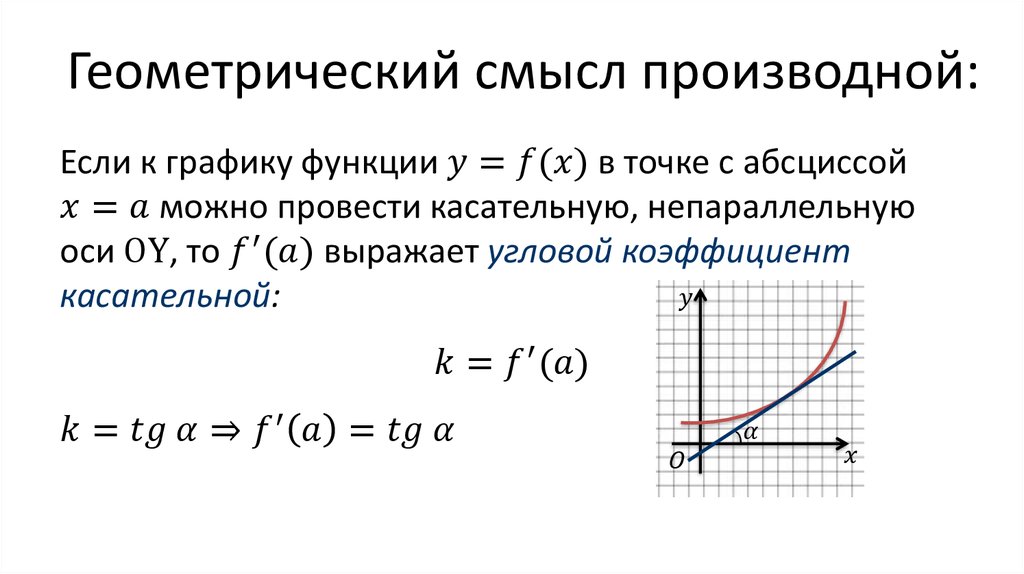
Для более точных вычислений производной можно воспользоваться программами или графическими калькуляторами, которые позволят получить более точные данные о наклоне касательной.

Обратите внимание, что на графике функции непрерывной и гладкой производная существует в каждой точке, где можно провести касательную прямую.

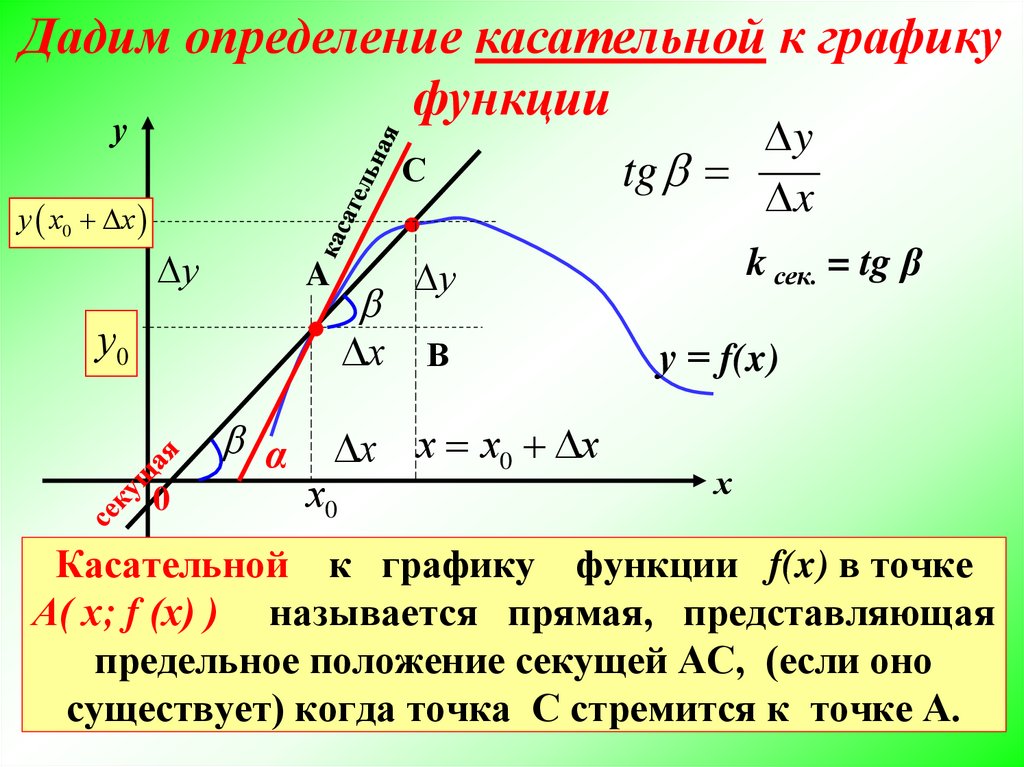
Если график функции имеет плавный изгиб, то производная в этой точке будет конечной и равна угловому коэффициенту касательной, проведенной в данной точке.