Методы нахождения производной функции по графику на практике
На этой странице вы найдете советы и методы для нахождения значения производной функции, используя её график. Мы рассмотрим, как визуально определить наклон касательной и что он означает для производной в данной точке.

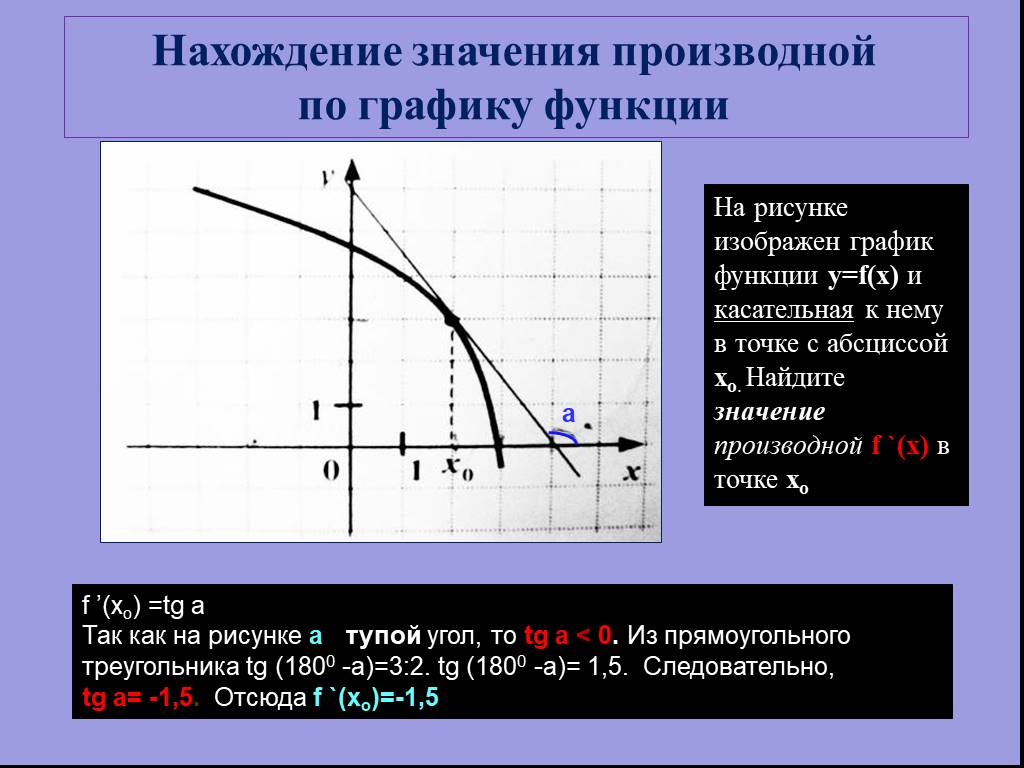
Для нахождения производной по графику функции используйте касательную к графику в точке, где нужно найти производную.

Производная: секретные методы решения. Готовимся к ЕГЭ - Математика TutorOnline
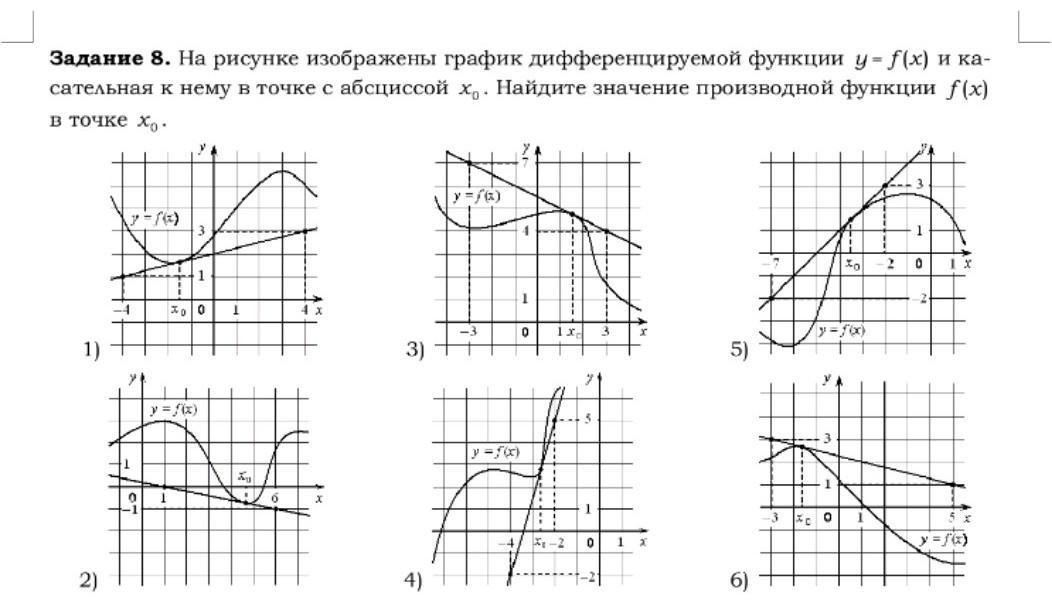
Производная функции в точке равна угловому коэффициенту касательной, проведённой к графику функции в этой точке.
Производная функции. 10 класс.
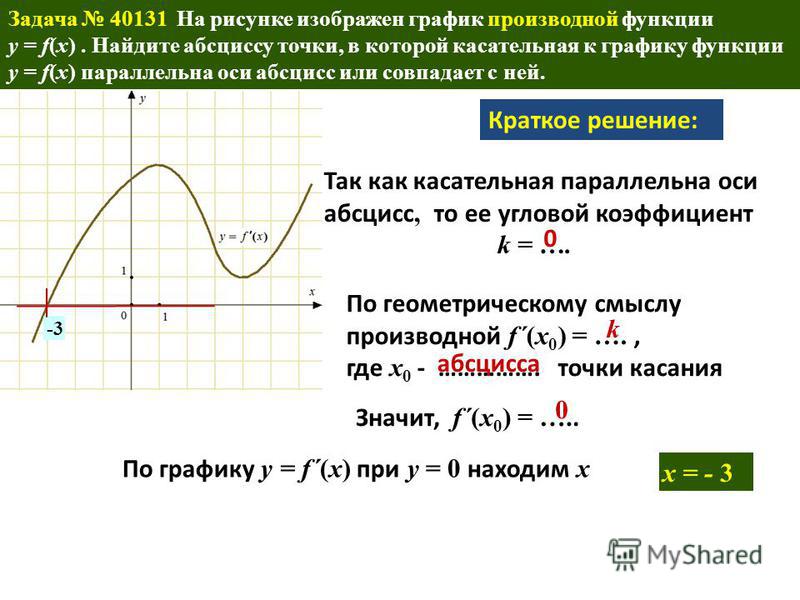
Если график функции имеет вертикальную касательную, то производная в этой точке не существует.

Этой задачей русские дети 10 лет мучили американцев. Американцы не понимали, что делают не так
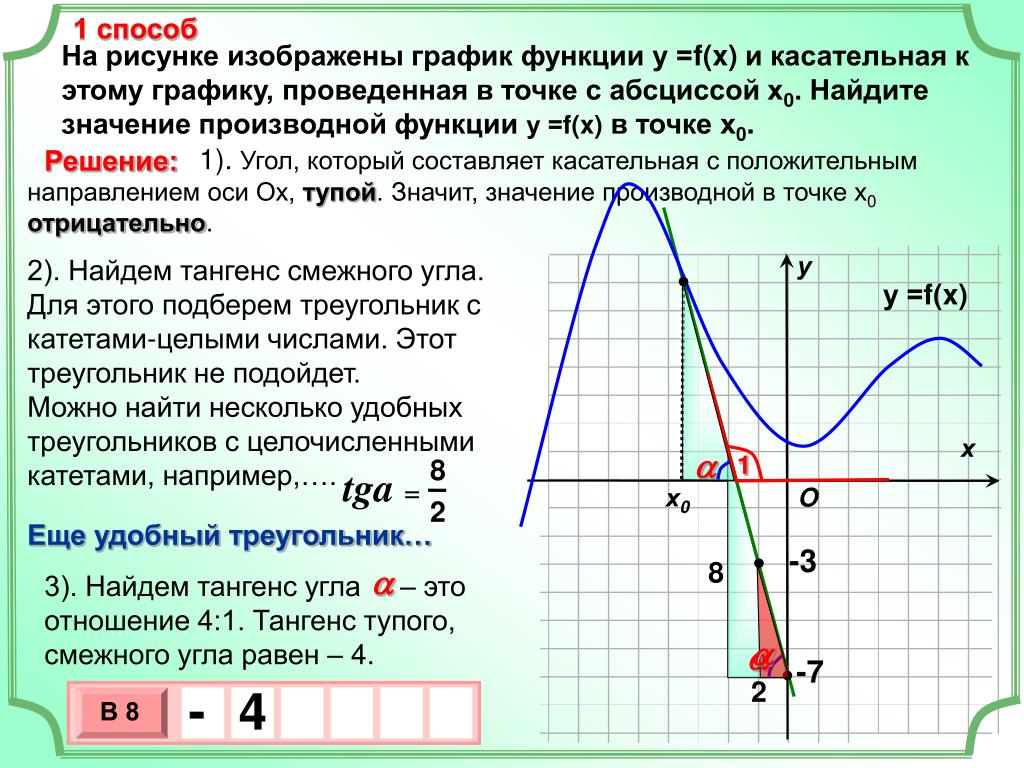
Обратите внимание на направление касательной: если она направлена вверх, производная положительна, если вниз — отрицательна.

ПРОИЗВОДНАЯ функции. Объяснение математического смысла.
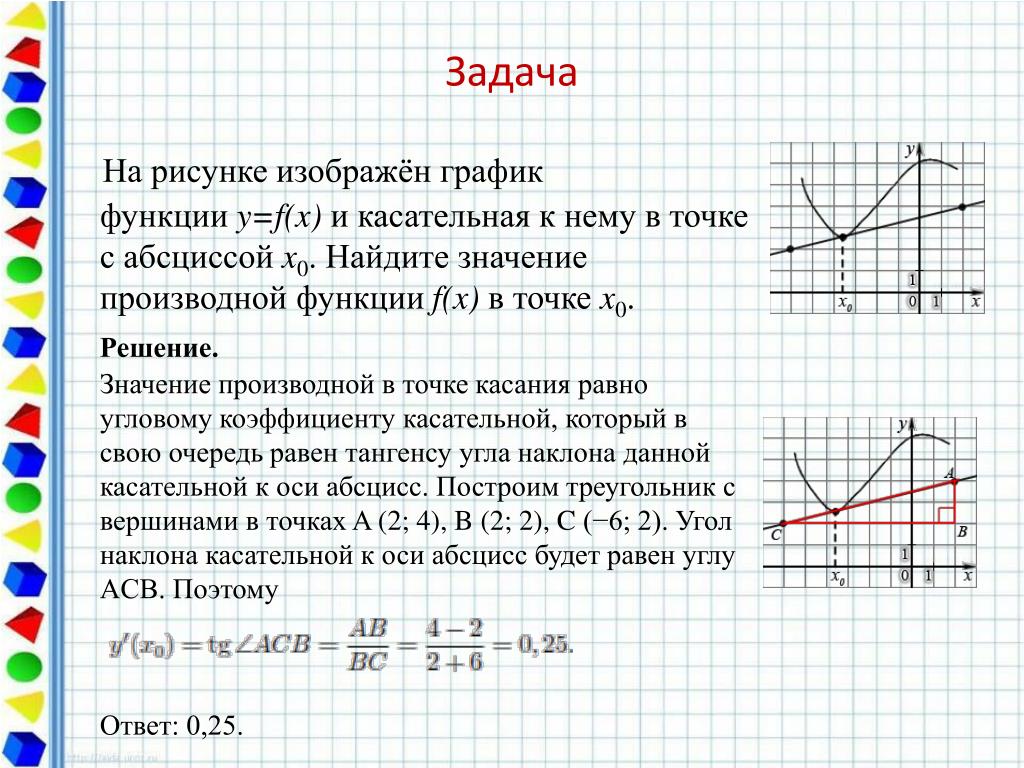
Чтобы точно определить производную, проведите касательную и посчитайте её угловой коэффициент с помощью известных точек.

Геометрический смысл производной - Касательная
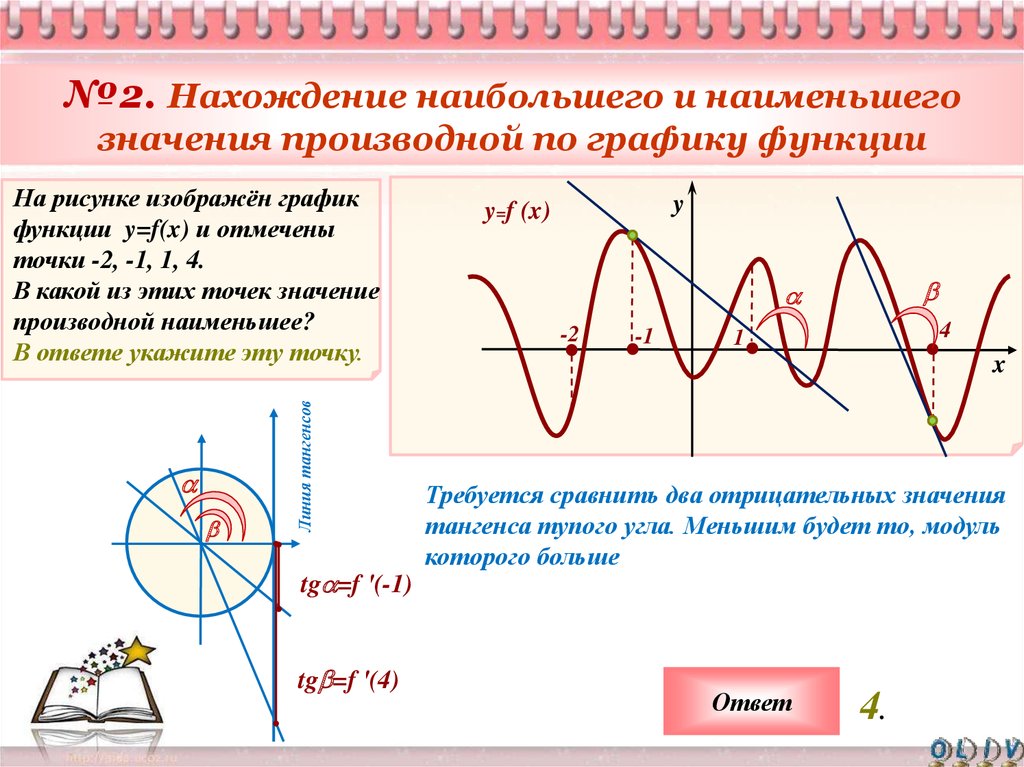
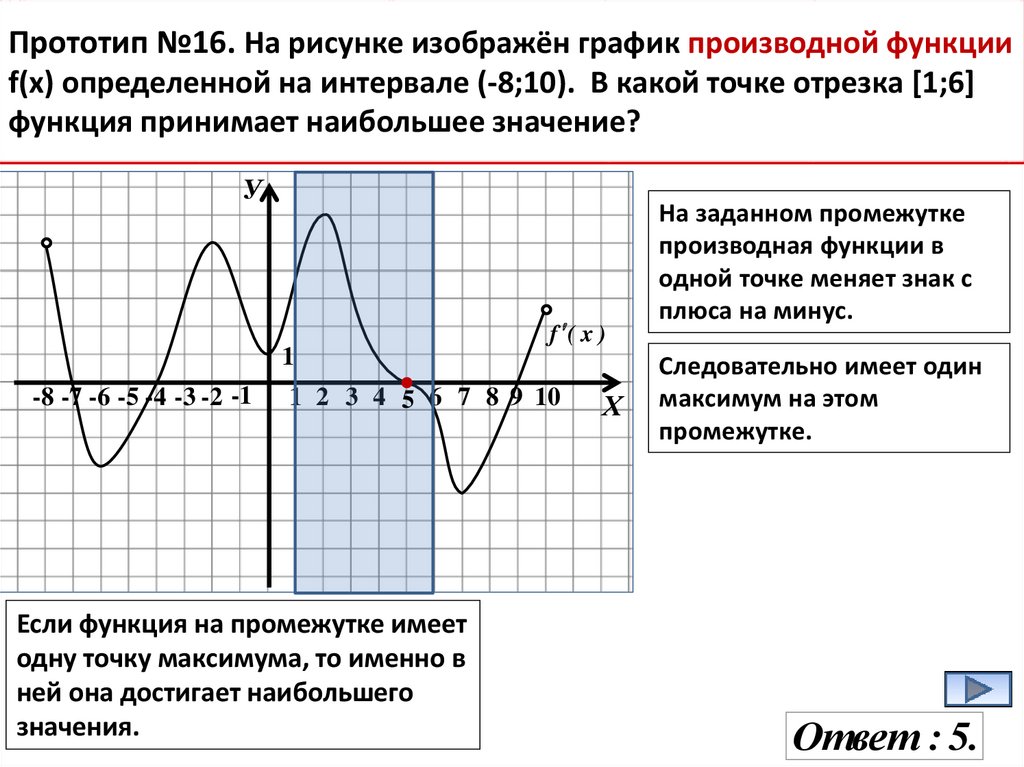
Если график функции представляет собой кривую, постарайтесь найти точку, где касательная линия ровно горизонтальна — это означает, что производная равна нулю.
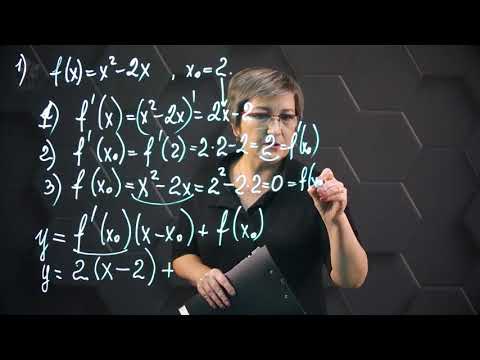
Уравнение касательной в точке. Практическая часть. 1ч. 10 класс.
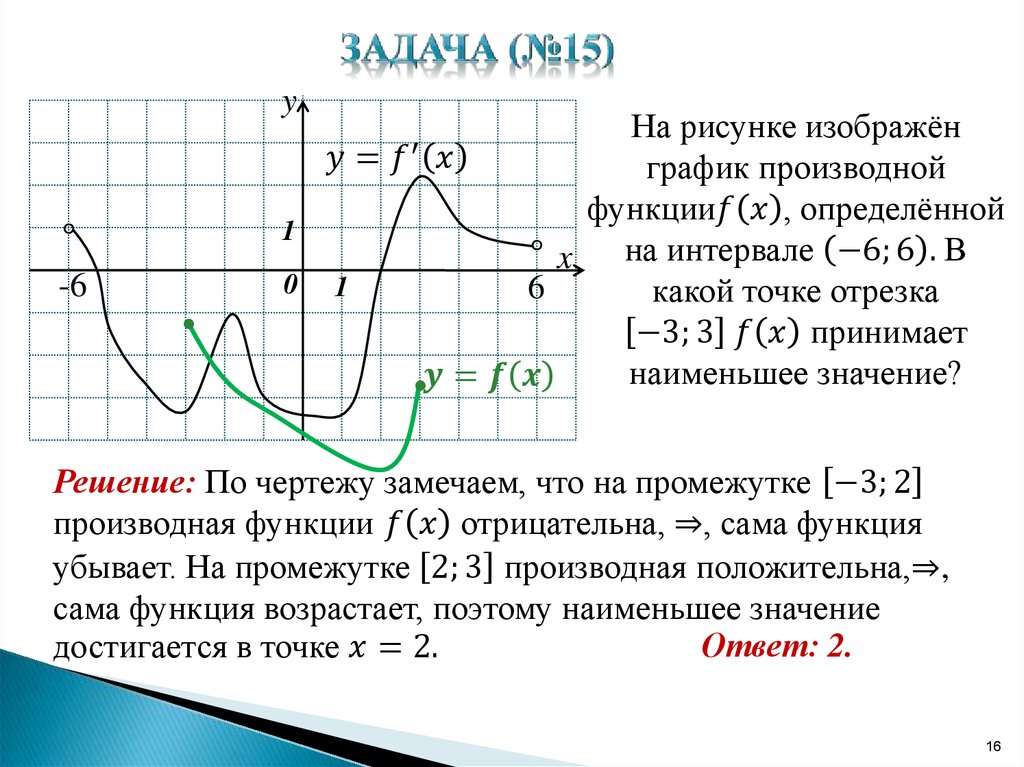
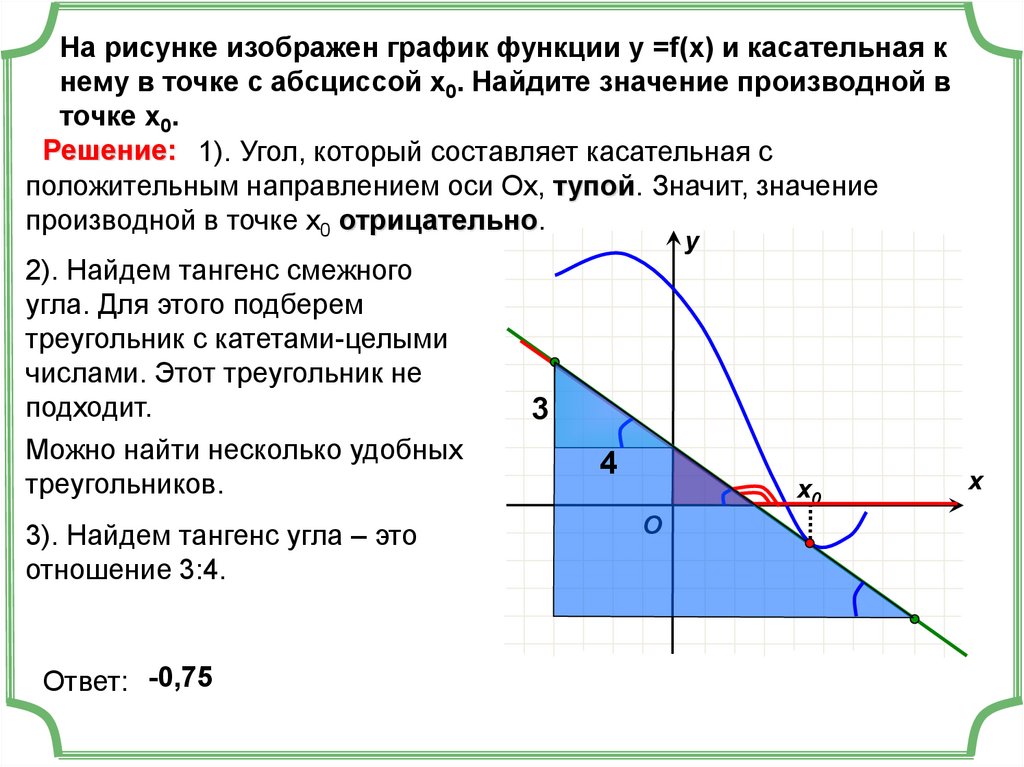
Для графиков, имеющих резкие углы, не забывайте, что производная может не существовать в этих точках.
Используйте увеличение графика в нужной точке, чтобы точнее определить угол наклона касательной и вычислить производную.
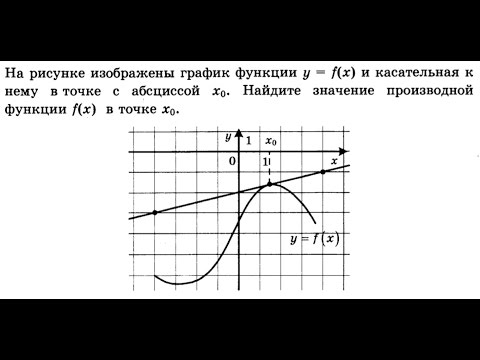
ЕГЭ 2017 Профильный №7 найти производную в точке касания #7
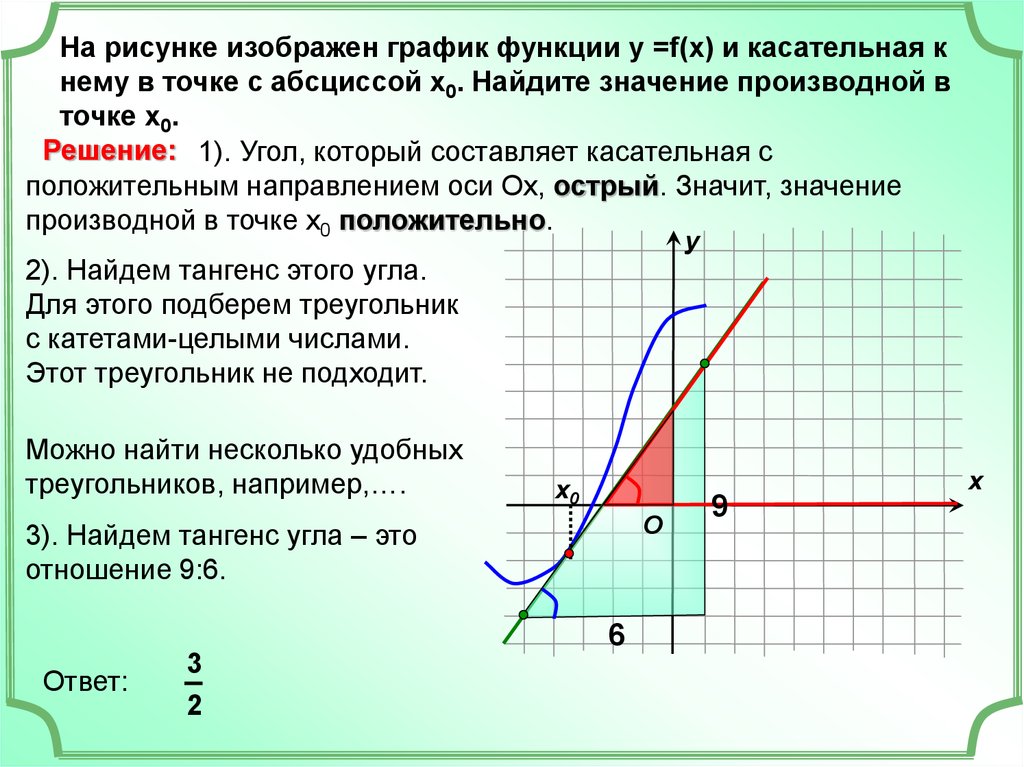
Внимательно наблюдайте за поведением графика функции: если он имеет горизонтальный участок, то на этом участке производная равна нулю.
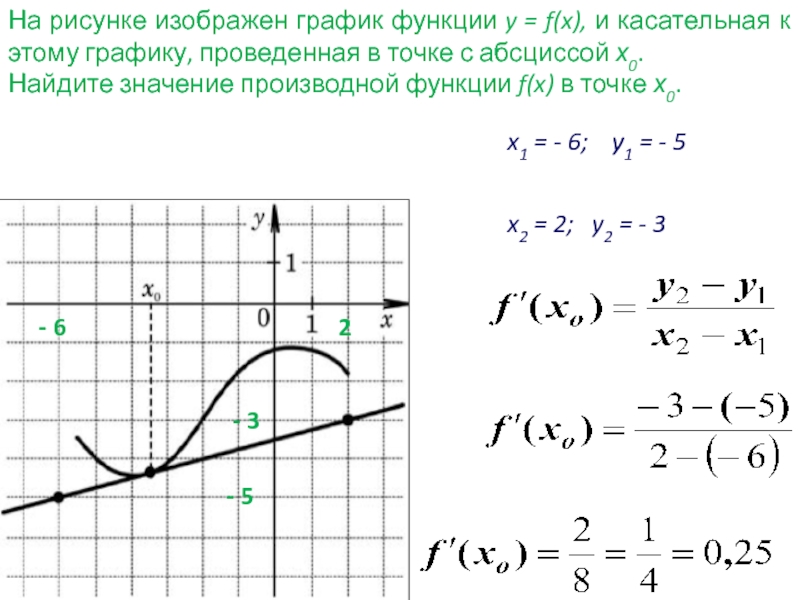
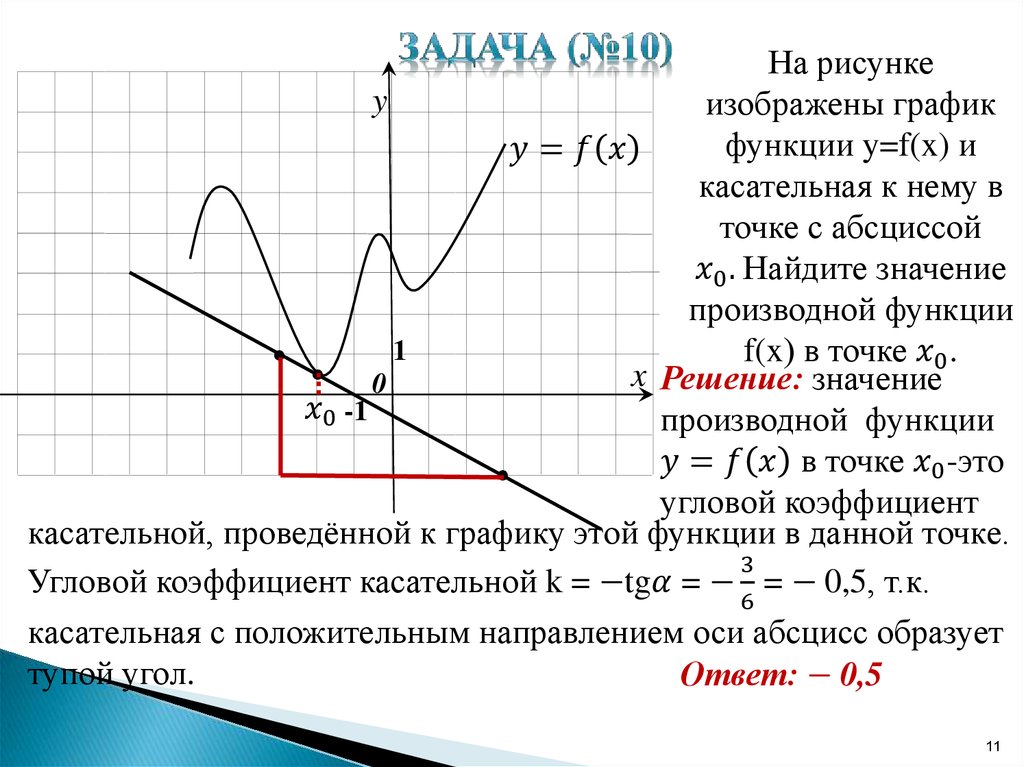
Чем более плавным и линейным является участок графика, тем проще точно найти производную, так как угловой коэффициент касательной будет постоянным.
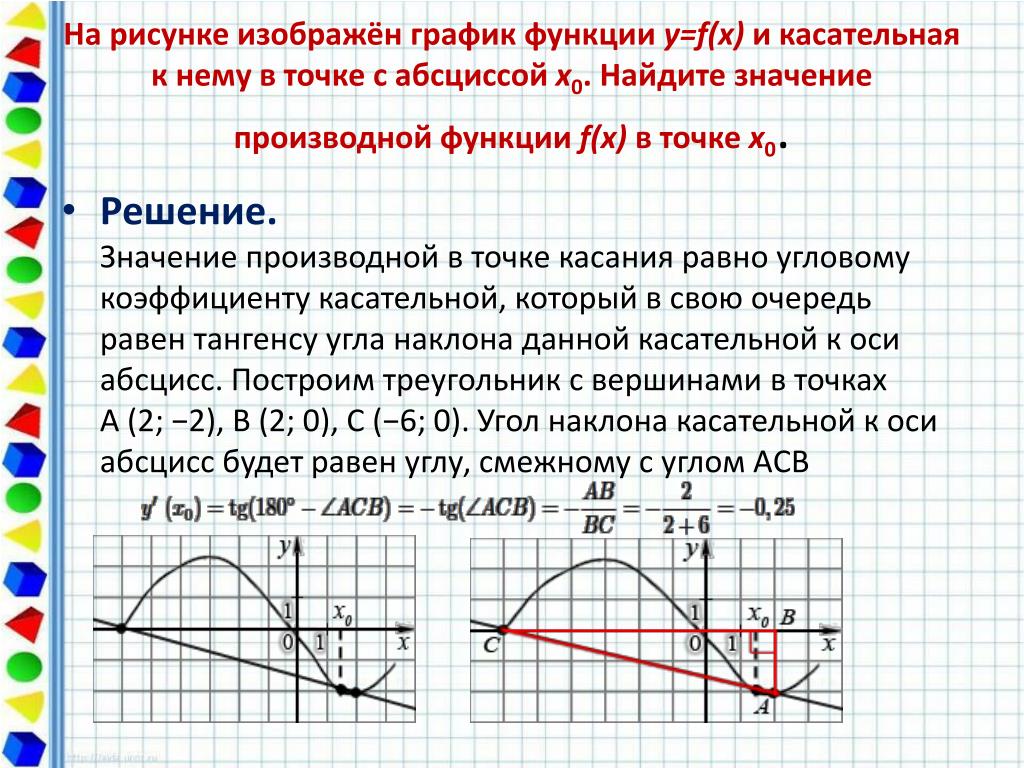
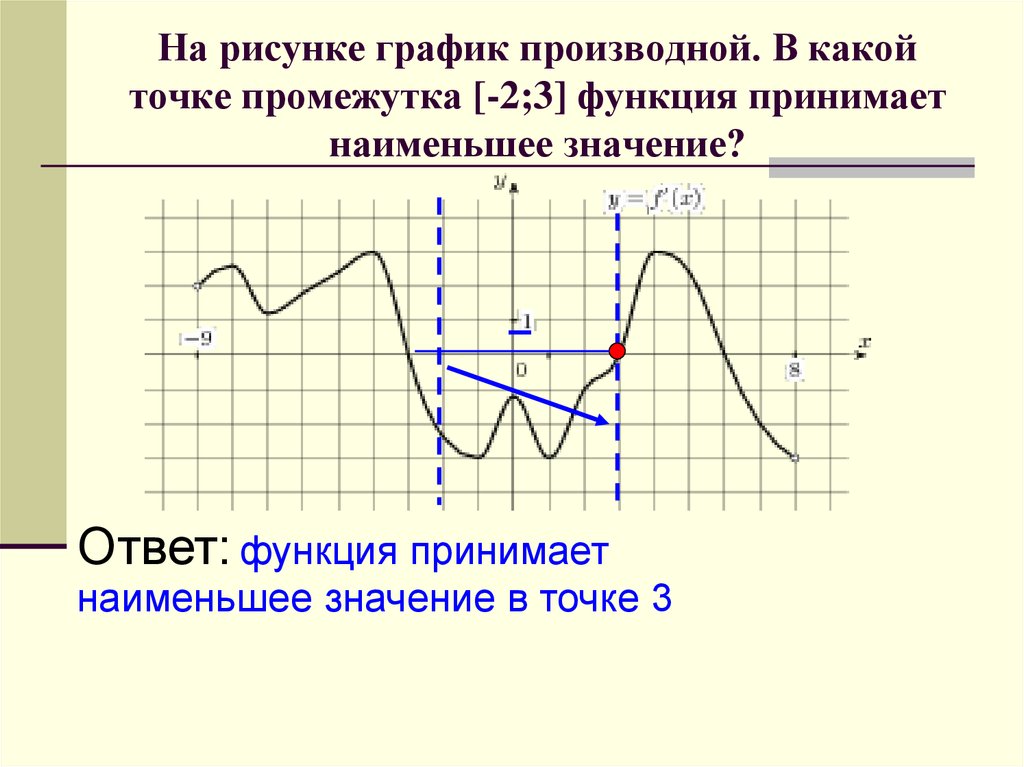
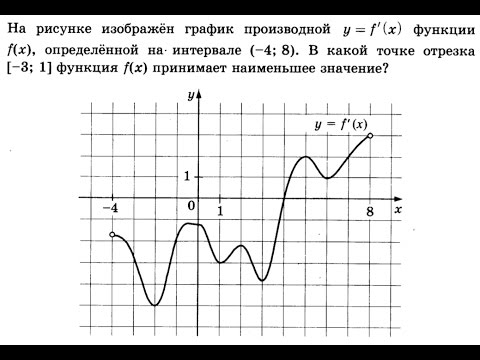
ЕГЭ 2017 Профильный №7 есть график производной, найти где функция минимальна #7