Шаги и методы нахождения алгебраического дополнения для матрицы
Алгебраическое дополнение матрицы — это важная концепция линейной алгебры, которая используется при вычислении определителей и инверсии матриц. Знание того, как его найти, необходимо для решения многих задач в математике и инженерии. В этом разделе мы разберем основные шаги и методы для нахождения алгебраического дополнения матрицы, а также дадим полезные советы и примеры.


Для нахождения алгебраического дополнения необходимо вычислить минора для каждой позиции элемента в матрице, а затем умножить его на знак, который зависит от положения элемента в матрице.

Видеоурок \

Не забывайте, что алгебраическое дополнение используется в расчетах определителей и для нахождения обратной матрицы. Это важный инструмент для более глубокого понимания свойств матриц.

Как найти алгебраическое дополнение?
Если матрица является квадратной, то алгебраическое дополнение для каждого элемента можно вычислить через минора, который получается после удаления соответствующей строки и столбца.
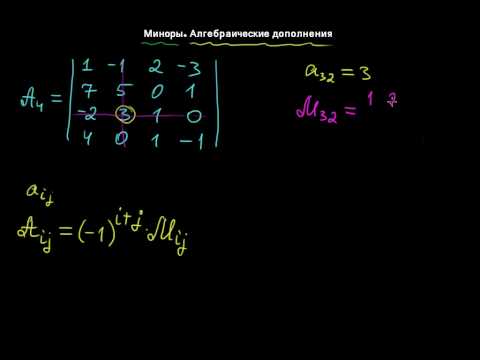
§12 Миноры. Алгебраические дополнения

Для начала практики рекомендуется использовать небольшие матрицы (например, 3x3), чтобы проще понять процесс вычислений и увидеть закономерности.

Дополнительные миноры и алгебраические дополнения. Тема
Внимательно следите за знаками при вычислениях. Они зависят от положения элемента в матрице: знак равен (+) или (-) в зависимости от четности суммы индексов строки и столбца элемента.

Урок 2. Обратная матрица: метод Гаусса, алгебраическое дополнение - Высшая математика - TutorOnline

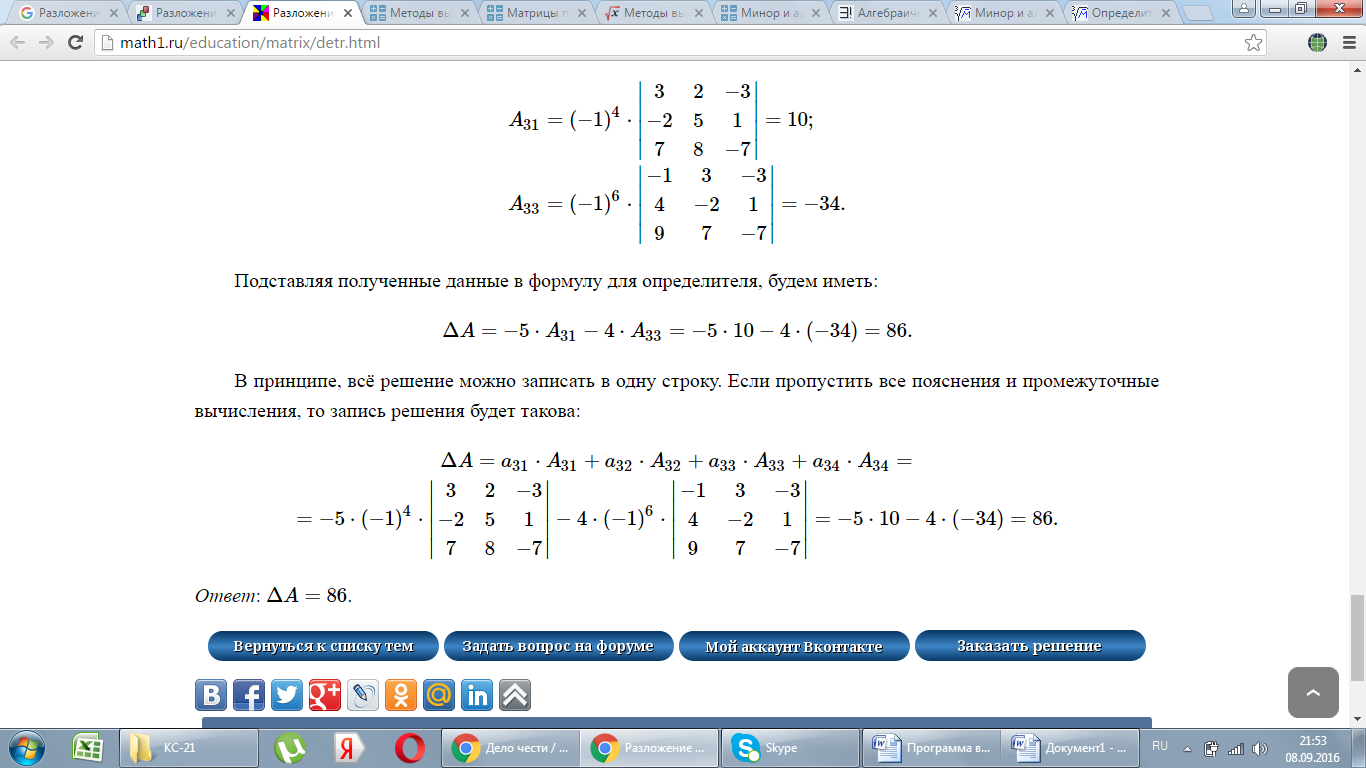
Алгебраическое дополнение важно не только для теории, но и для численных методов, таких как решение систем линейных уравнений и нахождение инверсии матрицы.


Попробуйте использовать программное обеспечение или калькуляторы для проверки ваших вычислений. Это поможет быстрее и точнее понять, где могли возникнуть ошибки.

8. Обратная матрица

При работе с большими матрицами для вычисления алгебраического дополнения можно использовать метод разложения по строкам или столбцам, чтобы упростить процесс нахождения миноров.
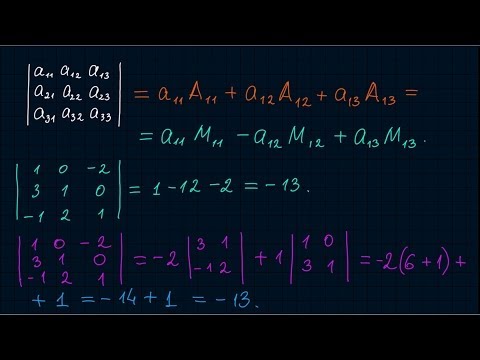
Миноры и алгебраические дополнения

Алгебраические дополнения матрицы
Для лучшего запоминания принципов нахождения алгебраического дополнения полезно провести несколько примеров с разными размерами матриц.


Если возникают трудности с определением минора, попробуйте сначала выписать его элементы в виде меньшей матрицы, исключив соответствующую строку и столбец.

ОПРЕДЕЛИТЕЛЬ МАТРИЦЫ 2х2 3х3 4x4 свойства определителя
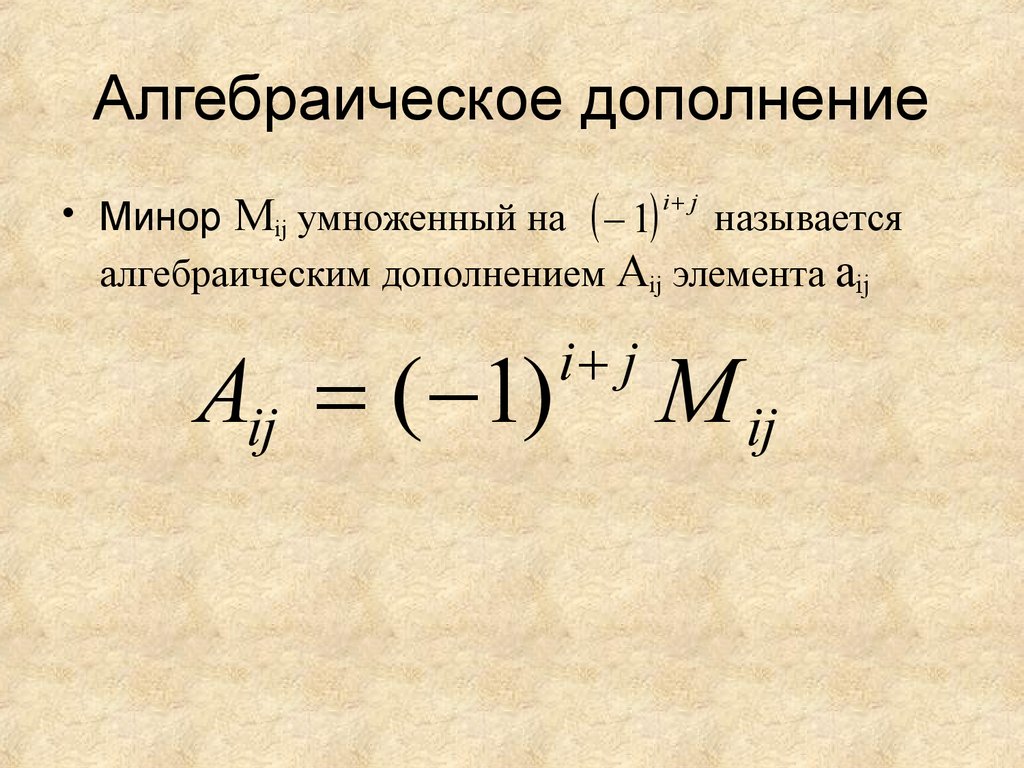

Минор и алгебраическое дополнение матрицы как найти, решение примера