Графики периодических функций: основные особенности и советы для начинающих
На этой странице вы найдете полезные советы и примеры графиков периодических функций, которые помогут вам лучше понять и запомнить основные принципы их построения. Мы расскажем, как правильно анализировать периодичность, амплитуду и фазовый сдвиг таких функций, а также представим практические советы по их графическому изображению.

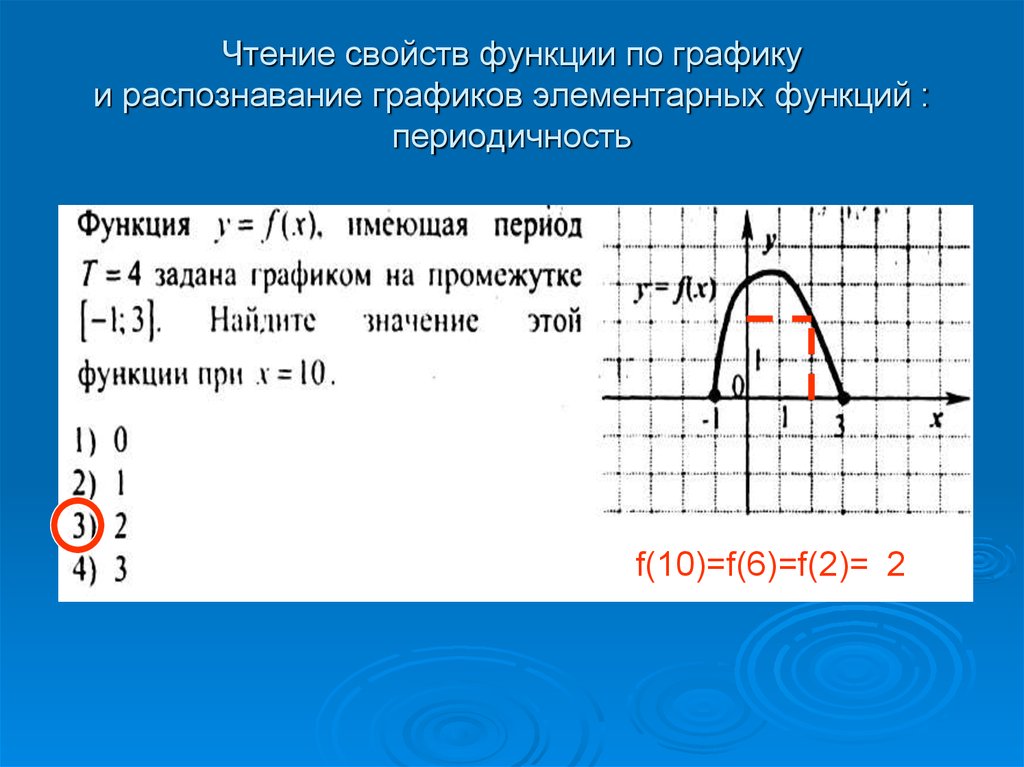
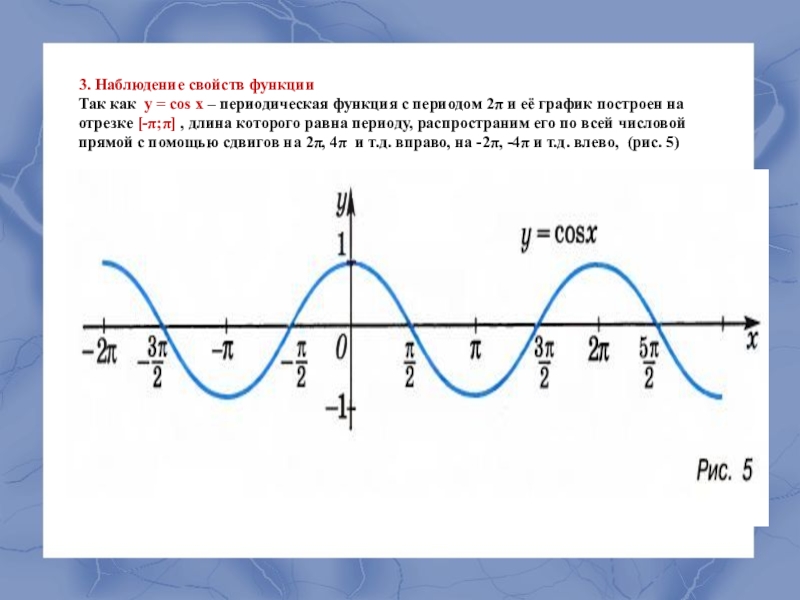
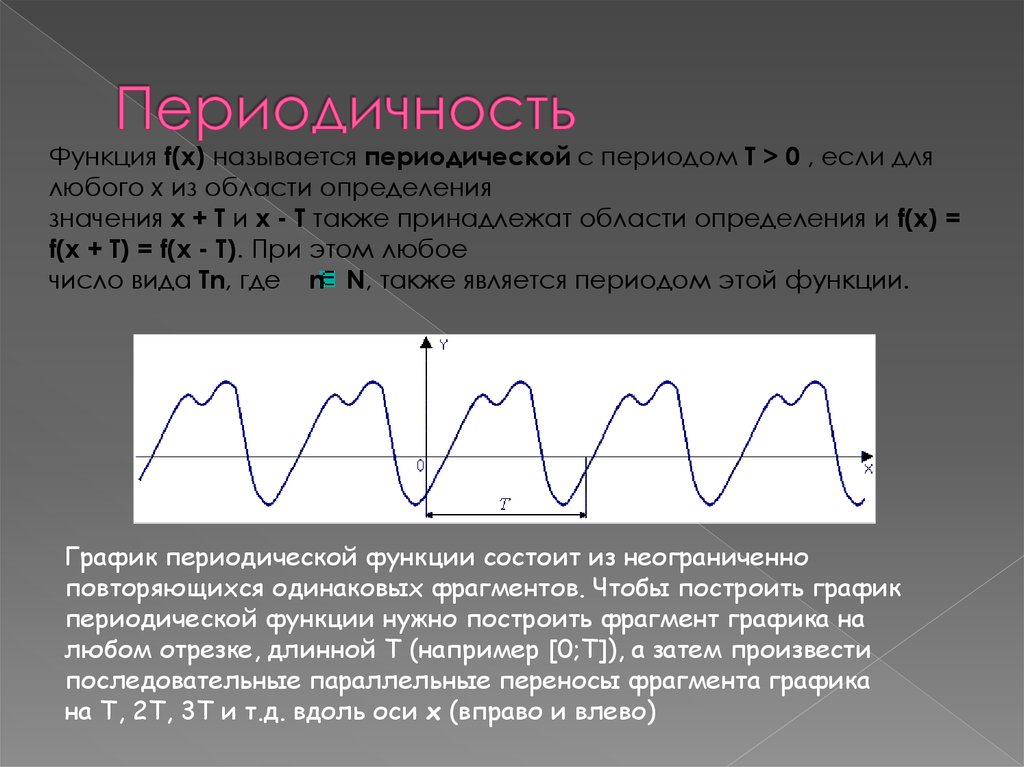
Для начала определите период функции, чтобы понять, через сколько единиц повторяется ее график.

10 класс, 9 урок, Периодические функции
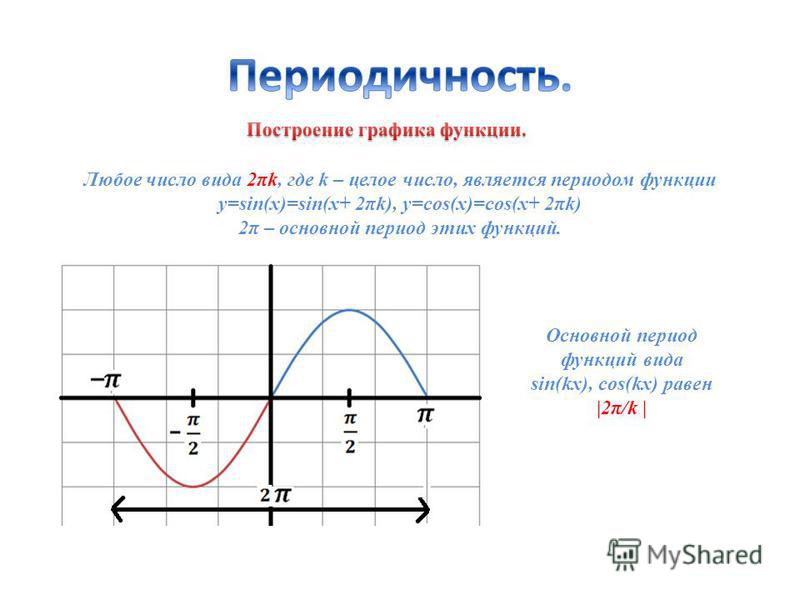

Запомните, что амплитуда графика влияет на его высоту и низ, что важно для корректного изображения функции.

Графики параметрически и неявно заданных функций. Пределы на Тейлора и Лопиталя.
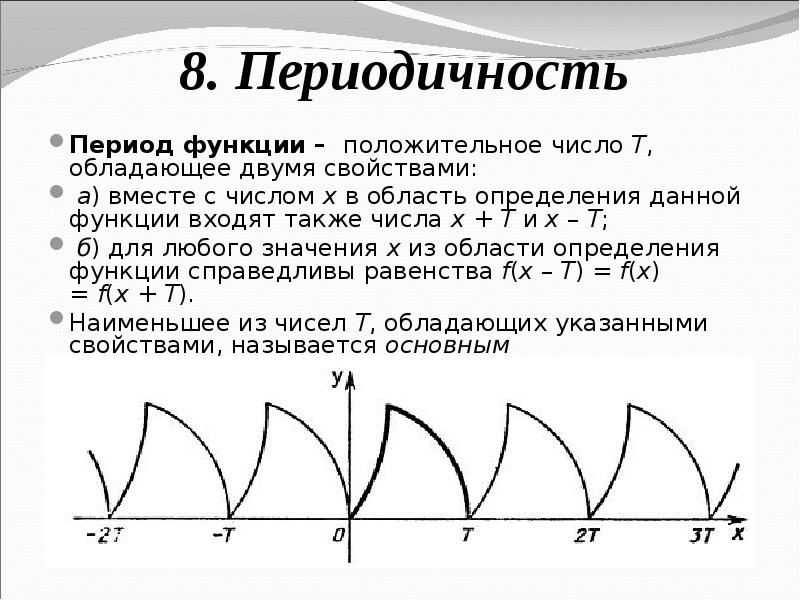
Используйте сетку для более точного отображения колебаний и изменений графика периодической функции.

Период функции #1
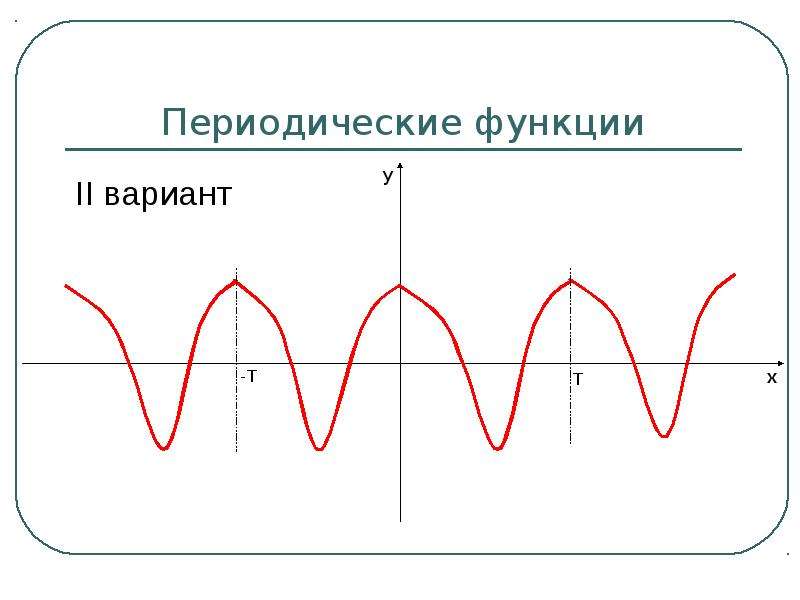
Учитывайте фазовый сдвиг: он отвечает за сдвиг графика по оси X влево или вправо.

Функция. Часть 4.1. Преобразование графиков
Графики синусоидальных и косинусоидальных функций схожи, но косинус сдвинут относительно синуса по фазе на 90 градусов.

Чтение графиков функций. Определение свойств функции по графику.
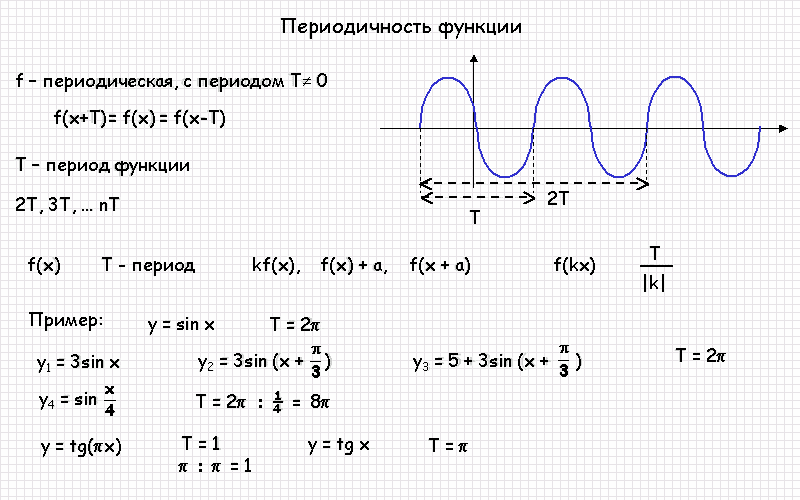
Если функция имеет дополнительные множители, такие как коэффициенты перед аргументом, они могут изменять период или амплитуду графика.
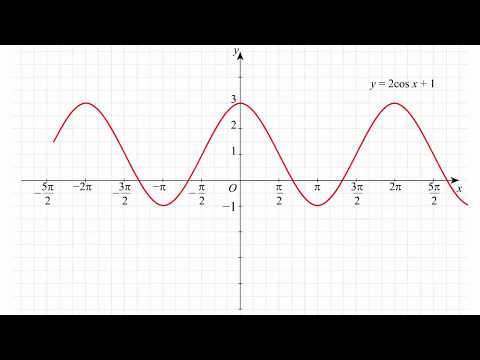
Построение графика функции y=2cos(x)+1
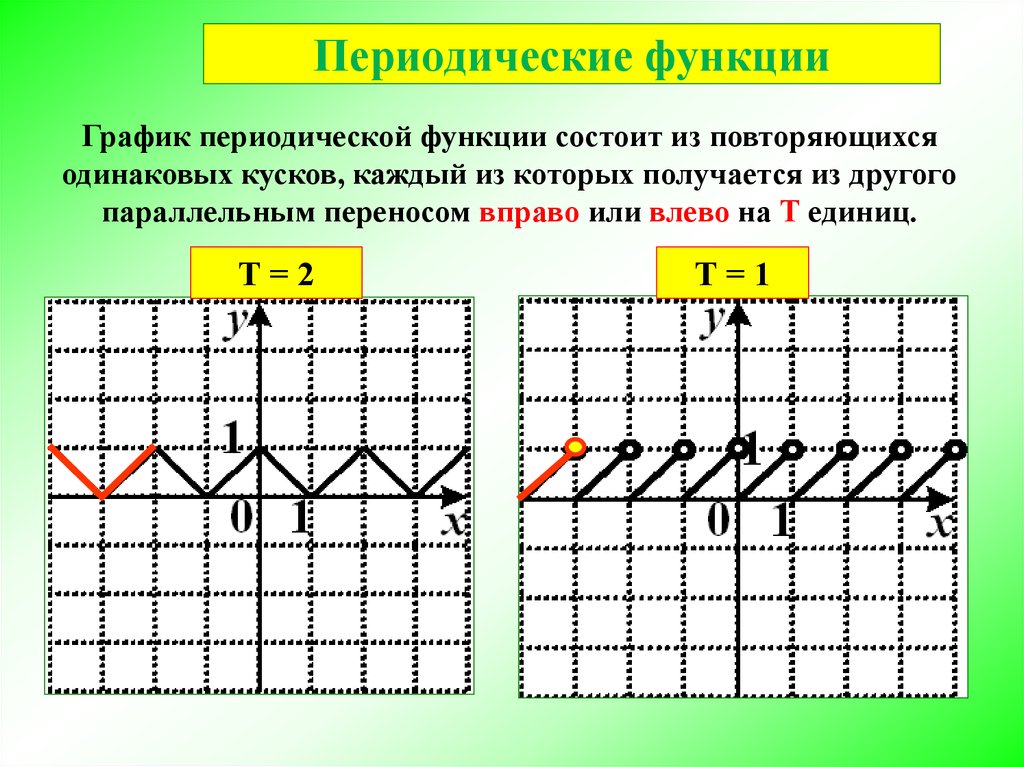
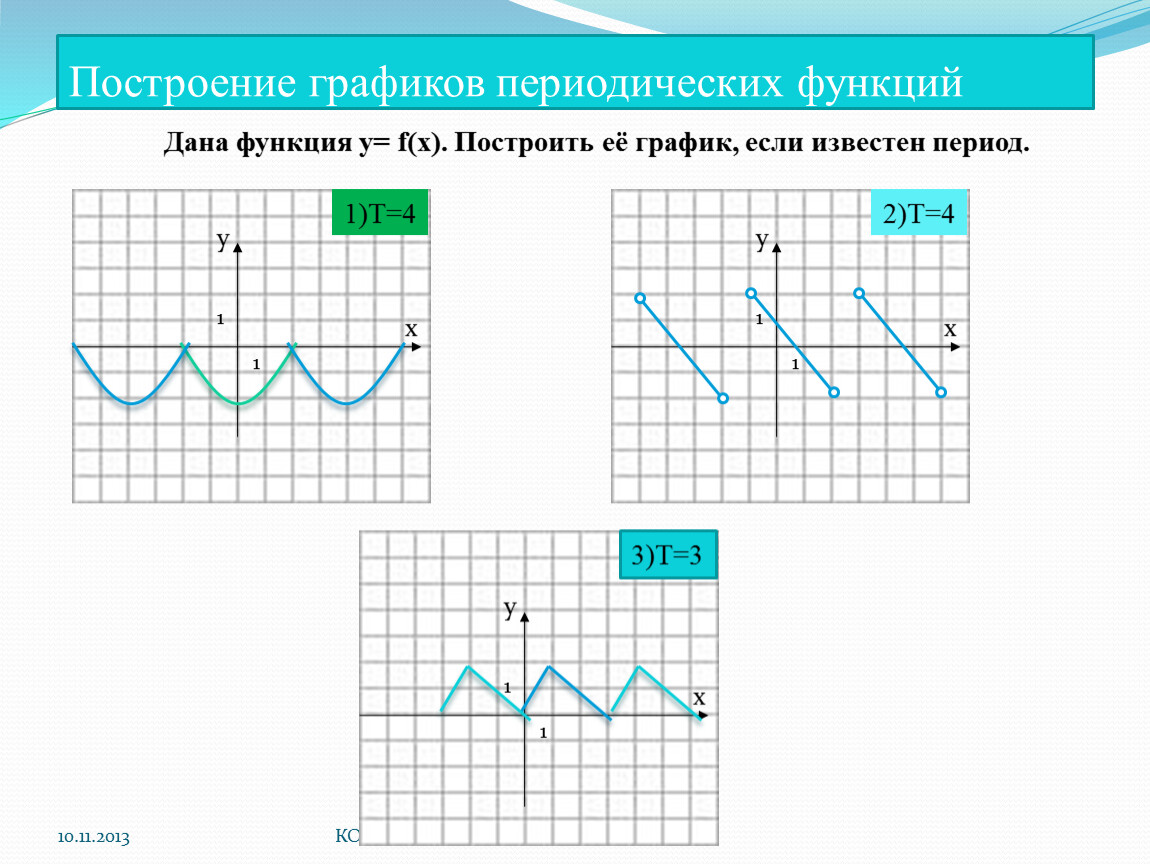
При построении графиков важно учитывать знаки коэффициентов, так как они могут инвертировать график или изменять его направление.

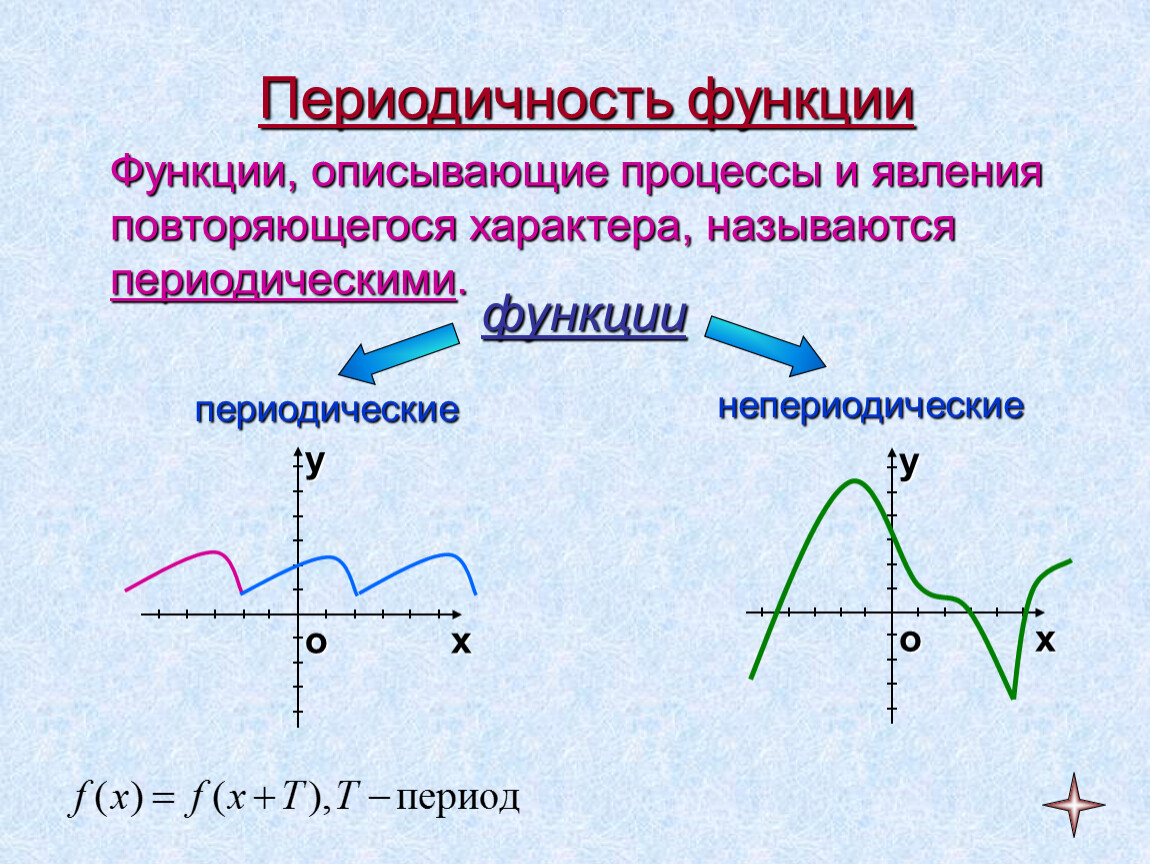
Периодические функции
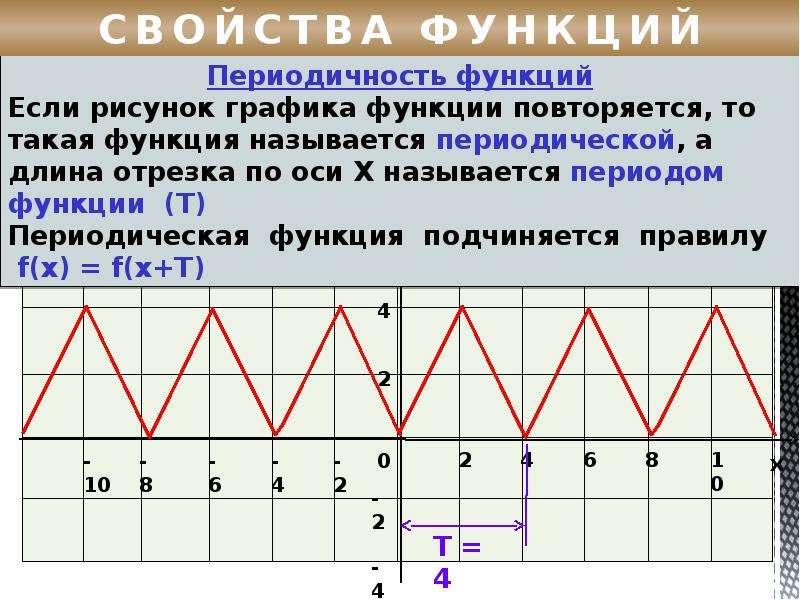
Часто для простоты восприятия функции представляют в виде линейных или степенных преобразований для их графического отображения.

Построение графиков тригонометрических функций с помощью преобразований. Практ. часть. 10 класс.
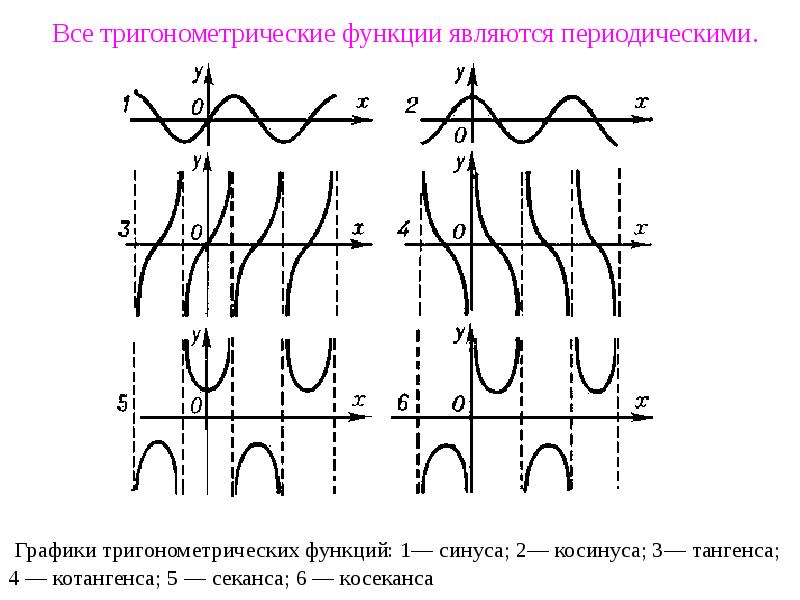
При решении задач по графикам периодических функций всегда проверяйте, не перепутаны ли значения периода и амплитуды.

Свойства функции. Периодичность. 10 класс.
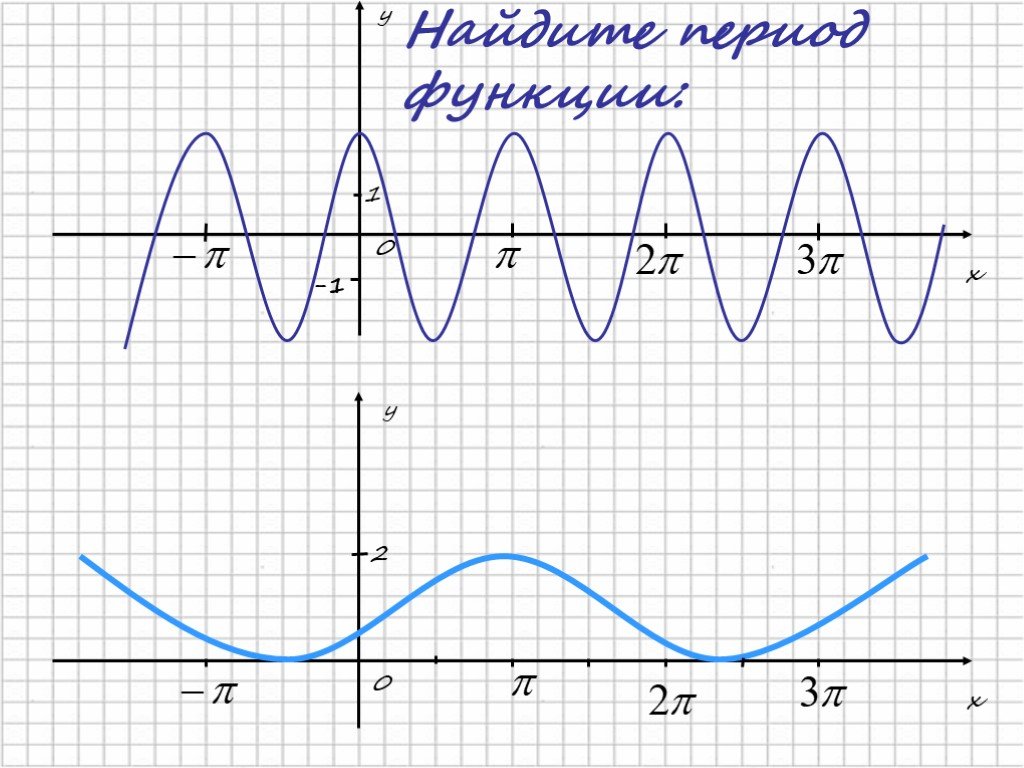
Регулярно практикуйтесь в рисовании графиков с разными значениями параметров для лучшего освоения материала.

Вебинар 11. Параметр. Периодичность функций
