Когда функция дифференцируема на интервале: основные признаки и их значение
Дифференцируемость функции на интервале является важным свойством, которое влияет на её поведение и характеристики. Чтобы функция была дифференцируемой на интервале, необходимо, чтобы в каждой точке интервала существовала её производная. Этот критерий тесно связан с непрерывностью функции, однако наличие непрерывности не всегда означает дифференцируемость. Разберёмся в том, как проверяется дифференцируемость и что это даёт в практическом применении.
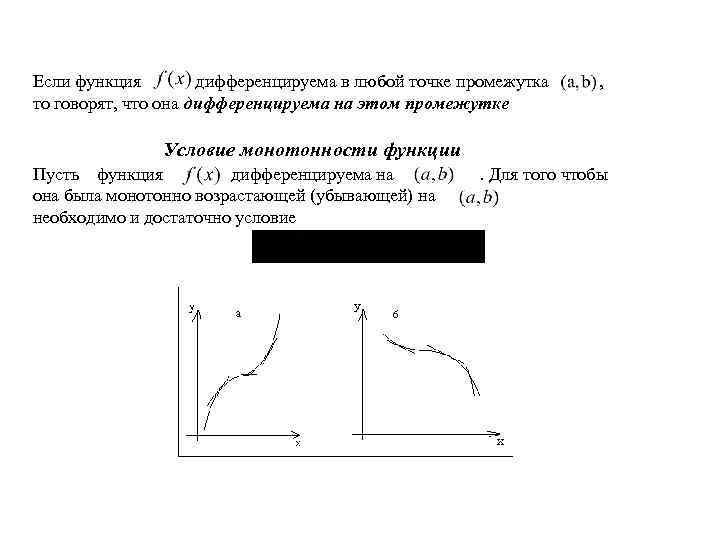

Для того чтобы функция была дифференцируемой на интервале, она должна быть непрерывной на этом интервале, но не всякая непрерывная функция обязательно дифференцируема.

Математический анализ, 12 урок, Монотонность и экстремумы функции
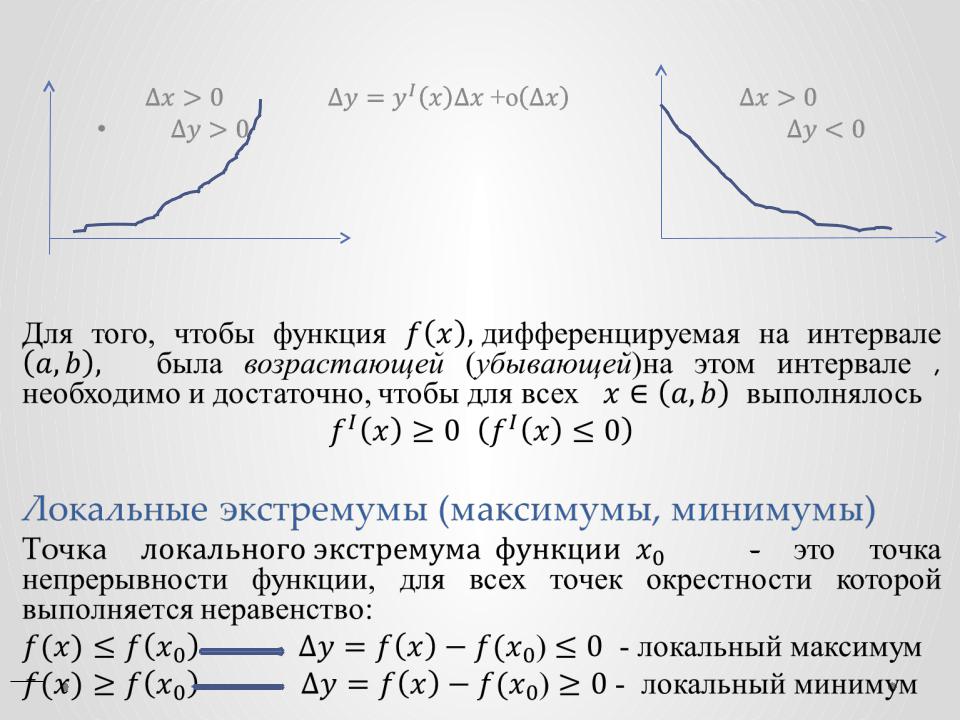

Если производная функции существует в каждой точке интервала, это означает, что функция не имеет прыжков или разрывов на данном интервале.

✓ Дифференцируемая функция. Дифференциал - матан #032 - Борис Трушин

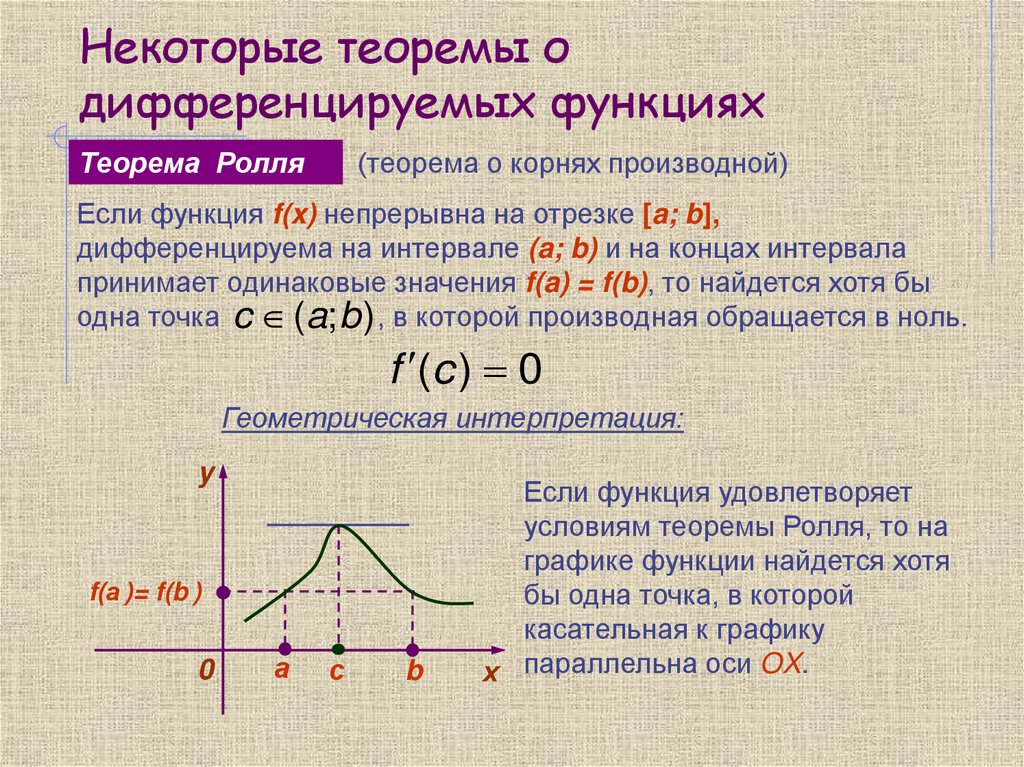
Для проверки дифференцируемости функции на интервале полезно использовать критерий Ролля или критерий Лагранжа, которые позволяют устанавливать связь между значениями функции и её производной.
21. Дифференциал функции


Если функция не дифференцируема в точке, это может указывать на наличие углов, вертикальных касательных или разрывов на графике функции.

Пример всюду непрерывной, но нигде не дифференцируемой функции
Важным практическим советом является использование производных для нахождения экстремумов функции — максимумов и минимумов — на интервале.

Исследование функции на дифференцируемость (часть 1)

Если функция имеет производную в каждой точке интервала, это гарантирует её гладкость и отсутствие изломов на графике.
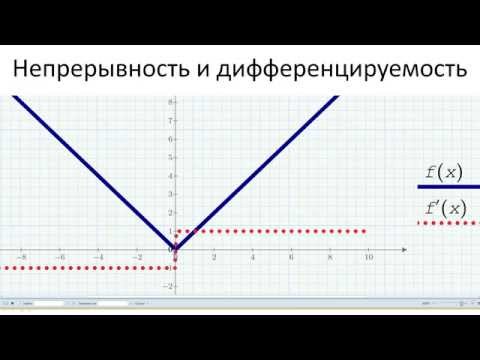
likerkacinema.ru дифференцируемости и непрерывности
Для функций, представленных на отрезке, важно учитывать и левую, и правую производную в граничных точках, чтобы удостовериться в дифференцируемости на всём интервале.

Для более сложных функций можно использовать численные методы, такие как численное дифференцирование, чтобы проверить их дифференцируемость на интервале.

Шапошников С. В. - Математический анализ II - Дифференцируемые функции

Если график функции имеет резкие повороты или вертикальные касательные, это сигнализирует о том, что функция не дифференцируема в соответствующих точках.

Дифференцируемость функции одной переменной.


Важно помнить, что для функции, которая дифференцируема на интервале, производная будет непрерывной, что является её дополнительным свойством.


Функция достигает наименьшего и наибольшего значения на интервале РЭШ