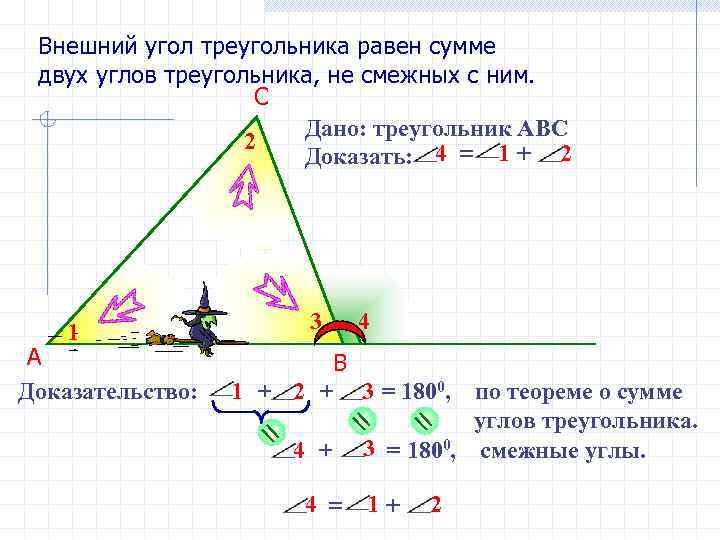
Внешние углы треугольника: важные особенности и полезные факты
Если у треугольника внешние углы равны, это может существенно повлиять на его свойства и характеристики. Важно понимать, как такие углы соотносятся с внутренними и как они помогают решить задачи по геометрии. В этой статье мы собрали несколько полезных советов и рекомендаций для тех, кто сталкивается с такими треугольниками.
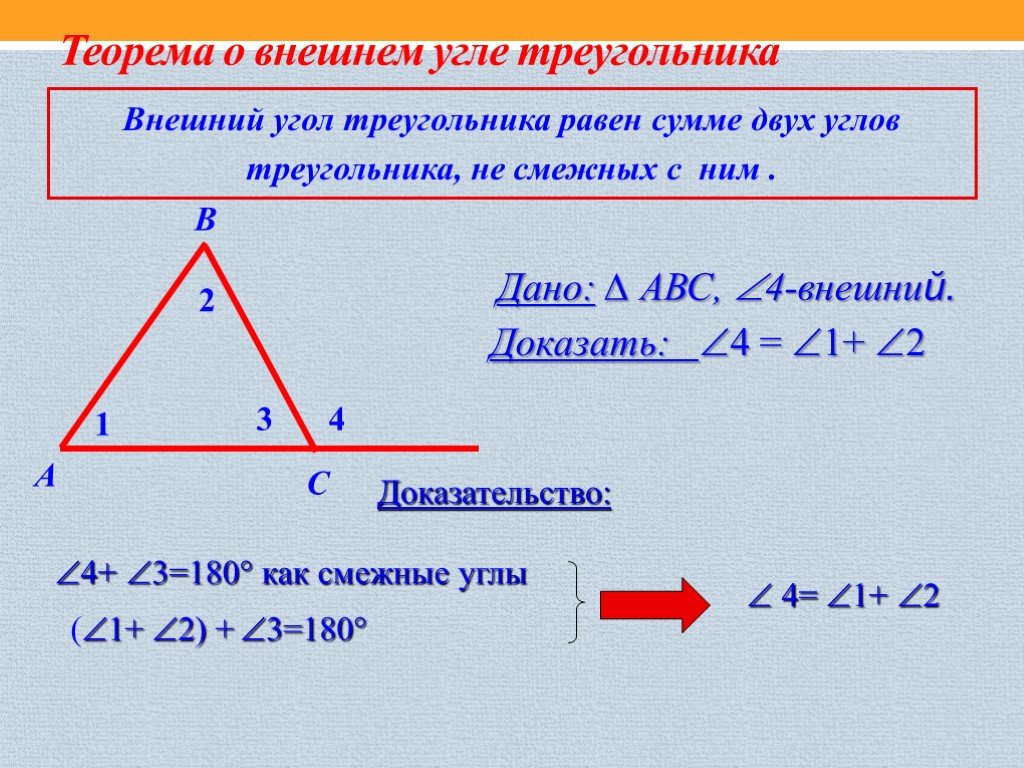


Для треугольников с равными внешними углами важно помнить, что их сумма всегда будет равна 360 градусам.

Внешний угол треугольника
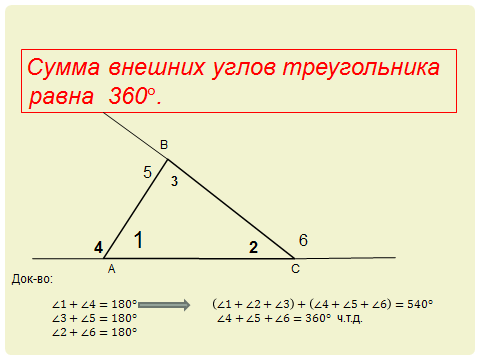
Если два внешних угла равны, это может свидетельствовать о том, что треугольник имеет специфические симметричные свойства.

Внешний угол треугольника
Внешние углы треугольника связаны с его внутренними углами через формулу: внешний угол = 180° - внутренний угол.

ВНЕШНИЕ УГЛЫ ТРЕУГОЛЬНИКА 😉 #shorts #математика #егэ #огэ #профильныйегэ
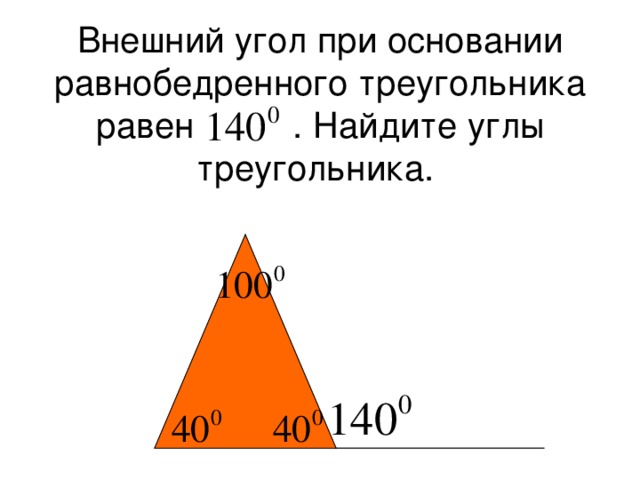
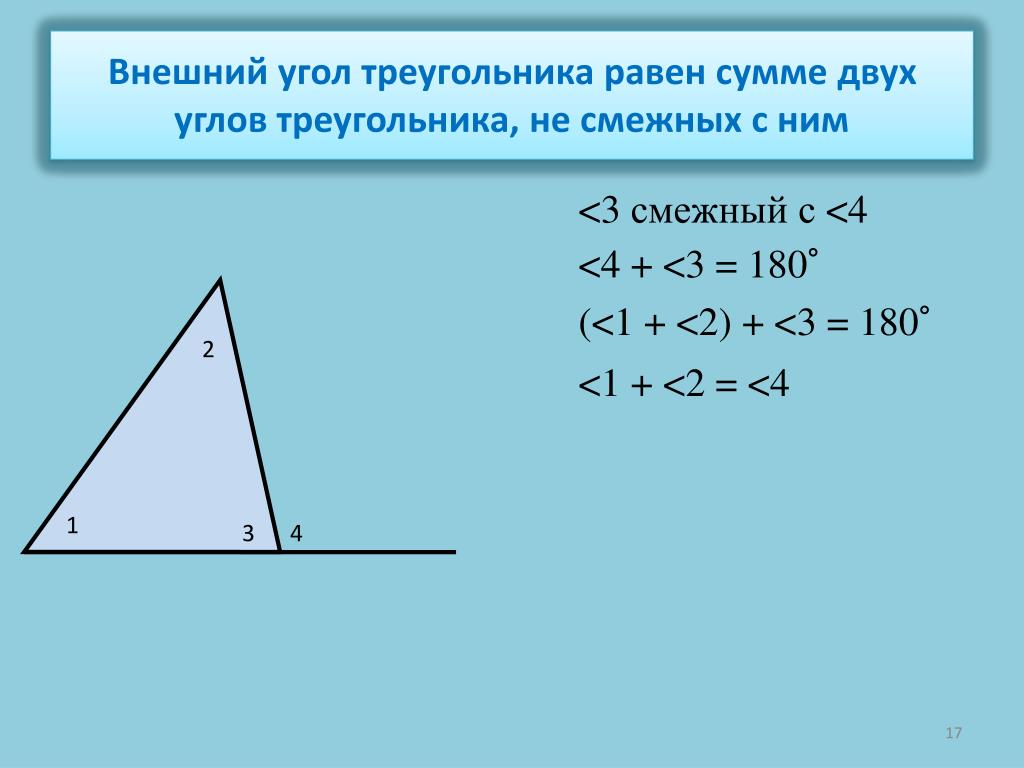
Внимательно проверьте все углы в треугольнике перед тем, как использовать теорему о внешних углах, чтобы избежать ошибок.

Классный способ для разметки любого угла без транспортира.
Если у треугольника равные внешние углы, это может указать на наличие равнобедренности, то есть два его внутренних угла будут равны.

Внешний угол треугольника

Такой треугольник можно использовать для задач, связанных с симметрией и геометрическими построениями, где равенство углов помогает упростить решение.

При решении задач по треугольникам с одинаковыми внешними углами, обращайте внимание на их взаимосвязь с другими геометрическими фигурами, такими как многоугольники.

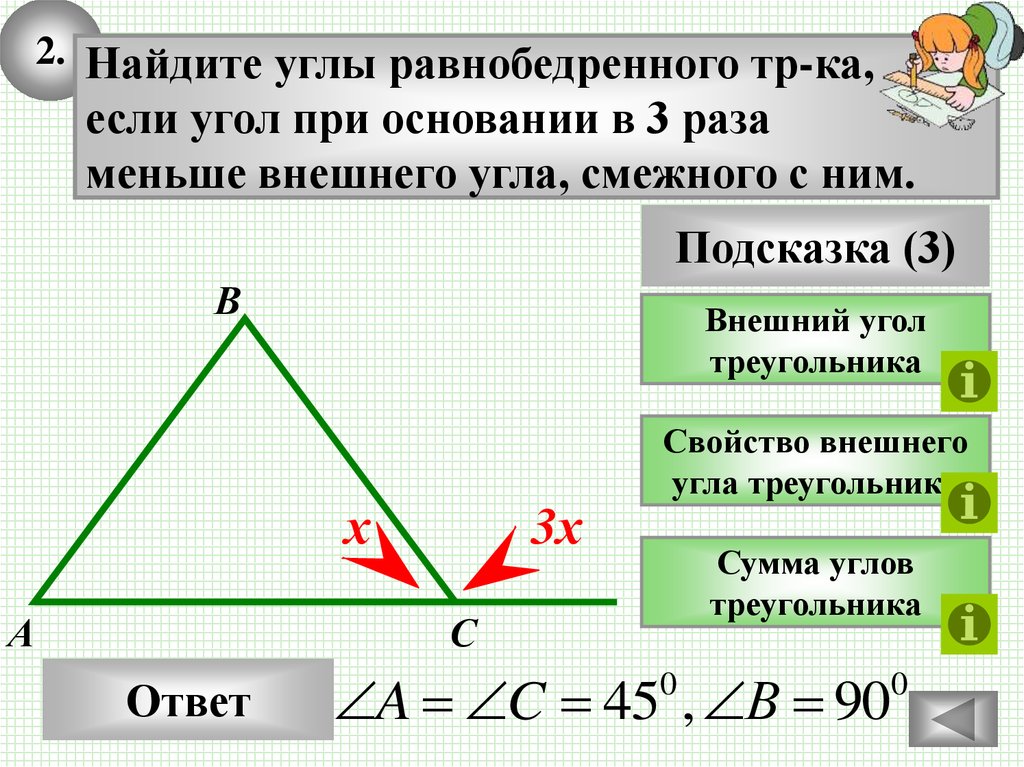
Не забывайте, что равенство внешних углов треугольника — это не обязательное, а возможное условие, которое открывает дополнительные возможности для анализа.
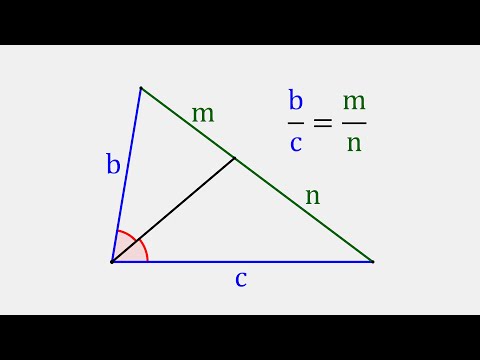
Свойство (признак) биссектрисы внутреннего (внешнего) угла треугольника

Для уточнения свойств треугольника с равными внешними углами можно использовать дополнительные теоремы, такие как теорема о внешних углах многоугольников.

⚠️🔺Геометрический Секрет Треугольника: Почему внешний угол равен сумме двух несмежных углов?

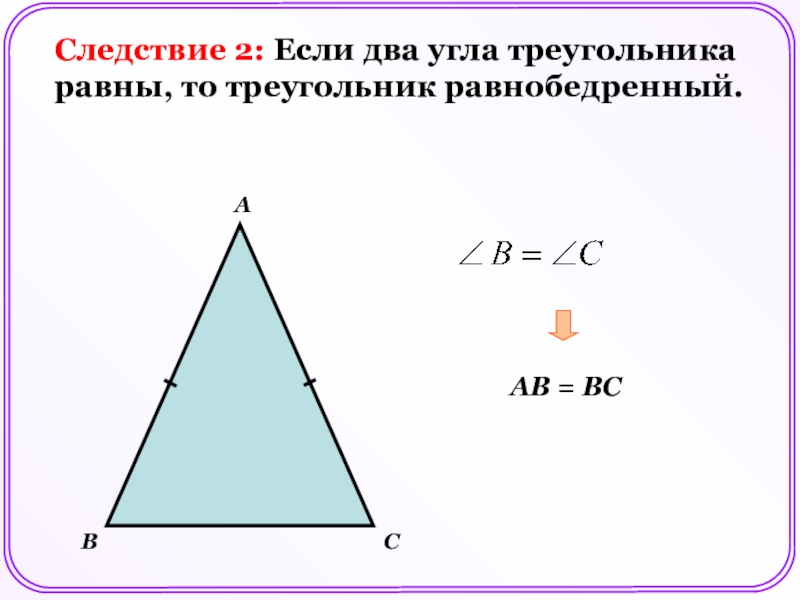
При изучении треугольников с одинаковыми внешними углами полезно также обратить внимание на их применение в реальных задачах, например, в инженерии или архитектуре.