Что делать, если в квадратном уравнении коэффициент при x равен нулю
В данном разделе рассматриваются способы решения квадратных уравнений, где коэффициент при x равен нулю, а также возможные варианты их упрощения и анализа. Мы подробно расскажем о том, как такие уравнения могут быть преобразованы в линейные, и какие шаги нужно предпринять для их решения.

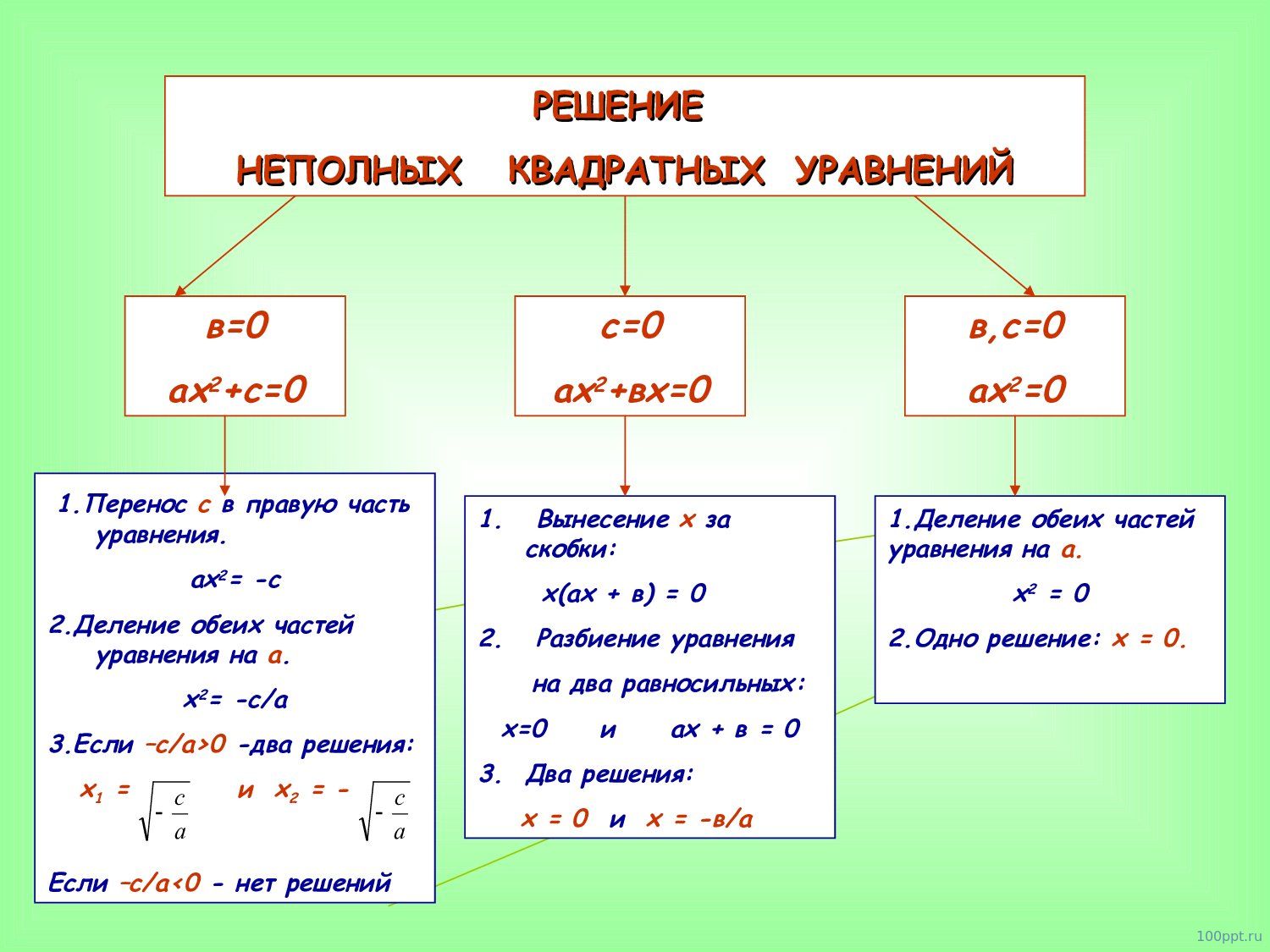
Если коэффициент при x равен нулю, то уравнение становится линейным и его можно решить методом подбора или с использованием формулы для линейных уравнений.

За халявой переходи в шапку профиля #огэ #онлайншкола #математика #егэ

Когда a = 0, уравнение теряет квадратный член, и получается выражение вида bx + c = 0, которое решается по стандартной формуле x = -c / b.

МАТЕМАТИКА 8 класс - Неполные Квадратные Уравнения. Как решать Неполные Квадратные Уравнения?

Если у вас есть уравнение вида 0x² + bx + c = 0, то его решение сводится к нахождению x через b и c, так как нет квадратного члена.

Решение квадратного уравнения 9х²–6х+1=0 (D=0)


Для уравнений с a = 0, важно помнить, что если b = 0, то уравнение не имеет решений, а если c = 0, то решений бесконечно много.

АЛГЕБРА 8 класс : Решение неполных квадратных уравнений - Видеоурок
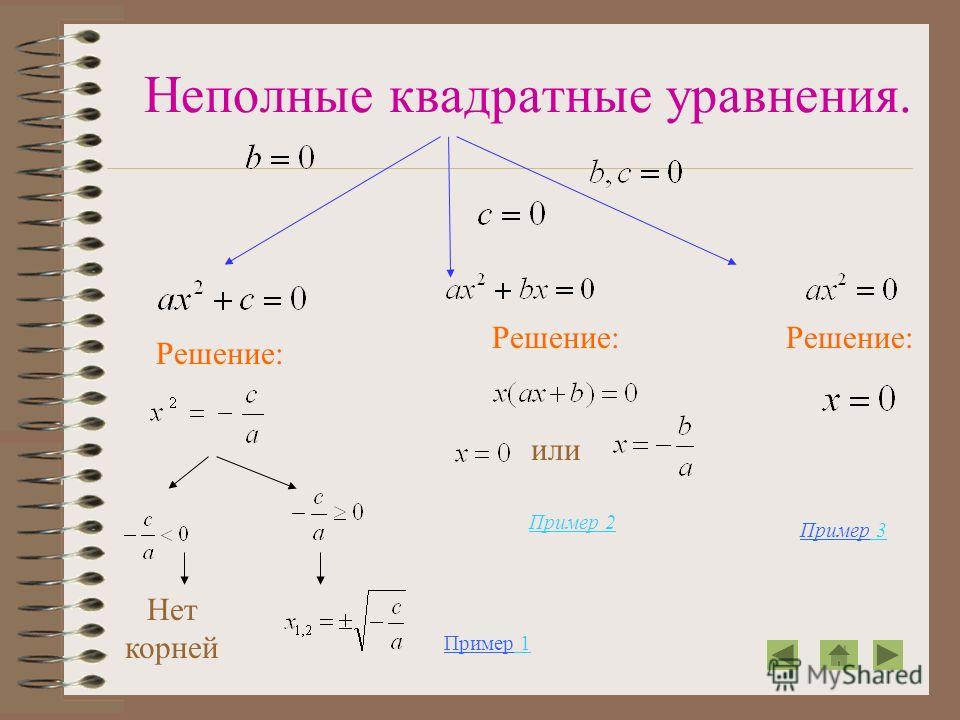
Если уравнение имеет вид 0x² + bх = -c, то оно сводится к линейному уравнению, решение которого можно легко найти, деля обе стороны на b.
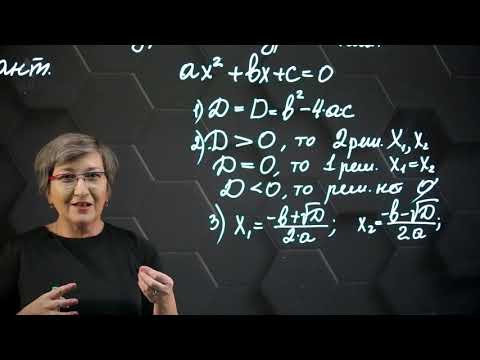
Решение квадратных уравнений. Дискриминант. 8 класс.


При решении уравнений с нулевым коэффициентом квадратичного члена важно внимательно относиться к знакам, так как от них зависит наличие или отсутствие решений.
Если коэффициент при x равен нулю, проверьте, не содержит ли уравнение других особенностей, таких как отсутствие решений или бесконечное количество корней.
Не забывайте, что уравнение 0x² + bx = c имеет одно решение, если b не равно нулю и c делится на b без остатка.

При отсутствии квадратного члена важно обращать внимание на знаки других коэффициентов, так как это влияет на интерпретацию корней уравнения.


Решение уравнений с нулевым коэффициентом квадратичного члена часто бывает проще, но требует внимательности, чтобы избежать ошибок в вычислениях.

Неполные квадратные уравнения. Алгебра, 8 класс
