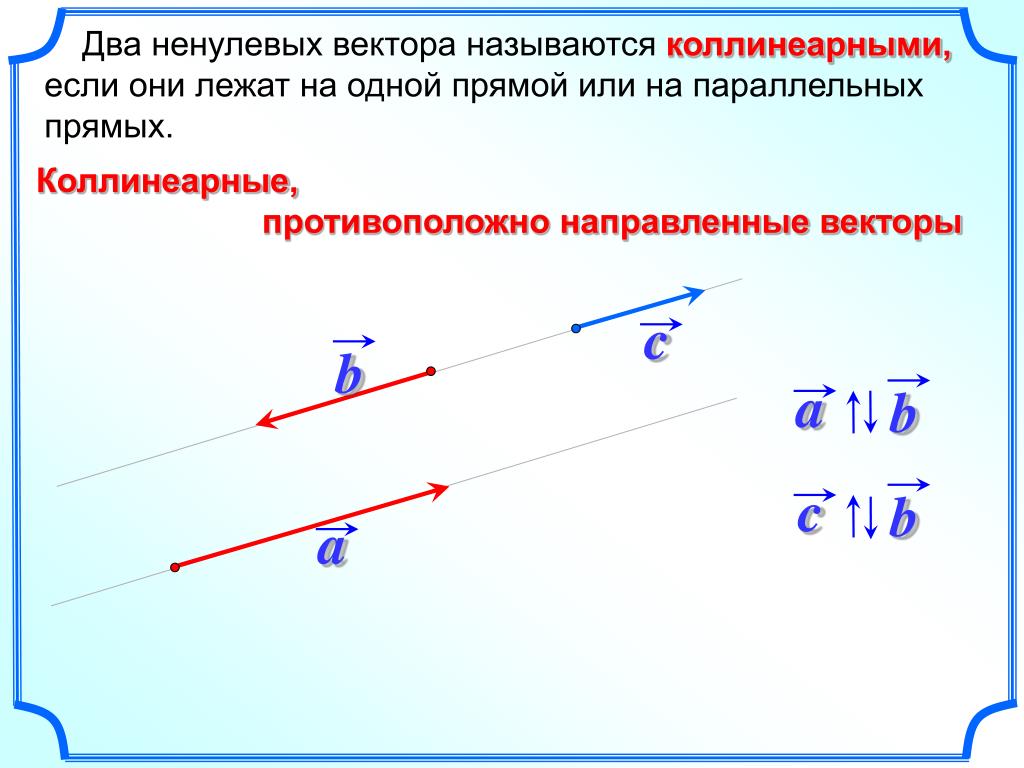
Что значит, что два вектора равны? Полное объяснение и примеры
Равенство векторов — один из фундаментальных принципов векторной алгебры. Векторы считаются равными, если они имеют одинаковую длину и направлены в одну и ту же сторону. Важно помнить, что равенство векторов зависит не только от их координат, но и от направления. В этом разделе вы найдете объяснения, примеры и полезные советы по работе с векторами.
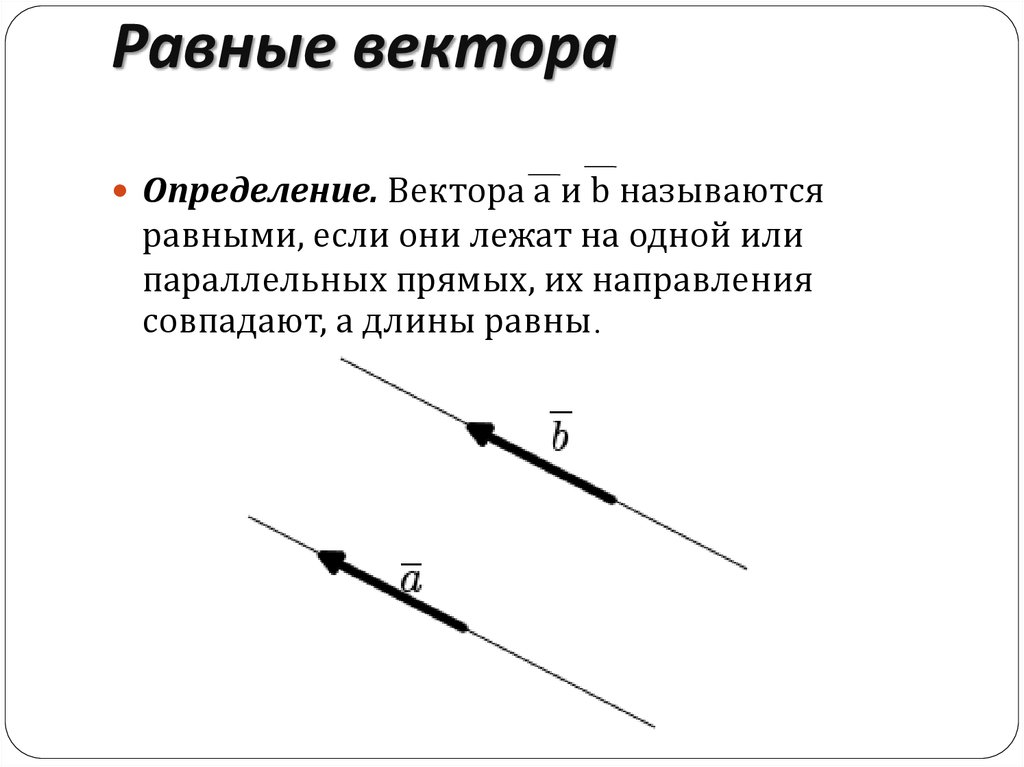
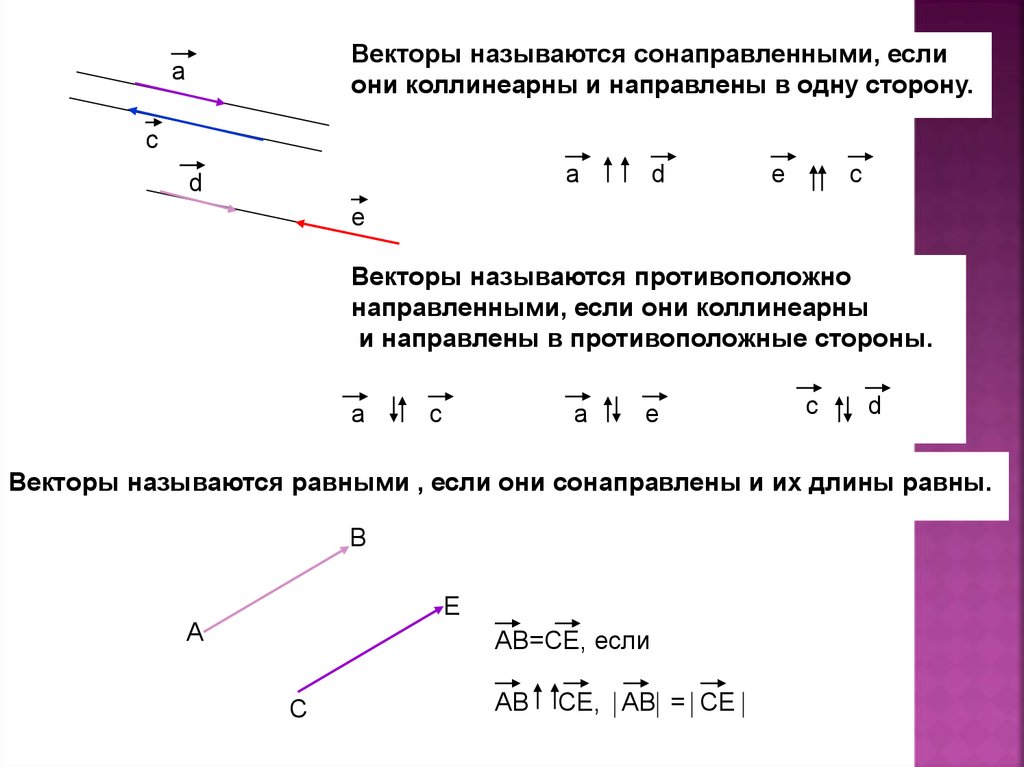

При сравнении векторов важно учитывать их направление и длину, а не только координаты.

Вектор. Определение. Коллинеарные векторы. Равные векторы.
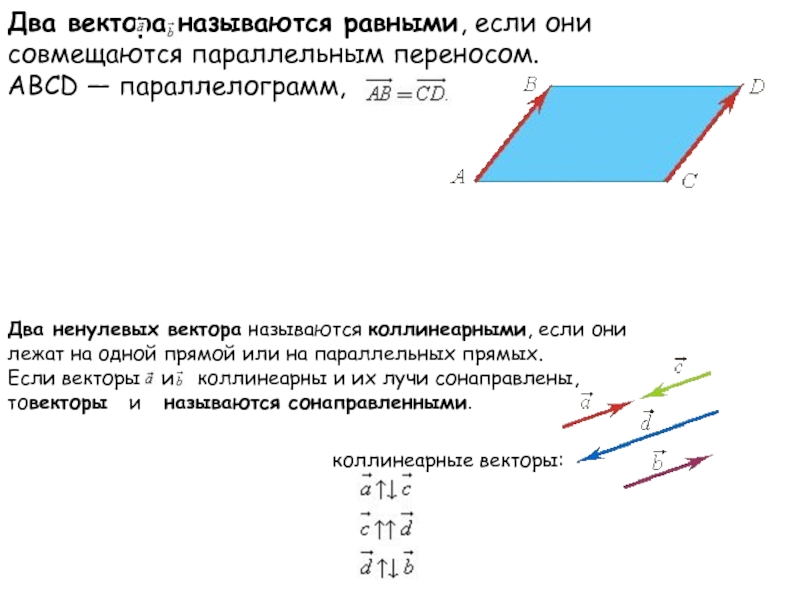
Чтобы проверить равенство двух векторов, сравните их компоненты по каждому из направлений.

ПРОСТОЙ СПОСОБ, как запомнить Векторы за 10 минут! (вы будете в шоке)
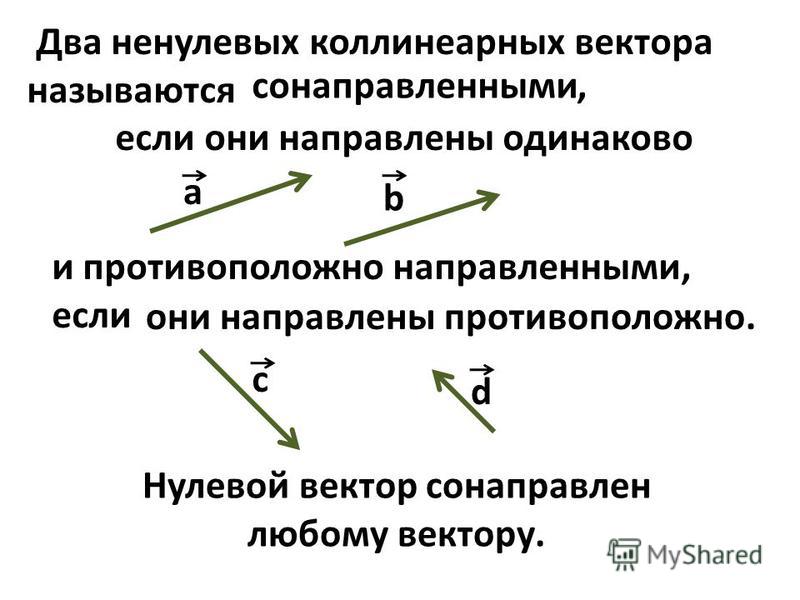
Используйте графическое изображение векторов для наглядности: это помогает легче понять их равенство.

Коллинеарные векторы. Равные векторы
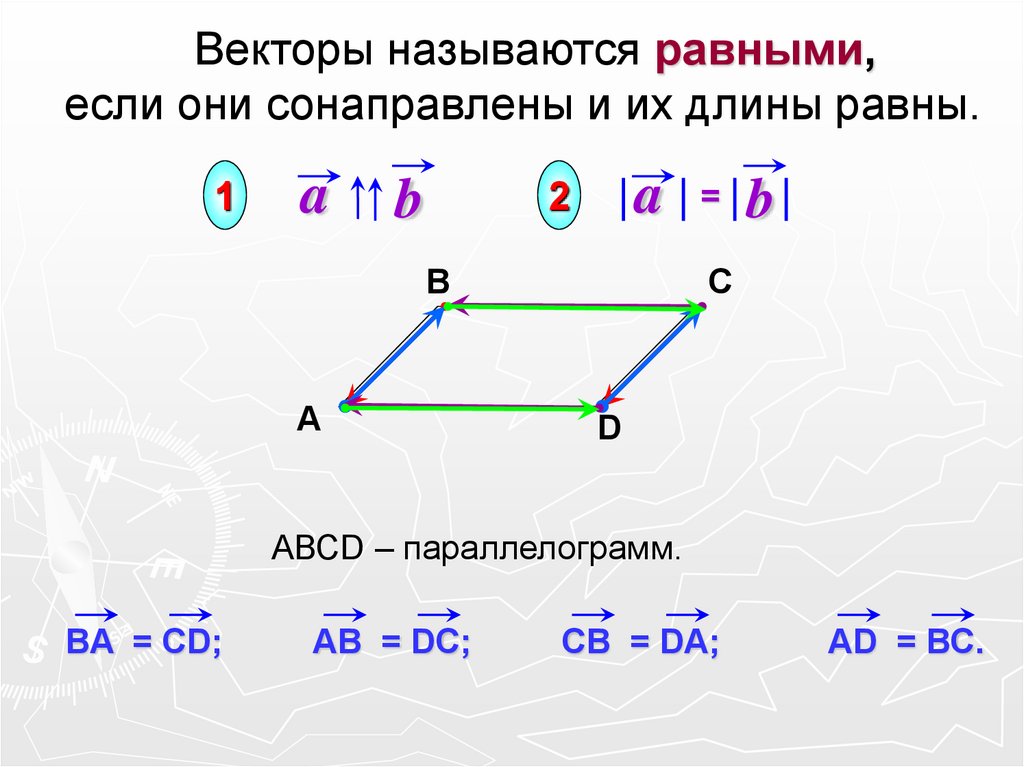

Векторы, равные по длине и направлению, могут быть представлены различными способами, но их свойства останутся одинаковыми.

Равные векторы в пространстве. Коллинеарные векторы.

Помните, что равенство векторов — это не просто совпадение координат, а полное совпадение всех характеристик.

ВСЕ ПРО ВЕКТОРА - НОВОЕ ЗАДАНИЕ ЕГЭ по Профилю (Номер 2)


Если векторы равны, то они могут быть приведены друг к другу с помощью параллельного переноса.

Равенство векторов. 9 класс.

Не забывайте о том, что если два вектора равны, то их компоненты должны быть пропорциональны.

Вектор в пространстве
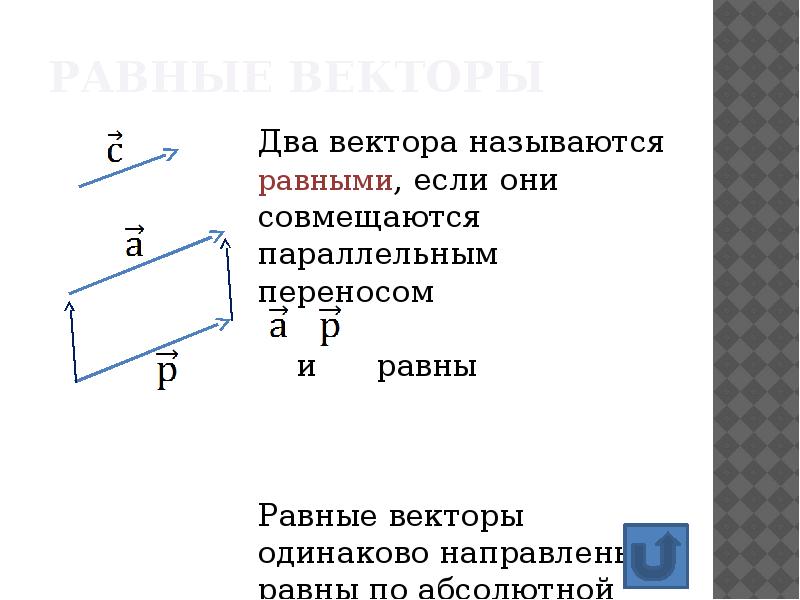
Для практической проверки равенства векторов можно воспользоваться формулами длины и угла между ними.
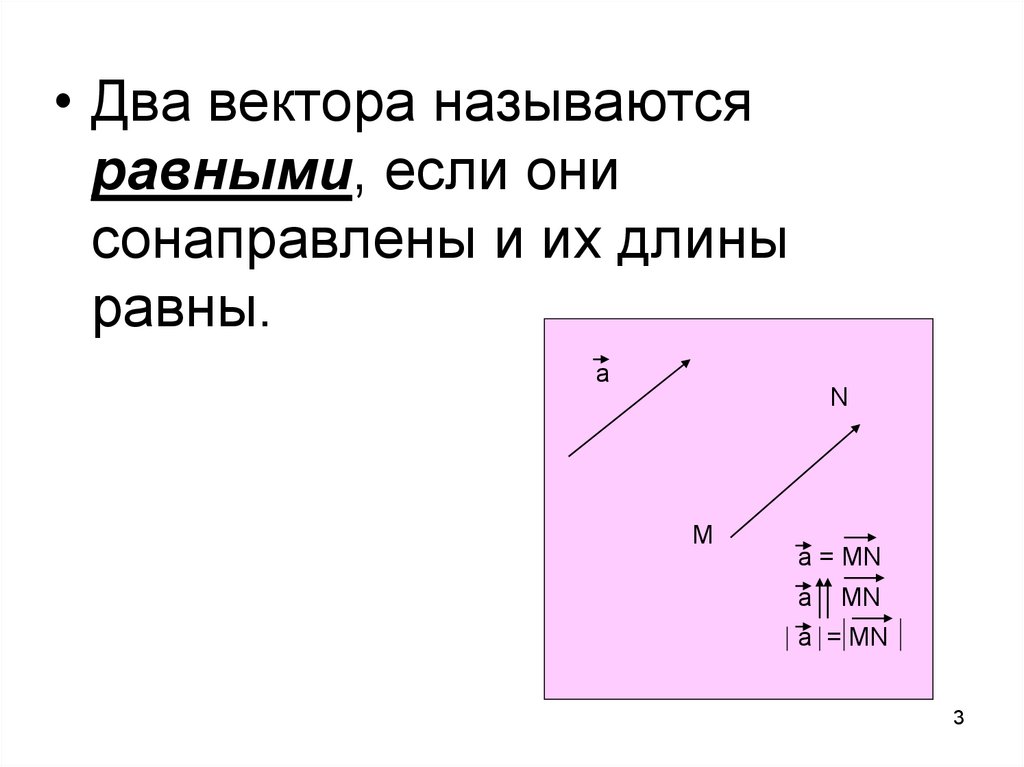

Сравнивая векторы в разных системах координат, важно удостовериться, что системы находятся в одинаковом положении.


Практикуйтесь с различными задачами на равенство векторов, чтобы лучше понять этот важный математический принцип.