Основные аспекты дисперсии нормального распределения и ее влияние на статистику

Дисперсия нормального распределения играет ключевую роль в анализе статистических данных, так как она определяет степень разброса значений вокруг среднего. На этой странице мы собрали полезные советы, которые помогут вам лучше понять, как вычислять и интерпретировать дисперсию в рамках нормального распределения, а также научиться правильно использовать этот показатель в различных статистических задачах.

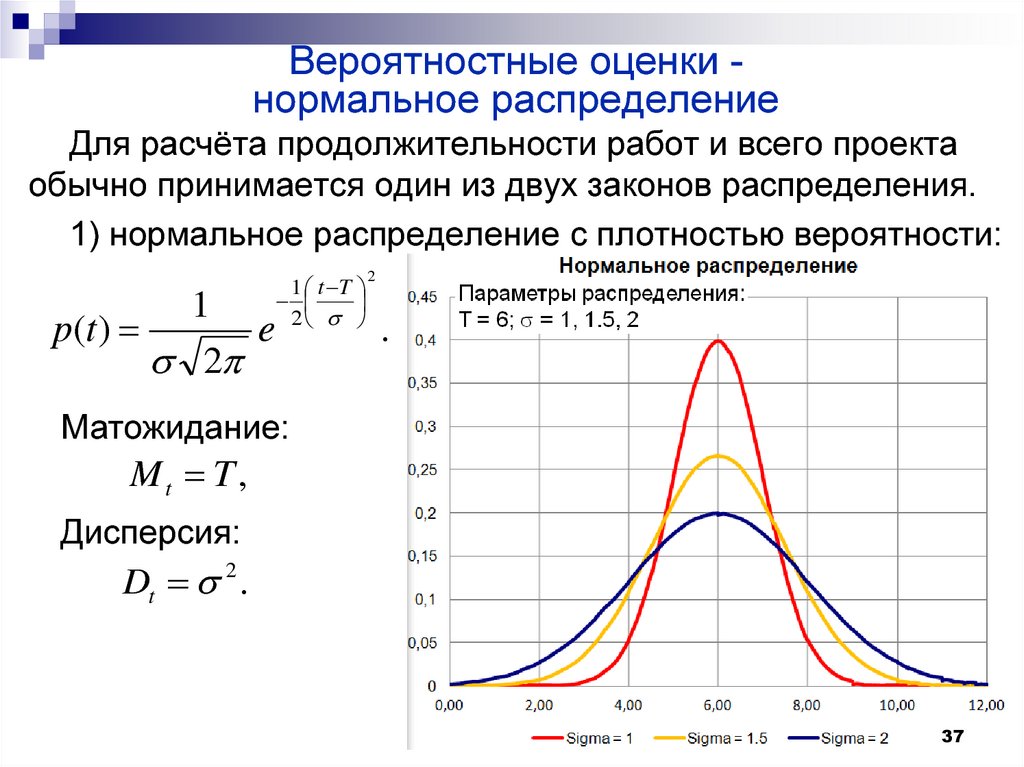
Для вычисления дисперсии нормального распределения необходимо сначала найти квадрат отклонений от среднего значения для каждого наблюдения, а затем усреднить эти квадраты. Это и будет дисперсия.

Высокая дисперсия указывает на значительный разброс данных вокруг среднего значения, в то время как низкая дисперсия свидетельствует о большей концентрации значений вблизи среднего.

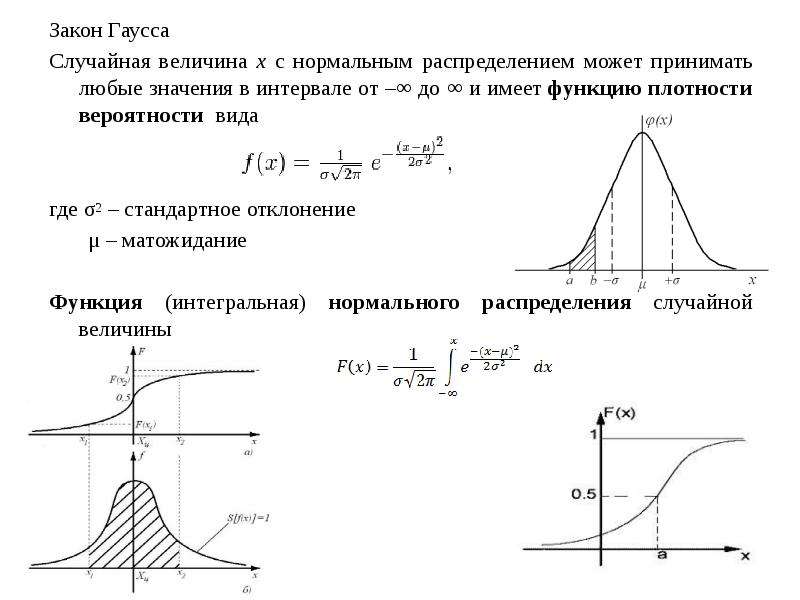
Важно помнить, что для нормального распределения стандартное отклонение является квадратным корнем из дисперсии, что позволяет легко оценить степень разброса данных.

Для улучшения точности расчётов при вычислении дисперсии используйте выборочную дисперсию, особенно когда работаешь с выборкой данных, а не с генеральной совокупностью.

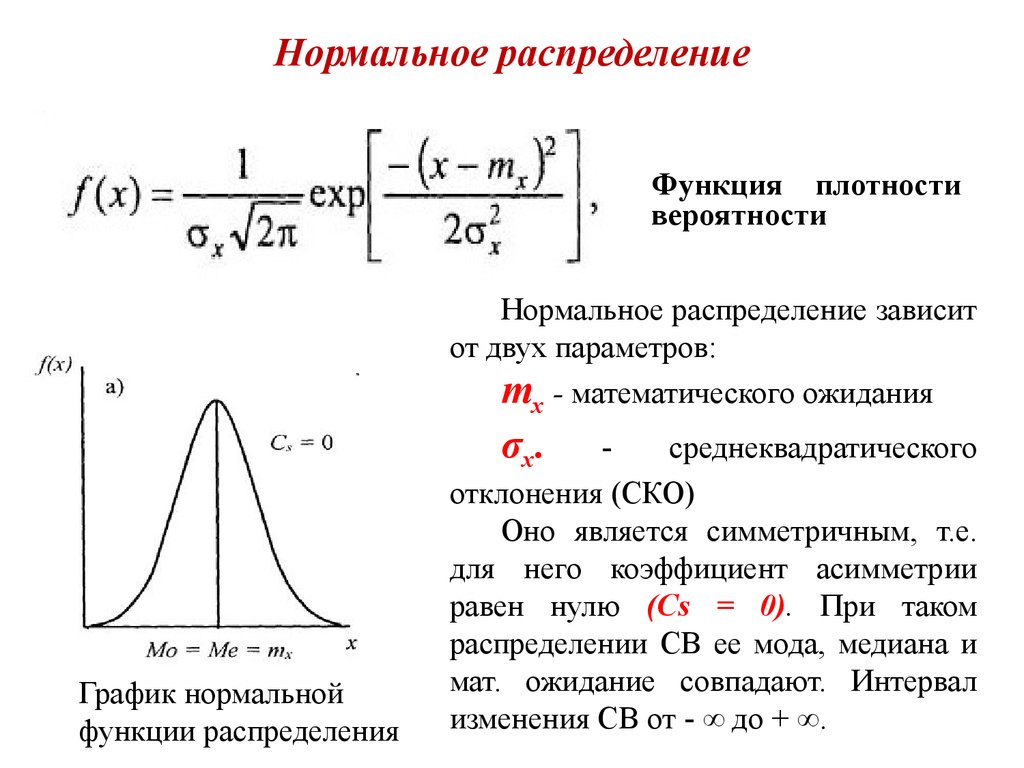
Если данные имеют сильные выбросы, это может существенно повысить дисперсию, поэтому перед анализом стоит оценить влияние экстремальных значений на результаты.

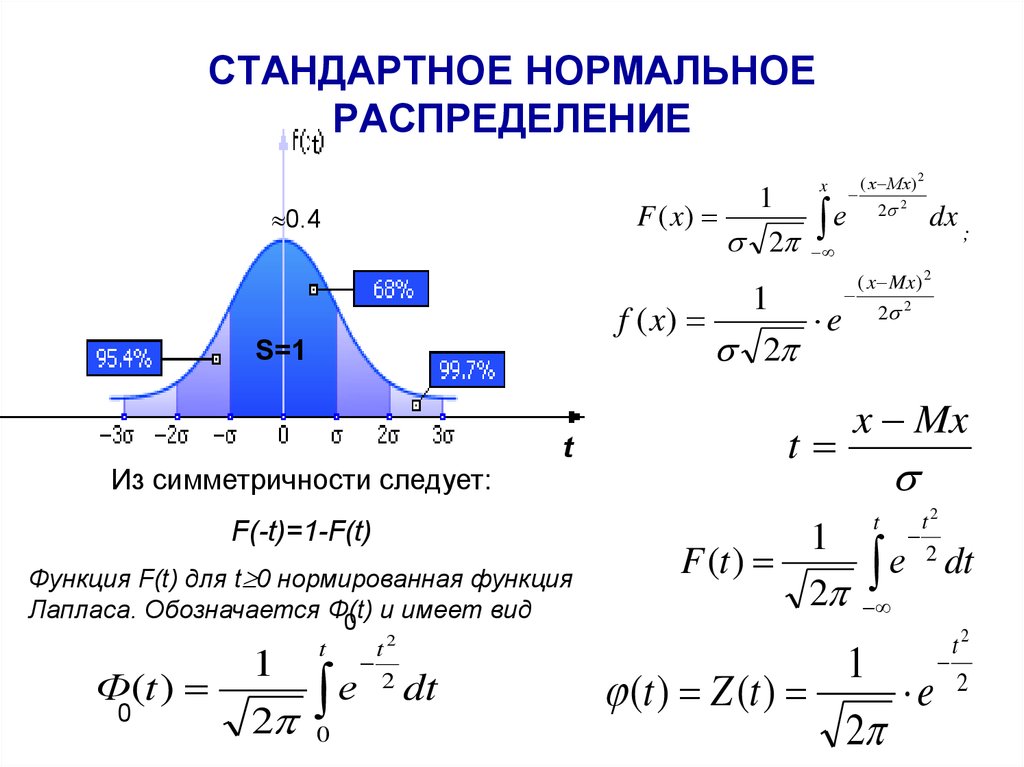
Для того чтобы визуализировать данные и лучше понять их распределение, полезно построить график распределения, например, гистограмму, с наложением кривой нормального распределения.

Если вы работаете с большим объемом данных, использование специализированных статистических пакетов, таких как R или Python, значительно ускорит расчёты и упростит анализ.

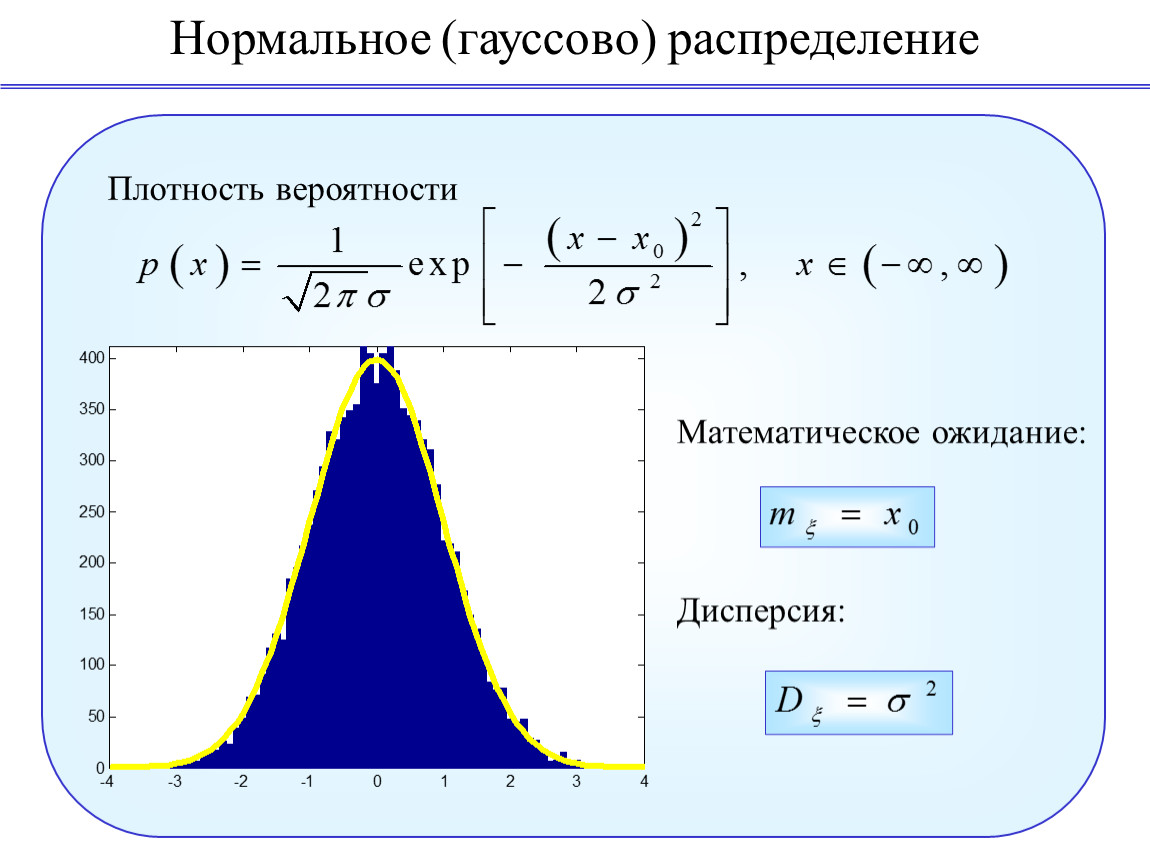
Помимо дисперсии, следует учитывать другие меры рассеяния, такие как интерквартильный размах и коэффициент вариации, для более глубокой оценки разброса данных.

При анализе статистики важно учитывать контекст данных, так как высокая дисперсия может быть как признаком разнообразия, так и следствием ошибок в сборе данных.

Нормальное распределение, как правило, предполагает симметричность и отсутствие сильно выраженных отклонений, однако важно проверять на наличие таких отклонений для корректной интерпретации дисперсии.